С помощью дифференциального исчисления можно установить характерные особенности изменения функций: возрастание и убывание, максимумы и минимумы, направление вогнутости графика, наличие асимптот. Обычно используют следующую схему исследования функций:
- Определение области определения.
- Определение четности или нечетности.
- Определение периодичности функции.
- Определение интервалов знака постоянства первой производной.
- Определение интервалов знака постоянства второй производной.
- Составление таблицы результатов.
| х | |||||||
| у ' | |||||||
| у '' | |||||||
| у |
- В первой строчке таблицы указываются интервалы, на которые разбивается область определения функции точками разрыва, точками экстремума и точками перегиба в порядке следования. Сами эти точки в порядке следования помещаются в отдельные столбцы. Во второй строчке таблицы в каждой ячейке указываются знаки первой производной. В третьей строчке таблицы в каждой ячейке указываются знаки второй производной. В четвёртой строчке определяется характер поведения функции в каждой ячейке. Если это точки экстремума или точки перегиба, то указываются значения функции в этих точках.
- Нахождение асимптот.
- Построение графика функции, начинается с построения асимптот и характерных точек.
Полное исследование функций и построение их графиков удобно выполнять по следующей схеме.
1) найти область определения функции;
2) выяснить, не является ли функция чётной или нечётной, периодической;
3) исследовать непрерывность, найти точки разрыва и выяснить характер разрывов;
4) найти асимптоты графика функции;
5) исследовать монотонность функции и найти ее экстремумы;
6) найти точки перегиба, установить интервалы выпуклости и вогнутости графика функции;
7) обозначить дополнительные точки графика функции, например, точки его пересечения с осями координат.
12. Понятие первообразной. Неопределенный интеграл, свойства и основные методы интегрирования.
1. Понятие первообразной функции. Свойства первообразной
Во многих вопросах науки и техники возникает необходимость восстанавливать функцию по ее известной производной.
Будем говорить, что функция  в интервале
в интервале  называется первообразной функцией для функции
называется первообразной функцией для функции  , если
, если
 . (1.1)
. (1.1)
Пусть  — первообразная для
— первообразная для  , тогда любая функция
, тогда любая функция  , где
, где  , также будет первообразной для
, также будет первообразной для  . Действительно,
. Действительно,
 .
.
Таким образом, если функция имеет первообразную, то она имеет бесконечное множество первообразных.
Теорема 1. Любые две первообразные функции  отличаются на постоянную.
отличаются на постоянную.
Доказательство. Пусть  и
и  - первообразные для
- первообразные для  . Это означает, что
. Это означает, что
 и
и 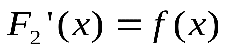 для
для 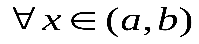 .
.
Рассмотрим функцию  . Для нее
. Для нее
 .
.
Везде дальше произвольную постоянную будем обозначать  .
.
2. Понятие неопределенного интеграла, свойства неопределенного интеграла
Определение 1. Пусть функция  определена на
определена на  . Множество всех первообразных для функции
. Множество всех первообразных для функции  называется неопределенным интегралом для
называется неопределенным интегралом для  и обозначается
и обозначается  (при этом
(при этом  называется подинтегральным выражением):
называется подинтегральным выражением):
 ,
,
где  — одна из первообразных функции
— одна из первообразных функции  ,
,  .
.
Равенство интегралов
 =
= 
понимается как равенство множеств первообразных.
Пусть функции  ,
,  ,
,  определены на
определены на  , а
, а  ,
,  ,
,  — их соответствующие первообразные на
— их соответствующие первообразные на  . Через
. Через  будем обозначать дифференциалы соответствующих функций. Тогда
будем обозначать дифференциалы соответствующих функций. Тогда
-
 ;
;
-
 ;
;
-
 , де
, де  ;
;
-
 .
.
Докажем свойство 4:

13. Определенный интеграл и его свойства. Формула Ньютона-Лейбница.
1. Понятие определенного интеграла
Пусть функция  определена на отрезке
определена на отрезке  . Разобьем отрезок
. Разобьем отрезок  на
на  частей точками
частей точками  . Выберем на каждом из полученных отрезков
. Выберем на каждом из полученных отрезков  произвольную точку
произвольную точку  .
.
Интегральной суммой функции  на отрезке
на отрезке  называется сумма
называется сумма
 или
или
 , где
, где  .
.
Наибольшую из длин  обозначим через
обозначим через 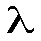 .
.

Определенным интегралом функции  на отрезке
на отрезке  называется число, равное пределу интегральной суммы
называется число, равное пределу интегральной суммы  и обозначается
и обозначается  , т.е.
, т.е.
 .
.
Из условия  следует, что
следует, что  .
.
Пределами интегрирования называются числа  и
и  .
.
Подынтегральной функцией называется функция  .
.
Если функция  непрерывна на отрезке
непрерывна на отрезке  , то определенный интеграл
, то определенный интеграл  существует.
существует.
Подчеркнем, что определенный и неопределенный интегралы существенно различаются между собой. Если неопределенный интеграл представляет семейство функций, то определенный - есть определенное число.
2. Свойства определенного интеграла
1. Постоянный множитель можно выносить за знак интеграла
 .
.
2. Интеграл от алгебраической суммы двух функций равен сумме интегралов от этих функций (верно для любого числа слагаемых):
 .
.
3. При перемене порядка интегрирования знак определенного интеграла меняется на противоположный:
 .
.
4. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых а, b и с справедливо
 .
.
5. Обе части неравенства можно почленно интегрировать, т.е. если для всех 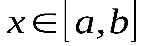
 , то
, то
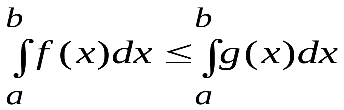 .
.
6. Для  определенный интеграл
определенный интеграл  становится функцией от переменного верхнего предела
становится функцией от переменного верхнего предела  . Производная этой функции равна значению подынтегральной функции в точке
. Производная этой функции равна значению подынтегральной функции в точке  :
:
 .
.
7. Теорема о среднем. Если функция  непрерывна на
непрерывна на  , то существует точка
, то существует точка  такая, что
такая, что
 .
.
Значение  называется средним значением функции
называется средним значением функции  на
на  .
.
 у
у 
В

А




Площадь криволинейной трапеции  равна площади прямоугольника с основанием
равна площади прямоугольника с основанием  и высотой, равной значению функции
и высотой, равной значению функции  в точке
в точке  .
.
Геометрически теорема о среднем означает, что на отрезке найдется такая точка, что площадь под кривой  на этом отрезке будет равна площади прямоугольника со сторонами
на этом отрезке будет равна площади прямоугольника со сторонами  и
и  .
.
3. Формула Ньютона-Лейбница
Формула Ньютона-Лейбница связывает неопределенный и определенный интегралы.
Если функция  непрерывна на
непрерывна на  , а функция
, а функция 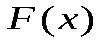 - одна из ее первообразных, т.е.
- одна из ее первообразных, т.е.  , тоопределенный интеграл от функции f(х) на [а, b] равен приращению первообразной F(х) на этом отрезке, то есть
, тоопределенный интеграл от функции f(х) на [а, b] равен приращению первообразной F(х) на этом отрезке, то есть
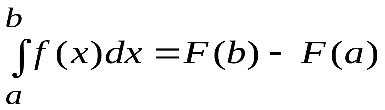 .
.
Эта формула сводит нахождение определенного интеграла к нахождению неопределенного интеграла.
Разность  называется приращением первообразной и обозначается
называется приращением первообразной и обозначается  .
.
Подчеркнем, что при применении формулы Ньютона-Лейбница можно использовать любую первообразную для подынтегральной функции, например, имеющую наиболее простой вид при С = 0 (в дальнейшем не будем записывать константу при нахождении неопределенного интеграла, поскольку будем считать ее равной нулю).
14. Особенности вычисления определенных интегралов.
| При замене переменных (подстановках) | При интегрировании по частям |
| Замена переменных, в отличие от неопределенного интеграла, предполагает не только замену подынтегрального выражения, но и замену пределов интегрирования. | Не следует забывать, что определенный интеграл – это число, при интегрировании по частям пределы интегрирования подставляют во все найденные функции. |
 ;
где новые пределы интегрирования находят как корни уравнений: ;
где новые пределы интегрирования находят как корни уравнений:  ; ;
 . .
| 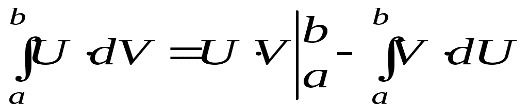
|
15. Применение определенных интегралов для вычисления площадей плоских фигур.
Как следует из геометрического смысла определенного интеграла, для неотрицательной подынтегральной функции интеграл есть площадь криволинейной трапеции, ограниченной отрезками прямых  и кривой
и кривой 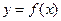 .
.  .
.
В общем случае, когда фигура ограничена сверху кривой 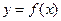 , а снизу -
, а снизу - 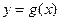 , формула для вычисления площадей принимает вид
, формула для вычисления площадей принимает вид
 . В этой формуле знаки функций
. В этой формуле знаки функций  и
и  значения не имеют.
значения не имеют. 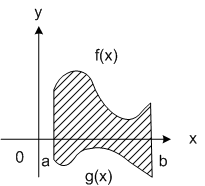
а) Формула площади в декартовых координатах.
Итак, если ограничивающие кривые заданы в декартовых координатах  , то
, то
 .
.
б) Формула площади для кривой, заданной параметрически.
Если  - параметрические уравнения гладкой замкнутой кривой, пробегаемой против часовой стрелки и ограничивающей слева от себя область
- параметрические уравнения гладкой замкнутой кривой, пробегаемой против часовой стрелки и ограничивающей слева от себя область  , то площадь области
, то площадь области 
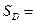
 =
=  , или
, или
 .
.
в) Формула площади в полярной системе координат.
Если  - непрерывная функция при
- непрерывная функция при  , то площадь области
, то площадь области
 вычисляется по формуле
вычисляется по формуле
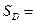
 .
.
ЛИТЕРАТУРА
Основная
1. Письменный Д.Т. Конспект лекций по высшей математике: Полный курс. – М.: Айрис-
пресс, 2004.
2. Высшая математика для экономистов: Учебник. /Под ред. Проф. Н.Ш. Кремера. – М.:
ЮНИТИ-ДАНА, 2007.
3. Высшая математика для экономистов: Практикум. /Под ред. Проф. Н.Ш. Кремера. –
М.: ЮНИТИ-ДАНА, 2007.
Дополнительная
1. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и
задачах. В 2-х частях. – М.: Высшая школа, 2005.
2. Шипачев В. Е. Основы высшей математики. – М.: Высшая школа, 1998.