Решение задачи Коши
Обсуждение методов решения задачи Коши ради простоты будем проводить на примере одного уравнения первого порядка
(6.6)
Построение численных алгоритмов решения уравнения (6.6) опирается на дискретизацию задачи. Введем в области расчета 
дискретный набор точек 
, 
, 
, в которых будет вычисляться приближенное решение (рис. 6.1). Точки 
будем называть узлами интегрирования или узлами сетки, расстояние h между узлами – шагом интегрирования или шагом сетки. Совокупность всех узлов 
будем называть сеточной областью или просто сеткой узлов.
Мы также будем пользоваться другими обозначениями:
– совокупность искомых приближенных значений решения задачи (6.6) в узлах сетки;
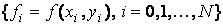– совокупность значений правой части уравнения (6.6) в узлах.
Различные совокупности величин, отнесенных к узлам сетки, называются сеточными функциями [1].
|
Для характеристики точности численных методов определим погрешность приближенного решения следующим образом:
,
где 
– значение точного решения в узле сетки.
Определения. Будем говорить, что численное решение сходится к точному, если 
. Будем также говорить, что метод, по которому получено численное решение, является методом p -го порядка точности, если выполняется неравенство 
.
Переходим к обсуждению конкретных методов получения приближенного решения задачи (6.6) в узлах сетки. Простейший способ их конструирования опирается на замену производной в левой части уравнения (6.6) в окрестности каждого узла приближенным разностным отношением по формулам численного дифференцирования (см. гл. 4, §1).
Методы Рунге-Кутта. Рассмотренные выше метод Эйлера и его модификации являются частными случаями однопараметрического семейства схем Рунге-Кутта различного порядка точности. Так, например, модифицированный метод Эйлера (6.10) и метод Эйлера с пересчетом (6.11) представляют собой частный случай схем Рунге-Кутта второго порядка точности, которые определяются следующим разностным соотношением:
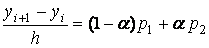, (6.13)
где a – свободный параметр, а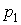 
и 
– вспомогательные величины, вычисляемые по формулам
, 
. (6.13’).
Нетрудно видеть, что при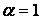 
формулы (6.13) и (6.13’) переходят в формулы модифицированного метода Эйлера (6.10), а при 
в формулы метода Эйлера с пересчетом (6.11).
Широкое распространение на практике получил метод Рунге-Кутта четвертого порядка точности. Расчетные формулы этого метода имеют следующий вид:
(6.14)
где 
– вспомогательные величины.
Метод Рунге-Кутта (6.14) требует существенно большего объема вычислений по сравнению с методом Эйлера и его модификациями, однако это окупается повышенной точностью, что дает возможность проводить вычисления с бóльшим шагом. Другими словами, для получения результатов с одинаковой точностью в методе Эйлера потребуется значительно меньший шаг, чем в методе Рунге-Кутта (6.14).
Выбор шага интегрирования и контроль за точностью вычислений. До сих пор мы не обсуждали вопрос выбора шага интегрирования, а ведь именно от величины шага зависит точность получаемого решения и время, затрачиваемое на его получение. Из приведенных ранее рассуждений о порядке точности методов решения ОДУ можно сделать общий вывод о том, что для повышения точности следует брать меньший шаг. Однако на практике ситуация не столь однозначна. Уменьшение шага интегрирования приводит к увеличению времени вычислений. И что более важно, слишком малые значения шага могут привести не к повышению точности, а, наоборот, к увеличению погрешности в силу накапливания вычислительной ошибки. В тоже время, выбор слишком большого шага интегрирования может привести не только к большой погрешности, но и к получению абсолютно неверного результата. Поэтому выбор шага это всегда определенный компромисс между точностью и временем.
Таким образом, мы обозначили проблему выбора такого значения шага интегрирования, при котором бы обеспечивалась требуемая точность вычисления и умеренные затраты машинного времени. И здесь, прежде всего, нужно определить критерий, по которому можно судить о точности получаемых результатов. В рассмотренном выше численном примере таким критерием являлось сравнение приближенного результата с точным. Однако, если точный результат неизвестен, что и бывает в подавляющем большинстве случаев, то применение такого критерия оказывается невозможным.
Одним из возможных критериев точности может служить сравнение приближенных результатов в каждом узле, полученных при разных шагах интегрирования, например 
и 
. Если величина
сравнима с заданной погрешностью вычислений, то шаг можно увеличить; в противном случае, когда указанная величина слишком велика, значение шага следует уменьшить. Используя эту оценку, можно построить методы с автоматическим выбором шага и контролем точности на протяжении всего времени вычислений. Такие алгоритмы называют адаптивными, т.е. подстраивающимися под условия конкретной задачи.
Другой подход опирается на использование особенностей решаемой задачи. В частности, при решении многих физических задач может существовать такой параметр, например, полная энергия, который должен сохранять свое значение. В ходе вычислений, постоянно отслеживают значение этого параметра и, в случае его изменения, выходящего за пределы допустимой погрешности, корректируют значение шага интегрирования.
Что касается выбора начального (пробного) значения шага, то здесь, к сожалению, не существует универсального рецепта. И в каждом конкретном случае шаг выбирается исходя из характерных параметров решаемой задачи.
21 Численное решение дифференциальных уравнений. Краевые задачи для дифференциальных уравнений. Метод прогонки.
Решение краевой задачи
В предыдущем параграфе рассматривалось решение задачи с начальными условиями, т.е. с условиями в одной (начальной) точке. На практике часто приходится решать задачи другого типа, когда требуется, чтобы искомая функция имела бы заданные значения на границах отрезка, на котором рассматривается решение. Такие задачи, называемые краевыми, получаются при решении уравнений высших порядков или систем уравнений.
Рассмотрим, например, линейное дифференциальное уравнение второго порядка
. (6.18)
Краевая задача состоит в отыскании решения 
уравнения (6.18) на отрезке 
, удовлетворяющего на концах отрезка условиям
, 
. (6.19)
Методы решения краевых задач довольно разнообразные – это и точные аналитические методы, и приближенные, и численные.
Аналитические методы имеются лишь для решения узкого класса уравнений, в частности для решения линейных дифференциальных уравнений с постоянными коэффициентами, которые широко используются при исследовании различных физических процессов (например, в теории колебаний, динамике твердого тела и т.п.).
Приближенные методы разрабатывались еще задолго до появления компьютеров. Однако многие из них до сих пор не утратили своего значения. Это методы коллокаций, наименьших квадратов, метод Галеркина и др.
Численные методы решения краевой задачи можно разделить на две группы: сведение (редукция) решения краевой задачи к последовательности решений задач Коши и непосредственное применение конечно-разностных методов.
Под вопросом(Метод стрельбы (“пристрелки”). Рассмотрим краевую задачу для уравнения второго порядка, разрешенного относительно второй производной:
(6.20)
Заметим, что решение обсуждаемой задачи имеет простой геометрический смысл. Нужно найти интегральную кривую (“траекторию”), проходящую через точки А, В (рис. 6.4). Если в (6.20) заменить условие на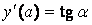 
, то мы получим задачу Коши (задачу с начальными условиями, заданными в точке 
). Считая решение задачи Коши 
, зависящим от параметра a , будем искать такое его значение 
, при котором полученная интегральная кривая 
выходит из точки А и попадает в точку В. Другими словами, нужно подобрать такое значение угла наклона a , чтобы удовлетворялось уравнение
. (6.21)
Следовательно, для нахождения параметра a необходимо решить нелинейное уравнение вида 
, где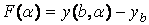 
.
Необычность ситуации состоит в том, что функция 
задана непривычным пока для нас образом – алгоритмически: чтобы найти значение функции F при заданном значении аргумента, надо решить задачу Коши
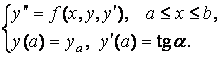(6.22)
Но с точки зрения численных методов решения нелинейных уравнений (см. главу 2) не важно как задана функция, достаточно уметь вычислять её значения. Если, например, из каких-то соображений (или в результате предварительных расчетов) известно, что искомое решение лежит между двумя интегральными кривыми 
и 
с начальными наклонами 
и 
, то простейшим методом решения уравнения (6.21) является метод половинного деления. Полагая 
, решаем задачу Коши при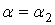 
и, в соответствии с методом половинного деления, отбрасываем один из отрезков: 
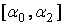или 
, на котором функция не меняет знак. Процесс поиска решения прекращается, если разность двух последовательно найденных значений a меньше некоторого наперед заданного малого числа. В этом случае полученное последним решение задачи Коши и будет принято за искомое решение краевой задачи.
Для решения уравнения (6.21) можно использовать и другие методы, например метод Ньютона. Его применение состоит в следующем. Пусть – начальное приближение к , тогда для уточнения корня можно построить итерационный процесс в соответствии с формулой Ньютона (2.15):
, 
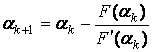(6.23)
Производную 
в знаменателе этого выражения можно вычислить численно:
, (6.24)
где 
– произвольная малая величина.
С учетом (6.24) имеем
, (6.25)
Очевидно, что при использовании метода Ньютона уточнения корня уравнения (6.21) для перехода от k -го приближения к 
-му необходимо два раза решить задачу Коши (6.22): один раз с 
и другой – с 
.
Описанный алгоритм называется методом стрельбы вполне оправдано, поскольку в нем как бы проводится “пристрелка” по углу наклона интегральной кривой (“траектории”) в начальной точке. Следует отметить, что этот алгоритм хорошо работает в том случае, если решение не слишком чувствительно к изменению a ; иначе мы можем столкнуться с неустойчивостью решения. В тех случаях, когда решения дифференциальных уравнений являются быстро растущими функциями, предпочтительней могут оказаться методы, основанные на непосредственной аппроксимации исходной задачи (см., например, [12]).
Метод мат прогонки
Пусть на отрезке 
задано линейное обыкновенное дифференциальное уравнение
(1)
где квадратная матрица (х).порядка n и вектор f(x) 
- известные непрерывные функции, дифференцируемая вектор-функция у(х) = 
подлежит определению. К уравнению (1) присоединены граничные условия в форме
(2)
где известные матрицы j и y имеют размеры nx kи n x l и ранги k и l соответственно,
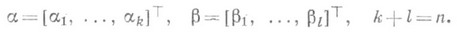
Используя дифференциальные уравнения
с начальными условиями u(а)=j, g(а)=a, где искомая дифференцируемая матрица-функция и(х).имеет размеры 
, можно определить и(х).и g(х).на всем отрезке 
(прямой ход прогонки). С помощью уравнения
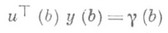
и второго из граничных условий (2) можно определить значение у(b), если квадратная матрица [и(b), y] имеет ранг п. Искомое решение граничной задачи (1)-(2) вычисляется теперь как решение задачи Коши для уравнения (1) в направлении от точки х=b к точке х=а (обратный ход прогонки). Указанный метод применим и к многоточечной задаче, когда условия вида (2) задаются не только на концах, но и в нескольких внутренних точках отрезка 
Разработаны варианты метода прогонки для переноса линейных граничных условий, отличных от (2) (см. [1]).
Достоинства П. м. видны на примере следующей граничной задачи:
где квадратная матрица Q(x).порядка пи вектор f(х).размера п - известные непрерывные функции, дважды дифференцируемая вектор-функция у(х).подлежит определению, известные квадратные матрицы j и y имеют
порядок 
Используя дифференциальные уравнения
с начальными условиями v(а)=j, g(a)=a, где искомая дифференцируемая квадратная матрица-функция v(х).имеет порядок 
, ищутся v(x).и g(х).на всем отрезке 
(прямой ход прогонки).
С помощью уравнения
и граничного условия (5) можно определить значение
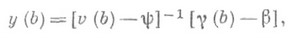(6)
если матрица v(b) - y имеет ранг п. Искомое решение граничной задачи (3) - (5) находится как решение задачи Коши для уравнения
с начальным условием (6) (обратный ход прогонки). Таким образом, П. м. для задачи (3) - (5) является методом понижения порядка дифференциального уравнения (3).
В случае конечной последовательности линейных алгебраич. уравнений
(7)
где коэффициенты а i, с i, bi - - известные квадратные матрицы порядка v, a fi и j i - известный и искомый вектор-столбцы размера v, a1 =0, с n =0, алгоритм прогонки определяется следующим образом:
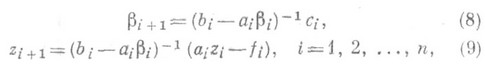
при условиях b 1 =0, z1=0 (прямой ход) и
при условии j n+1 =0 (обратный ход). Здесь b i - квадратная матрица порядка v, zi и j i - вектор-столбцы размера v. Изложенный метод наз. методом правой прогонки. Аналогично формулам (8)- (10) получаются формулы левой прогонки. Комбинируя левую и правую прогонки, получают метод встречных прогонок. При решении уравнений (7) с сильно меняющимися коэффициентами применяется потоковый метод прогонки. Для нахождения периодич. решения бесконечной последовательности уравнений вида (7) с периодич. коэффициентами используется циклическая прогонка (см. [4]).,
22 Численное решение дифференциальных уравнений. Уравнения с частными производными. Элементы теории разностных схем.
Одномерное уравнение теплопроводности
Уравнение, описывающее распространение тепла в однородном стержне имеет вид
где u (t, x) — температура, и α — положительная константа, описывающая скорость распространения тепла. Задача Коши ставится следующим образом:
,
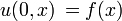где f (x) — произвольная функция.