· Задачи теории вероятностей.
Теория вероятностей – это математическая наука, изучающая закономерности случайных явлений, т.е. таких явлений, которые при неоднократном повторении каждый раз протекают по-разному.
Комбинаторика – это раздел теории вероятностей, в котором решаются задачи на составление различных комбинаций из конечного числа элементов, удовлетворяющих некоторым условиям и подсчета числа всех возможных комбинаций.
· Элементы комбинаторики. Перестановки, размещения, сочетания
Существует три типа комбинаторных задач: 1) на составление перестановок, 2) на составление размещений, 3) на составление сочетаний
Перестановки - всевозможные упорядоченные комбинации, состоящие из n различных элементов. Число перестановок вычисляется по формуле: 
Размещения - всевозможные упорядоченные комбинации m элементов, составленные из n различных элементов, вычисляется по формуле: 
Сочетания - всевозможные неупорядоченные комбинации m элементов, составленные из n различных элементов, вычисляется по формуле: 
· Понятие испытания и события. Виды событий. Сумма и произведение событий
Событие – это факт, который при осуществлении определенных условий может произойти или нет. События обозначаются большими буквами латинского алфавита А, В,С...
Виды событий:
Достоверное событие – это событие, которое в результате испытания непременно должно
произойти.
Невозможное событие – это событие, которое в результате испытания не может произойти.
Случайное событие – это событие, которое при испытаниях может произойти или не может
произойти.
Несовместные события - события, если в результате данного испытания появление одного
из них исключает появление другого.
Совместные события - события, если в результате данного испытания появление одного из
них не исключает появление другого.
Равновозможные события - события, если нет оснований считать, что одно из них
происходит чаще, чем другое.
События образуют полную группу событий, если в результате испытания обязательно
произойдет хотя бы одно из них и любые два из них несовместны.
Противоположные события - два несовместных события А и Ā (читается «не А »), если в
результате испытания одно из них должно обязательно произойти.
Операции над событиями
Суммой нескольких событий называется событие, состоящее в наступлении хотя бы одного из них в результате испытания.
Произведением нескольких событий называется событие, которое состоит в совместном наступлении всех этих событий в результате испытания.
· Определение вероятности события
Вероятность события – это число, характеризующее степень возможности появления событий при многократном повторении событий.
Вероятность обозначается буквой Р (probability (англ.) – вероятность).
Классическое определение вероятности: Вероятностью Р(А) события А называется
отношение числа благоприятствующих исходов m к общему числу равновозможных
несовместных исходов n: Р(А)= m/n
Свойства вероятности:
Вероятность случайного события А находится между 0 и 1, т.е. 0<Р(А)<1
Вероятность достоверного события равна 1
Вероятность невозможного события равна 0
Условная вероятность – вероятность наступления событий, вычисленная в предположении, что событие уже произошло.
· Теоремы сложения и умножения вероятностей. Формула полной вероятности
Теоремы сложения вероятностей
Вероятность суммы двух несовместных событий А и В равна сумме вероятностей этих
событий: Р(А+В)=Р(А)+Р(В).
Вероятность появления хотя бы одного из двух совместных событий равна сумме
вероятностей этих событий без вероятности их совместного наступления:
Р(А+В)=Р(А)+Р(В)-Р(А*В).
Теоремы умножения вероятностей
Вероятность произведения 2 независимых событий А и В равна произведению вероятностей
этих событий: Р(А*В)=Р(А)*Р(В)
Вероятность совместного появления двух зависимых событий равна произведению одного
из них на условную вероятность второго при условии первого:
P(AB)=P(A)*P(B/A)=P(B)*P(A/B)
Формула полной вероятности
Пусть событие А может быть реализовано только при условии появления одного из событий Hi, i = 1,..., n. Предположим, что события Hi несовместны, образуют полную группу (т.е. в результате испытания непременно произойдет одно из них) и вероятности их до опыта известны. Такие события Hi называются гипотезами.Тогда вероятность события А можно вычислить с помощью формулы полной вероятности: 
· Случайная величина. Способы задания случайной величины. Определения непрерывной и дискретной случайных величин
Случайная величина - величина, которая принимает в результате испытания то или иное возможное значение, заранее неизвестное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств.
Случайные величины могут быть дискретными и непрерывными.
Дискретной называют такую случайную величину, которая принимает счётное
множество значений
Непрерывной называют такую случайную величину, которая может принимать любые значения в определённом интервале. Занумеровать все значения величины, попадающие даже в узкий интервал принципиально невозможно.
Случайные величины обозначают прописными буквами латинского алфавита X, Y, Z, а их возможное значение – соответствующими строчными буквами x, y, z.
При многократных испытаниях определённые значения случайной величины могут встречаться несколько раз. Поэтому, для задания случайной величины недостаточно перечислить лишь все
её возможные значения. Необходимо также знать, как часто могут появляться те или иные значения в результате испытания при одних и тех же условиях, т.е. нужно задать вероятности их появления.
Случайная величина считается заданной, если известен закон распределения случайной величины.
Распределением (законом распределения) случайной величины называется всякое соотношение между возможными значениями случайной величины и соответствующими им вероятностями.
Распределение дискретной случайной величины может быть задано в виде таблицы, в графическом и аналитическом виде.
Пусть дискретная величина X принимает значения Х=х1, Х=х2,…, Х=хn. Обозначим вероятности этих событий соответственно: Р(Х = х1) = р1, Р(Х = х2) = р2,…, Р(Х = хn) = рn.
Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания распределения дискретной случайной величины:
| Значение случайной величины х1 | х1 | х2 | … | хn |
| Вероятности значений р1 | р1 | р2 | … | рn |
Так как в результате испытания случайная величина Х всегда примет одно из своих возможных значений х1, х2, … хn, то эти случайные события образуют полную группу событий и
n
р1 + р2 + …+ рn = ∑ pi = 1.
i =1
Табличную формулу задания называют также рядом распределения.
Для наглядности ряд распределения можно представить в графическом виде, где по оси абсцисс откладываются значения случайной величины, а по оси ординат вероятности этих значений
· Закон распределения случайной величины
Законом распределения случайной величины называется соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями (его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая - их вероятности (Табл.1).
Таблица 1
| Х | х1 | х2 | ... | хn |
| p | p1 | p2 | ... | pn |
Сумма вероятностей второй строки таблицы 1, равна единице:
p1 + p2 +...+ pn = 1.
· Числовые характеристики дискретной случайной величины: математическое ожидание, дисперсия, среднее квадратическое отклонение
Закон распределения полностью характеризует случайную величину. Но при решении ряда практических задач нет необходимости знать все возможные значения случайной величины и соответствующие им вероятности, а удобнее пользоваться некоторыми количественными показателями, которые в сжатой форме дают достаточную информацию о случайной величине. Такие показатели называются числовыми характеристиками случайной величины. Основными из них являются: математические ожидание, дисперсия и среднее квадратическое отклонение.
Математическое ожидание характеризует положение случайной величины на числовой оси, определяя некоторое среднее значение, около которого сосредоточены все возможные значения случайной величины.
Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных её значений на соответствующие вероятности: 
Дисперсия характеризует рассеяние (отклонение) случайной величины относительно математического ожидания. Дисперсия случайной величины Х - математическое ожидание квадрата отклонения случайной величины Х от её математического ожидания М (Х), обозначают D(X), т.е. D(X) = M(X – M(X))2
Для дискретных случайных величин эту формулу можно записать в следующем виде: 
Для вычислений удобно использовать формулу: D(Х) = М(Х2) –М2(Х)
Размерность дисперсии равна квадрату случайной величины и её неудобно использовать для характеристики разброса, поэтому удобнее применять корень квадратный из дисперсии – среднее квадратическое отклонение. Эта величина даёт представлять о размахе колебаний случайной величины около математического ожидания: 
(Х) = 
· Функция распределения случайной величины и её график
Функция распределения
В ряде практических случаев вместо вероятности того, что случайная величина Х принимает некоторое определённое значение хi,необходимо знать, что случайная величина Х меньше хi. Эта вероятность задаётся интегральной функцией распределения.
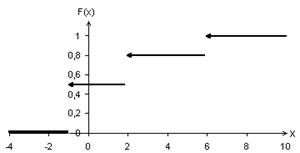
Функция распределения определяет вероятность того, что случайная величина Х принимает значение, меньшее фиксированного действительного числа х, т.е. F(x) = P(X<x).
Функцию распределения F(x) иногда называют интегральной функцией распределения или интегральным законом распределения.
Функцию F(x) можно получить, суммируя значения вероятностей по тем значениям случайной величины, которые меньше xi, т. е. F(xi) = P (X<xi) = ∑ P(xi), где неравенство x<xi под знаком суммы показывает, что суммирование распространяется на все значения х меньше xi.
Для дискретной случайной величины график функции распределения представляет собой разрывную ступенчатую функцию. Когда переменная х принимает какое-нибудь из своих возможных значений, функция распределения увеличивается скачкообразно на величину вероятности этого значения. Причём при переходе слева к точкам разрыва функция сохраняет своё значение. На графике это отмечено чёрной точкой. Сумма величин всех скачков функции F(x) равна 1.
· Предмет математической статистики, основные задачи статистики. Область применения статистических методов
Математическая статистика — раздел прикладной математики, наука о математических методах систематизации и использования статистических данных для научных и практических выводов. Во многих своих разделах математическая статистика опирается на теорию вероятности, позволяющую оценить надежность и точность выводов. Этот раздел прикладной математики посвящен изучению случайных величин по результатам наблюдений.
В прикладных задачах вероятность исследуемого события обычно неизвестна. Она
определяется приближенно по статистическим данным. Дать оценку полученной на основе опытных данных, вероятности события - одна из основных задач математической статистики.
Разработать методы анализа статистических данных зависимости от целей исследования. определить ее распределение с точностью до некоторого неизвестного параметра. Дать оценку этого параметра в виде числа или интервала, в котором с заданной вероятностью заключено значение неизвестного параметра.
Методы математической статистики широко применяются в самых различных областях знаний - в физике, звездной астрономии, экономике, геологии, гидрологии, климатологии, биологии, медицине и др. Также широко используется математическая статистика и в промышленности. Исходным материалом являются статистические данные.
· Понятие о генеральной совокупности и выборке
Генеральная совокупность - совокупность всех исследуемых объектов.
· Статистическое распределение. Гистограмма. Полигон
Статистическое распределение – это таблица, в первой строке которой записаны все различные значения выборки в порядке возрастания, а во второй строке указаны соответствующие им частоты
Выборочной средней (выборочным математическим ожиданием ) 
называют среднее
арифметическое значение признака выборочной совокупности.
Если все значения 
признака выборки объема 
различны, то: 
Если же значения признака 
имеют соответственно частоты 
, причем 
, то 
или 
.
Выборочной дисперсией 
называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения .
Если все значения признака выборки объема различны, то 
Если же значения признака имеют соответственно частоты , причем , то
Выборочное среднее квадратическое отклонение – это квадратный корень из
выборочной дисперсии.
· Характеристики положения и рассеяния статистического распределения
Статистическое распределение содержит полную информацию об изменчивости (вариации) признака. Однако на практике часто нет необходимости непосредственно использовать статистическое распределение, достаточно знать некоторые сводные характеристики, которые довольно успешно и полно описывают основные свойства распределения.
Для описания основных свойств статистических распределений чаще всего используют выборочные характеристики следующих видов: 1) средние; 2) характеристики вариации (рассеяния).
Существуют различные виды средних: средняя арифметическая, средняя геометрическая, средняя гармоническая и др. Это так называемые аналитические средние. Основным видом аналитических средних является средняя арифметическая, или выборочная средняя. Выборочная средняя 
характеризует типичное для выборки значение признака Х. Она также приближенно характеризует (оценивает) типичное для генеральной совокупности значение признака Х.
Если данные наблюдения не сгруппированы, то выборочная средняя рассчитывается как простая средняя арифметическая:
.
Если же данные сгруппированы, то выборочная средняя рассчитывается как взвешенная средняя по одной из следующих формул:
Здесь частоты mi и частости wi являются весами.
Следует отметить, что данные формулы непосредственно применимы только к статистическому распределению дискретного признака (дискретному ряду).
Кроме рассмотренной средней арифметической, для статистических распределений используют еще структурные, или порядковые, средние. Из них наиболее часто применяют медиану и моду.
Медианах ме- это серединное значение признака Х, то есть значение признака, которое делит ранжированный вариационный ряд на две равные по численности группы. Медиана х меопределяется следующим образом:
, если n = 2 j - четное;
х ме = хj+ 1, если n = 2 j +1 - нечетное.
Из определения накопленной относительной частоты следует, что
.
· Статистические оценки параметров распределения
Величину 
называют точностью оценки. Чем меньше, тем лучше, точнее определён неизвестный параметр.
К оценке любого параметра предъявляется ряд требований, которым она должна удовлетворять, чтобы быть «близкой» к истинному значению параметра, т.е. быть в каком-то смысле «доброкачественной» оценкой. Качество оценки определяют, проверяя, обладает ли она свойствами несмещённости, эффективности и состоятельности.
Оценка параметра θ называется несмещённой (без систематических ошибок), если математическое ожидание оценки совпадает с истинным значением θ:
. (1)
Если равенство (1) не имеет места, то оценка называется смещённой (с систематическими ошибками). Это смещение может быть связано с ошибками измерения, счёта или неслучайным характером выборки. Систематические ошибки приводят к завышению или занижению оценки.
Для некоторых задач математической статистики может существовать несколько несмещённых оценок. Обычно предпочтение отдают той, которая обладает наименьшим рассеянием (дисперсией).
Оценка называется эффективной, если она имеет наименьшую дисперсию среди всех возможных несмещённых оценок параметра θ.
Пусть D () – минимальная дисперсия, а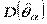 
– дисперсия любой другой несмещённой оценки 
параметра θ. Тогда эффективность оценки равна
. (2)
Ясно, что 
. Чем ближе 
к 1, тем эффективнее оценка. Если 
при 
, то оценка называется асимптотически эффективной.
Замечание: Если оценка смещённая, то малости её дисперсии ещё не говорит о малости её погрешности. Взяв, например, в качестве оценки параметра θ некоторое число 
, получим оценку даже с нулевой дисперсией. Однако в этом случае ошибка (погрешность) 
может быть сколь угодно большой.
Оценка называется состоятельной, если с увеличением объема выборки () оценка сходится по вероятности к точному значению параметра θ, т.е. если для любого 
. (3)
Состоятельность оценки параметра θ означает, что с ростом n объема выборки качество оценки улучшается.
Теорема 1. Выборочная средняя является несмещённой и состоятельной оценкой математического ожидания.
Теорема 2. Исправленная выборочная дисперсия является несмещённой и состоятельной оценкой дисперсии.
Теорема 3. Эмпирическая функция распределения выборки является несмещённой и состоятельной оценкой функции распределения случайной величины.