Кроме того, аномальные уровни во временных рядах могут возникать из-за воздействия факторов, имеющих объективный характер, но проявляющихся эпизодически или очень редко – ошибки второго рода, они устранению не подлежат.
Для выявления аномальных уровней временных рядов используются методы, рассчитанные для статистических совокупностей.
Метод Ирвина.
Метод Ирвина предполагает использование следующей формулы:
, (1)
где среднее квадратическое отклонение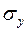 
рассчитывается в свою очередь с использованием формул:
. (2)
Расчетные значения 
сравниваются с табличными значениями критерия Ирвина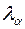 
, и если оказываются больше табличных, то соответствующее значение 
уровня ряда считается аномальным. Значение критерия Ирвина для уровня значимости 
, т.е. с 5%-ной ошибкой, приведены в таблице 4.
Таблица 4.
| |||||||
|
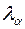
| 2,8 | 2,3 | 1,5 | 1,3 | 1,2 | 1,1 | 1,0 |
После выявления аномальных уровней ряда обязательно определение причин их возникновения!
Если точно установлено, что аномалия вызвана ошибками первого рода, то соответствующие уровни ряда «поправляются» либо заменой простой средней арифметической соседних уровней ряда, либо значениями, полученными по кривой, аппроксимирующей данный временной ряд в целом.
Метод проверки разностей средних уровней.
Реализация этого метода состоит из четырех этапов.
1. Исходный временной ряд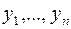 
разбивается на две примерно равные по числу уровней части: в первой части 
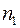первых уровней исходного ряда, во второй – 
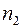остальных уровней 
.
2. для каждой из этих частей вычисляются среднее значение и дисперсии:
3. проверка равенства (однородности) дисперсий обеих частей ряда с помощью F-критерия Фишера, которая основана на сравнении расчетного значения этого критерия:
с табличным (критическим) значением критерия Фишера 
с заданным уровнем значимости (уровнем ошибки) 
. В качестве чаще всего берут значения 0,1 (10%-ная ошибка), 0,05 (5%-ная ошибка), 0,01 (1%-ная ошибка). Величина 
называется доверительной вероятностью. Если расчетное (эмпирическое) значение F меньше табличного , то гипотеза о равенстве дисперсий принимается и переходят к четвертому этапу. В противном случае, гипотеза о равенстве дисперсий отвергается и делается вывод, что данный метод для определения наличия тренда ответа не дает.
4. проверяется гипотеза об отсутствии тренда с использованием 
критерия Стьюдента. Для этого определяется расчетное значение критерия Стьюдента по формуле:
(3)
где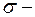 
среднее квадратическое отклонение разности средних:
.
Если расчетное значение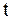 
меньше табличного значения статистики Стьюдента 
с заданным уровнем значимости , гипотеза принимается, то есть тренда нет, в противном случае тренд есть. Заметим, что в данном случае табличное значение берется для числа степеней свободы, равного 
, при этом данный метод применим только для рядов с монотонной тенденцией.
Метод Фостера-Стьюарта.
Этот метод обладает большими возможностями и дает более надежные результаты по сравнению с предыдущими. Кроме тренда самого ряда (тренда в среднем), он позволяет установить наличие тренда дисперсии временного ряда: если тренда дисперсии нет, то разброс уровней ряда постоянен; если дисперсия увеличивается, то ряд «раскачивается» и т.д.
Реализация метода также состоит из четырех этапов.
1. производится сравнение каждого уровня со всеми предыдущими, при этом определяются две числовые последовательности:
2. вычисляются величины:
Нетрудно видеть, что величина 
, характеризующая изменение временного ряда, принимает значения от 0 (все уровни ряда равны между собой) до 
(ряд монотонный). Величина 
характеризует изменение дисперсии уровней временного ряда и изменяется от 
(ряд монотонно убывает) до 
(ряд монотонно возрастает).
3. проверка гипотез: можно ли считать случайными
1. отклонение величины от величины 
математического ожидания величины для ряда, в котором уровни расположены случайным образом;
2. отклонение величины от нуля.
Эта проверка проводится с использованием расчетных (эмпирических) значений критерия Стьюдента для средней и для дисперсии:
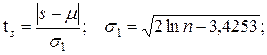
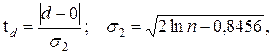
где математическое ожидание величины , определенной для ряда, в котором уровни расположены случайным образом;
среднее квадратическое отклонение для величины ;
среднее квадратическое отклонение для величины .
Имеются табличные значения величин 
, 
и 
; фрагмент этих значений представлен в таблице 5.
Таблица 5.
|
| ||||
|
| 3,858 | 5,195 | 5,990 | 6,557 |
|
| 1,288 | 1,677 | 1,882 | 2,019 |
|
| 1,964 | 2,279 | 2,447 | 2,561 |
4. эмпирические значения 
и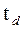 
сравниваются с табличными значениями критерия Стьюдента с заданным уровнем значимости . Если эмпирическое значение меньше табличного, то гипотеза об отсутствии соответствующего тренда принимается; в противном случае тренд есть.