Постановка задачи
Используя теорему Куна-Таккера и встроенные функции минимизации математического пакета WolframMathematica, найти минимум функции

При следующих ограничениях:


Полученные результаты представить в виде отчета, включающего в себя:
1.Иcследование выпуклости целевой функции и функций-ограничений;
2.Исследование регулярности области;
3.Пошаговое решение с использованием теоремы Куна-Таккера;
4.Исследование найденных решений;
5.Сравнение с решением, найденным при помощи встроенных функций.
Исследование выпуклости целевой функции и функций-ограничений
Рассмотрим множество ограничений:


Ограничения не аффины, следовательно, проверим их на выпуклость:






Рассматривая  имеем собственные числа разных знаков (
имеем собственные числа разных знаков ( ), Гессиан не является неотрицательно-определенным, значит множество ограничений невыпукло.
), Гессиан не является неотрицательно-определенным, значит множество ограничений невыпукло.
Поскольку множество ограничений не выпукло, то рассматривать целевую функцию на этом множестве не имеет смысла, так как на невыпуклом множестве целевую функцию невсегда можно проверить на выпуклость.

Иcследование регулярности области
Мы не будем рассматривать регулярность области, поскольку область невыпукла.
Пошаговое решение с использованием теоремы Каруша- Куна- Таккера
Рассмотрим задачу о нахождении допустимых значений x, при которых
функция Q(x)достигает минимума в области  .
.
Запишем задачу в виде:  предполагая, что минимум существует.
предполагая, что минимум существует.

Теорема Каруша-Куна-Такера будет носить необходимый характер, поэтому нам надо перебрать все возможные комбинации активных ограничений, чтобы найти минимум функции.

Решать получившиеся системы будем численно в пакете Матлаб при помощи функции vpasolve();
1. Пусть  =1.
=1.
2. Выберем активные ограничения:
1. I = {  }
}
Получим систему


Решение x1=-1.15, y1 = -2.08, x2= 0.446, y2= 0.358.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
2. I = {  }
}

Решение x= 2.46, y = 1.04,  = 0.3499.
= 0.3499.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
3. I = {  }
}

Решение x1 = 1.615, y1 = 0.445,  = -7.26;x2= -0.11479, y2 = -0.0717,
= -7.26;x2= -0.11479, y2 = -0.0717,  = -0.181.
= -0.181.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
4. I = {  }
}

Решение x= 0.147, y = 0.6419,  = 0.276.
= 0.276.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
5. I = {  }
}

Решение x= 0.211, y = 0.176,  = -0.1924,
= -0.1924,  = -1.0604.
= -1.0604.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
6. I = {  }
}

Решение x= 0.0980, y = 0.2,  = 0.08,
= 0.08,  = -0.34.
= -0.34.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
7. I = {  }
}

Решение x= 1.776, y = 0.25,  = 0.497,
= 0.497,  = -0.795.
= -0.795.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
3. Пусть  =0
=0
4. Выберем активные ограничения:
1. I = {  }
}

Решение x= 0, y = 1,  = 0.
= 0.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
2. I = {  }
}

Решение x= 0, y = 8.24,  = 0.
= 0.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
3. I = {  }
}

Решение x= 0, y = 0,  = 0.34.
= 0.34.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
4. I = {  }
}

Решение x= 0, y = 0,  = -0.192,
= -0.192,  = 0.59.
= 0.59.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
5. I = {  }
}
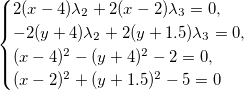
Решение x= 0, y = 0,  = 0.08,
= 0.08,  = -0.34.
= -0.34.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
6. I = {  }
}

Решение x= 0, y = 0,  = 0.497,
= 0.497,  = -0.795.
= -0.795.
Ни один из наборов не удовлетворяет ограничениям g1,g2,g3;
Исследование найденных решений
Исследовать можно было бы, но делать ввиду их отсутствия я этого не буду
Сравнение с решением, найденным при помощи встроенных функций
1.Минимизация функции без ограничений проводилась при помощи функцииfminsearch.
За 62 итерации было достигнуто минимальное значение функции 0,17545, в точке x = -1.158, y = -2.081
2.Минимизация функции с ограничениямипроводилась при помощи функцииfmincon.
За 33 итерации было достигнуто минимальное значение функции 0,763, в точке x = 1.0428, y = 0.3499.

Вывод
В данной лабораторной работе был найден минимум функции

При следующих ограничениях:


Глобальным минимумом является точка (1.04, 0.34). Значение функции в этой точке 0.763. Анализ полученных результатов показал, что решение данной задачи, может проводиться разными способами. Как при помощи Matlab, так и в ручную. Решения получаются одинаковыми.
Solvers.m
clear;
symsx;
symsy;
symsl1;
symsl2;
symsl3;
g1 = 1+y^3-x == 0;
g2 = (x-4)^2-(y+4)^2-2==0;
g3 = (x-2)^2+(y+1.5)^2-5==0;
Qx = 2*y*sin(x*y)*(1-cos(x*y)+y)+3*(sin(x+y+2)+x^2)^2*(2*x+cos(x+y+2));
Qy = 2*(x*sin(x*y)+1)*(1-cos(x*y)+y)+3*(sin(x+y+2)+x^2)^2*cos(x+y+2);
l1x = -l1;
l2x = 2*(x-4)*l2;
l3x = 2*(x-2)*l3;
l1y = 3*y^2*l1;
l2y = -2*(y+4)*l2;
l3y = 2*(y+1.5)*l3;
[sol_x, sol_y] = vpasolve(Qx, Qy,[0 0],'random',true)
[sol_x, sol_y, sol_l1] = vpasolve(Qx + l1x, Qy +l1y, g1,[-1 2 -1],'random',true)
[sol_x, sol_y, sol_l2] = vpasolve(Qx + l2x, Qy +l2y, g2,'random',true)
[sol_x, sol_y, sol_l3] = vpasolve(Qx + l3x, Qy +l3y, g3,[-1 2 -1],'random',true)
[sol_x, sol_y, sol_l1, sol_l2] = vpasolve(Qx + l1x + l2x, Qy + l1y + l2y, g1, g2,[-1 2 0 0],'random',true)
[sol_x, sol_y, sol_l1, sol_l3] = vpasolve(Qx + l1x + l3x, Qy + l1y + l3y, g1, g3,[-1 2 0 0],'random',true)
[sol_x, sol_y, sol_l2, sol_l3] = vpasolve(Qx + l2x + l3x, Qy + l2y + l3y, g2, g3,'random',true)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
[sol_x, sol_y] = vpasolve(Qx, Qy,'random',true)
[sol_x, sol_y, sol_l1] = vpasolve(l1x, l1y, g1,'random',true)
[sol_x, sol_y, sol_l2] = vpasolve(l2x, l2y, g2,'random',true)
[sol_x, sol_y, sol_l3] = vpasolve(l3x, l3y, g3,'random',true)
[sol_x, sol_y, sol_l1, sol_l2] = vpasolve(l1x + l2x, l1y + l2y, g1, g2,'random',true)
[sol_x, sol_y, sol_l1, sol_l3] = vpasolve(l1x + l3x, l1y + l3y, g1, g3,'random',true)
[sol_x, sol_y, sol_l2, sol_l3] = solve(l2x + l3x, l2y + l3y, g2, g3,'random',true)
(1+sol_y^3-sol_x)<=0
(sol_x-4)^2-(sol_y+4).^2-2<=0
(sol_x-2)^2+(sol_y+1.5)^2-5<=0
Plot.m
clear;
x= [0:0.01:6];
y= [-4:0.01:2];
[X,Y] = meshgrid(x, y);
xlabel('X');
ylabel('Y');
Z = (1-cos(X.*Y)+Y).^2+(sin(X+Y+2)+X.^2).^3;
g1 = 1+Y.^3-X<=0;
g2 = (X-4).^2-(Y+4).^2-2<=0;
g3= (X-2).^2+(Y+1.5).^2-5<=0;
g=g1&g2&g3;
hold on;
colorbar;
colormapredbluecmap;
cgo=contourf(X, Y, Z);
contour(X,Y,g,'w');
plot3(1.0428, 0.3499, 0.763,'o','MarkerEdgeColor','g','MarkerSize',6);
FindLocal.m
clear;
symsx1x2real
x = [x1;x2];
f = (1-cos(x1*x2)+x2).^2+(sin(x1+x2+2)+x1.^2).^3;
gradf = jacobian(f,x).'; % column gradf
hessf = jacobian(gradf,x);
fh = matlabFunction(f,gradf,hessf,'vars',{x});
[X,Y] = meshgrid(-6:.01:6);
g1 = (1+Y.^3-X<=0);
% Z=1 where the first constraint is satisfied, Z=0 otherwise
g2 = ((X-4).^2-(Y+4).^2-2<=0);
% Z=2 where the second is satisfied, Z=3 where both are
g3 = ((X-2).^2+(Y+1.5).^2-5<=0);
Z = g1+g2+g3;
surf(X,Y,Z,'LineStyle','none');
fig = gcf;
fig.Color = 'w'; % white background
view(0,90)
hold on
%plot3(.4396,.0373, 4,'o','MarkerEdgeColor','r','MarkerSize',8);
% best point
xlabel('x')
ylabel('y')
hold off
W = (1-cos(X*Y)+Y).^2+(sin(X+Y+2)+X.^2).^3;
W(Z < 3) = nan;
surf(X,Y,W,'LineStyle','none');
view(68,20)
holdon
%plot3(.4396,.0373,.8152,'o','MarkerEdgeColor','r',...
% 'MarkerSize',8); % best point
xlabel('x')
ylabel('y')
zlabel('z')
hold off
c1 = 1+x2^3-x1;
c2 = (x1-4)^2-(x2+4)^2-2;
c3 = (x1-2)^2+(x2+1.5)^2-5;
c = [c1 c2 c3];
gradc = jacobian(c,x).'; % transpose to put in correct form
constraint = matlabFunction(c,[],gradc,[],'vars',{x});
hessc1 = jacobian(gradc(:,1),x); % constraint = first c column
hessc2 = jacobian(gradc(:,2),x);
hessfh = matlabFunction(hessf,'vars',{x});
hessc1h = matlabFunction(hessc1,'vars',{x});
hessc2h = matlabFunction(hessc2,'vars',{x});
myhess = @(x,lambda)(hessfh(x) +...
lambda.ineqnonlin(1)*hessc1h(x) +...
lambda.ineqnonlin(2)*hessc2h(x));
options = optimoptions('fmincon',...
'Algorithm','interior-point',...
'SpecifyObjectiveGradient',true,...
'SpecifyConstraintGradient',true,...
'HessianFcn',myhess,...
'Display','final');
% fh2 = objective without Hessian
fh2 = matlabFunction(f,gradf,'vars',{x});
[xfinal,fval,exitflag,output] = fmincon(fh2,[-1;2],...
[],[],[],[],[],[],constraint,options)
options = optimoptions('fmincon','Algorithm','interior-point',...
'Display','final');
% fh3 = objective without gradient or Hessian
fh3 = matlabFunction(f,'vars',{x});
% constraint without gradient:
constraint = matlabFunction(c,[],'vars',{x});
[xfinal,fval,exitflag,output2] = fmincon(fh3,[-1;2],...
[],[],[],[],[],[],constraint,options)
sprintf(['There were %d iterations using gradient'...
' and Hessian, but %d without them.'],...
output.iterations,output2.iterations)
sprintf(['There were %d function evaluations using gradient'...
' and Hessian, but %d without them.'],...
output.funcCount,output2.funcCount)
Primfun.m
function f = primfung(x)
f=(1-cos(x(1)*x(2))+x(2))^2+(sin(x(1)+x(2)+2)+x(1)^2)^3;
end
Primcon.m
function [c,ceq] = primcon(x)
%Primer for fmincon
c=[1+x(2)^3-x(1);(x(1)-4)^2-(x(2)+4)^2-2; (x(1)-2)^2+(x(2)+1.5)^2-5];
ceq=[];
end