1.
Смоделируйте выборку значений случайной величины, имеющей экспоненциальное распределение с заданным значением параметра l.
2.
Определите логарифм функции максимального правдоподобия и изобразите его график (в примере рис.3.2 а).
3.
Смоделируйте несколько выборок разного объема значений случайной величины, имеющей экспоненциальное распределение с заданным значением параметра l.
4.
Вычислите оценку максимального правдоподобия от объема выборки.
5.
Изобразите на графике зависимость оценки максимального правдоподобия от объема выборки (в примере рис. 3.2 б).
Пример выполнения задания
В приведенном ниже фрагменте рабочего документа выполнены требуемые вычисления для экспоненциального распределения с параметром l = 2.
а) Логарифм функции максимального правдоподобия
б) Зависимость оценки максимального правдоподобия от объема выборки
Рис. 3.2
Обратимся еще к одному примеру. Рассмотрим распределение, которое зависит более чем от одного параметра.
Пусть случайная величина h имеет распределение Лапласа, зависящее от двух неизвестных параметров 
и 
: 
, и 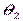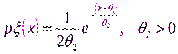пусть 
– выборка из генеральной совокупности, отвечающей случайной величине h. Задача состоит в построении методом максимального правдоподобия оценок 
и 
параметров 
и 
.
Для рассматриваемого нами распределения функция максимального правдоподобия имеет вид
и
.
Здесь нельзя использовать необходимое условие экстремума для гладких функций, так как функция lnL (а значит, и функция L) не дифференцируема по 
. Однако задача легко решается, поскольку при постоянном 
максимум lnL, очевидно, достигается в точке минимума функции 
. Если объем выборки п – нечетное число, то оценка 
совпадает с медианой выборки 
. При четном п минимум 
достигается в любой точке отрезка между проранжированными наблюдениями с номерами 
и 
.
Оценка максимального правдоподобия 
параметра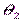 
удовлетворяет уравнению 
и имеет вид 
, т.е. равна средней величине модуля отклонения выборочных значений от 
.
Замечание. В Mathcad нет функции, генерирующей выборки случайных величин, имеющих распределение Лапласа. Однако, поскольку плотность распределения Лапласа всюду непрерывна1, можно моделировать распределенные по Лапласу случайные величины из выборок равномерной величины. Обозначим 
функцию, обратную функции распределения 
. Такая функция определена на отрезке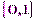 
, поскольку 
монотонно возрастает. Доказано, что если случайная величина h равномерно распределена на отрезке 
, то случайная величина 
имеет функцию распределения 
. Например, для случайной величины, имеющей распределение Лапласа с плотностью вероятностей 
, функция распределения и обратная к ней имеют соответственно вид
Ниже приведен фрагмент рабочего документа Mathcad, содержащий моделирование выборки объема п = 50 случайной величины, имеющей распределение Лапласа с параметрами 
и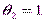 
. В документе представлены гистограмма выборки (рис. 3.3) с графиком теоретической плотности вероятностей, а также график эмпирической функции распределения (рис. 3.4) с графиком теоретической функции распределения.
Рис. 3.3
Рис. 3.4.
Задание 3.2.2