Графовые алгоритмы(33-39)
33.
1) Граф G(V,E) - совокупность двух множеств – непустого множества V (множества вершин) и множества E (множества ребер) неупорядоченных пар различных элементов множества V
G(V,E) = {V,E}, V ¹Æ, EÌV´V, E=E-1.
Число вершин графа G - p, а число ребер – q:
p = p(G) = |V|, q = q(G) = |E|.
2) Пусть v1, v2 – вершины, e=(v1,v2) – соединяющее их ребро. Тогда вершина v1 и ребро e инцидентны, вершина v2 и ребро e также инцидентны. Два ребра, инцидентные одной вершине, называются смежными; две вершины, инцидентные одному ребру, также называются смежными
3) Множество вершин, смежных с вершиной v, называется множеством смежности вершины v и обозначается
Г (v): Г (v) = {uÎV | (u,v)ÎE}
4) Если элементами множества E являются упорядоченные пары, то граф называется ориентированным (или орграфом). В этом случае элементы множества V называются узлами, а элементы множества E – дугами
5) Если элементом множества E может быть пара одинаковых элементов V, то такой элемент E называется петлей, а граф называется графом с петлями (или псевдографом).
6) Если E является не множеством, а набором, содержащим несколько одинаковых элементов, то эти элементы называются кратными ребрами, а граф называется мультиграфом.
7) Если задана функция F:VàM и/или F:EàM, то множество M называется множеством пометок, а граф называется помеченным.
8) Маршрутом в графе называется чередующаяся последовательность вершин и ребер v0,e1,v1,e2,v2,…,ek,vk, в которой любые два соседних элемента инцидентны.
Для обычных графов достаточно просто перечислить либо последовательность вершин либо ребер. Если v0=vk, то маршрут замкнут, в противном случае – открыт. Если все входящие в маршрут ребра различны, то маршрут называется цепью.
9) Длиной маршрута называется количество ребер в нем (с повторениями). Расстоянием между вершинами u и v (обозначается d(u,v)) называется длина кратчайшей цепи {u,v}
10) Две вершины в графе связаны, если существует соединяющая их цепь. Граф, в котором все вершины связаны, называется связным.
Матрица смежности
Это двоичная матрица, кот определяется по правилу:
ì1, если вершина v iсмежна с вершиной v j
M[i,j] = í
î0, если вершины v iи v j не смежны
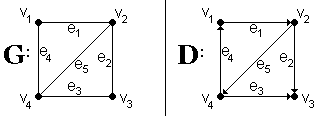
Размер матрицы смежности n(p,q) = O(p2).
G:| 0 1 0 1 | D: | 0 1 0 0 |
| 1 0 1 1 | | 0 0 1 1 |
| 0 1 0 1 | | 0 0 0 0 |
| 1 1 1 0 | | 1 0 1 0 |
Матрица инцидентности
Отражает отношение инцидентности
ì1, если v i инцидентна e j
H[i,j] =  í
í
î0, в противном случае.
Для ориентированного графа используется троичная матрица:
ì1, если v iинцидентна e j и является его концом;
H[i,j] =  í0, если v i не инцидентна e j;
í0, если v i не инцидентна e j;
î-1, если v iинцидентна e j и является его началом.
n(p,q) = O(pq).
G: | 1 0 0 1 0 | D: |-1 0 0 1 0 |
| 1 1 0 0 1 | | 1 -1 0 0 1 |
| 0 1 1 0 0 | | 0 1 1 0 0 |
| 0 0 1 1 1 | | 0 0 –1 –1 1 |
Списки смежности
Представление с помощью списочной структуры, отражающей смежность вершин – список смежности.
 |
В случае представлений неориентиров.графовn(p,q) = O(p+2q), ориентированных – n(p,q) = O(p+q).
37. Массив дуг
Представление графа с помощью массива, содержащего пары смежных вершин, называется массивом ребер (для орграфов – массивом дуг).
| begin | end |
| begin | end |
Для массива ребер (или дуг) оценка n(p,q) = O(2q).
Достижимость и обходы графа
Требуется определить, существует ли путь (задача определения достижимости), ведущий из i-ой вершины в j-ую, а также найти самый короткий и самый длинный.
Проверка достижимости достигается перемножением матриц смежности – каждое следующее перемножение на матрицу смежности приводит к матрице, содержащей пути соответствующей степени.
Обход графа –некоторое систематическое перечисление его вершин (и/или ребер)
39. Алгоритм Дейкстры
Задача: задан ориентированный «взвешенный» граф. Найти кратчайший по длине путь между двумя заданными вершинами.
«Взвешенный» – каждой дуге сопоставлено некотор.отриц.число.

Обозначим через ui кратчайшее расстояние от исходного узла 1 до узла i, через dij - длину ребра (i, j).
Тогда для узла j определим метку [uj, i] следующим образом: [uj, i] = [ui + dij, i], dij >= 0.
Метки узлов могут быть двух типов: временные и постоянные.
Шаг 0. Исходному узлу (1) присваивается метка [0, -]. Полагаем i = 1.
Шаг i. а) Вычисляются временные метки [ui + dij, i] для всех узлов j, которые можно достичь непосредственно из узла i и которые не имеют постоянных меток. Если узел j уже имеет метку [uj, k], полученную от другого узла k, и если ui + dij < uj, тогда метка [uj, k] заменяется на [ui + dij, i].
b) Если все узлы имеют постоянные метки, процесс вычислений заканчивается. В противном
случае выбирается метка [ur, s] с наименьшим значением расстояния ur среди всех временных меток
(если таких меток несколько, то выбор произволен). Полагаем i = r и повторяем шаг i.
Шаг 0. Назначаем узлу 1 постоянную метку [0, -].
Шаг 1. Из узла 1 можно достичь узлов 2 и 3. Вычисляем метки для этих узлов, в результате получаем следующую таблицу меток:
Третий узел имеет наименьшее значение расстояния (u3 = 30). Поэтому статус метки этого узла изменяется на "постоянная".
Шаг 2. Из узла 3 (последнего узла с постоянной меткой) можно попасть в узлы 4 и 5. Получаем следующий список узлов:
Узел Метка Статус метки 1 [0, -] Постоянная 2 [100, 1] Временная 3 [30, 1] Постоянная 4 [30 + 10, 3] = [40, 3] <-Временная 5 [30 + 60, 3] = [90, 3] ВременнаяВременный статус метки [40, 3] узла 4 заменяется на постоянный (u4 = 40).
Шаг 3. Из узла 4 можно достичь узлов 2 и 5. После вычисления меток получим следующий их список:
Узел Метка Статус метки 1 [0, -] Постоянная 2 [40 + 15, 4] = [55, 4] <-Временная 3 [30, 1] Постоянная4 [40, 3] Постоянная 5 [90, 3] или [40+50, 4]=[90,4] ВременнаяВременная метка [100, 1], полученная узлом 2 на втором шаге, изменена на [55, 4]. Это указывает на то, что найден более короткий путь к этому узлу (проходящий через узел 4). На третьем шаге узел 5 получает две метки с одинаковым значением расстояния u5 = 90.
Шаг 4. Из узла 2 можно перейти только в узел 3, но он уже имеет постоянную метку, которую нельзя изменить. Поэтому на данном шаге получаем такой же список меток, как и на предыдущем шаге, только метка узла 2 получает статус постоянной.
Шаг 5. С временной меткой остается только узел 5, но так как из этого узла нельзя попасть ни в какой другой, ему присваивается постоянный статус и процесс вычислений заканчивается.

Кратчайший маршрут между узлом 1 и любым другим узлом определяется начиная с узла назначения путем прохождения их в обратном направлении с помощью информации, представленной в постоянных метках.
(2) -> [55, 4] -> (4) -> [40, 3] -> (3) -> [30, 1] ->(1)Между узлами (2) и (1): [55, 4].