Производная по направлению. Градиент.

Рассмотрим функцию трех переменных u=f(x,y,z). Пусть она определена в некоторой окрестности точки Мо(хо,yo,zo). Рассмотрим всевозможные лучи, выходящие из точки Мо. Каждый такой луч заадется единственным вектором (соsa, cosb,cosg). Если l- длина этого отрезка, то его координаты (lcosa, lcosb, lcosg) C другой стороны: (x-xo, y-yo, z-zo)

Т.о. получили один и тот же отрезок:

Приравняем

u=f(Xo+lcosa, Yo+lcosb, Zo+lcosg) (1)

Т.о. u- сложная функция.

Производную указанной сложной функции по переменной l, взятую в точке l=0 нназывают производной функции u=f(x,y,z) в точке Мо по направлению, оопределяемому единичным вектором l. Обозначение:

(2)

Градиентом функции u=f(x,y,z) в данной точке Мо(xo,yo,zo) называется вектор, координаты которого имеют вид gradu(Mo)=

Если: u=f(x1,x2,…,xn) Mo(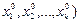

[Т] Вектор градиента функции y=f(x,y,z) в точке Мо характеризует направление и величину максимального роста функции в точке Мо,т.е. производные функции u=f(x,y,z) в точке Мо по направлению, определенному вектором градиента этой функции в точке Мо имеет максимальное значение по сравнению с производной по любому другому направлению и это значение равно длине вектора градиента.

Док-во: Из ф-л (1) и(2) →(gradu,e) =∂u/∂e

∂u/∂e=(gradu,e) = |gradu|*|e|*cosφ

Cosφ=1 φ=0

Max значение достигается ↔ вектор е и вектор grad направлены одинаково. Тогда |∂u/∂e=gradu|

Следствие. Вектор градиента не зависит от выбора координат.

Геометрический смысл градиента:

Линии уровня для функции двух переменных u=f(x,y) называется линия на которой функция сохраняет свое постоянное значение.

Если В каждой точке линии уровня M(xо,yо) построить касательную, то вектор-градиент в точке Мо будет перпендикулярен этой касательной.

Поверхность уровня- фунция u=f(x,y,z) в точке Мо (xo,yo,zo) называется поверхность на которой функция сохраняет свое постоянное значение.

Свойства: если в каждой точке Mo(xo,yo,zo) провести касательную поверхность, то вектор градиент будет ортогонален этой поверхности.

Частные производные высших порядков функции N переменных.

Пусть u=f(x) диф в окрестной точке х0,значит в окр точке сущ. частные производные Пусть частные производные сущ. в каждой точке области D ∂u/∂x_i=di=1,n, если она сущ в каждой обл D то её можно рассматривать как некоторую функцию нескольких переменных, заданных на обл D следовательно у неё существуеют частные производные d'u/d'xi, i=1,...,n: d'/d'xk(d'u/d'xi)=d^2u/(d'xid'xk)

Частная производная взятая от d'u/d'xi, i=1,...,n по переменной Хк называется частной производной второго порядка и обозначается d'^2u/d'xid'xk, i=1,...,n шне равно к, если I=k, то она обозначается как d'^2u/d'xi^2

Смешанные частные производные второго порядка для непрерывной функции равны. Аналогично, равные смешанные частные производные 3, 4 и т.д.

Теорема.Пусть ф-я диф к-раз в точке х0,то в этой точке значение любой смешанной частной производной к-го порядка(последовательности), где происходят последовательное диф, т.е. ∂²u/∂x_i∂x_j =∂²u/∂x_i∂x_j