Пусть λ=max∆I – длина наиб. Частичнго отрезка λ→0.
Если существует конечный предел I интегральных сумм s при l®0, то этот предел называется определенным интегралом Римана для функции f(x) по отрезку [a,b] и обозначается I= 
= 
(**)
D'ef функция f(x) называется интегрируемой на [a,b] если для любой последовательности разбиений {Xk}, у которой 
соответствующая последовательность интегральных сумм {sk} стремится к одному и тому же числу I.
D'ef Число I называется определенным интегралом по Риману для функции f(x) оп отрезку [a,b], если для любого e>0 сущесвтует такое d>0, что при l<d (т.е. если отрезок [a,b] разбит на части с длинами DXi<d) независимо от выбора точек xI выполняется неравенство 
, или же 
Замечание.Число I называется определенным интегралом Римана от функции f(x) по сегменту [a,b] и обозначается так: I= 
, где а- нижний предел, b- верхний предел
Следует отметить, что 
= 
= 
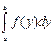
Услоловия сущ-ия опр интеграла.Суммы Дарбу.Необход и достат условия.
Основные свойства определенного интеграла.
1. 1. 
=0
Если а>b, то по определению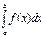 
= - 
(4), т.е. когда отрезок [a,b] при a<b пробегает в направлении от b к а, имеем b=X0, а=Xn, DXi=Xi-Xi-1<0
2. 2. = 
+ 
(здесь и в дальнейшем предполагается, что интегралы, входящие в доказываемые формулы существуют)
Доказательство: Допустим сначала, что а<c<b, т.к. предел интегральной суммы s не зависит от способа разбиения отрезка [a,b], то будем проводить разбиение так, чтобы точка с всегда была бы точкой разбиения [a,b]. Если например с=хm, то s можно разбить на две суммы: s= 
= 
+ 
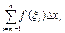. Переходя в последнем равенстве к пределу при l®0 мы и получим искомое равенство.
Суть доказанного свойства состоит в том, что определенный интеграл по всему отрезку равен сумме интегралов по его частям.
Доказательство для другого расположения точек a, b, c легко сводится к рассмотренному случаю. Пусть, например, а<b<c, тогда по доказанному, имеем: 
= 
+ 
, откуда учитывая (4) получаем = 
- 
= 
+ 
, ч.т.д.
3. Постоянный множитель можно выносить за знак определенного интеграла, т.е. 
=к . Доказательство: действительно, для любого разбиения отрезка [a,b] и любого выбора точек xI 
=k 
Переходя к пределу при l®0 имеем = 
= 
=к 
= к ., ч.т.д.
4. Определенный интеграл от алгебраической суммы функций равен алгебраической сумме их интегралов, т.е. 
± 
. Доказательство: действительно, для любого разбиения отрезка [a.b] и любого выбора точек xI 
= 
± 
Так как 
= и 
= 
, то получаем что 
= 
± 
= 
± 
Оценки интегралов. Формула среднего значения.
[Т] Если функция f(x) непрерывна на сегменте [a,b] то существует т С, принадлежащая этому сегменту, такая что =f(c)(b-a). Эта формула называется формулой среднего значения.
Замечание: теорема о среднем имеет четкий геометрический смысл: величина определенного интеграла при f(x)>=0 равна площади прямоугольника имеющего высоту f(c) и основание b-a.
[Т] Пусть а<в.
· Если f(x)≥0 для любого х?[a,b]→∫от а до в f(x)≥0
· Если f(x) ≥g(x) для любого х?[a,b]→∫f(x)dx≥∫g(x)dx
· Если f(x) опред на [a,b]→|∫f(x)dx|≤∫f(x)dx
· Если |f(x)|≤k для любого х?[a,b]→|∫f(x)dx|≤k*(b-a)
· Пусть m,M соответств наим и наиб значения ф-ии f(x) на [a,b],тогда справедлива ф-ла m(b-a)=∫f(x)dx≤M(b-a)