Проведем анализ полученного решения на чувствительность.

Домашнее задание

РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ГРАФИЧЕСКИМ МЕТОДОМ И АНАЛИЗ РЕШЕНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ

Предприятие выпускает 2 вида изделий, используя при этом 4 вида ресурсов. Известно распределение ресурсов на каждую единицу производимой продукции, а также величина выручки, получаемая от реализации одной единицы изделия.

Примем следующие обозначения:

i – номер вида ресурса (i =1,4);

j – номер вида изделия (j =1,2);

a_ij – распределение i -го вида ресурса на единицу производимой продукции j -ого вида;

b_i – запасы ресурсов;

(x₁, x₂,) – искомый план производства.

Нормы расхода ресурсов на изготовление 1 единицы изделия и выручка от реализации 1 единицы продукции приведены в таблице:

Ресурс	Нормы расхода ресурсов на изготовление 1 единицы изделия	Запас ресурса
I	II
	a11	a12	b1
	a21	a22	b2
	a31	a32	b3
	a41	a42	b4
Выручка от реализации 1 единицы изделия, ден.ед.	c1	c2

Задание:

1. Составить математическую модель задачи, позволяющую определять оптимальный план производства изделий.

2. Решить задачу графическим методом.

3. Провести анализ полученного решения на чувствительность:

- анализ изменения запасов ресурсов;

- определение наиболее выгодного ресурса;

- анализ изменения коэффициентов целевой функции.

ВАРИАНТЫДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ

«АНАЛИЗ МОДЕЛИ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

НА ЧУВСТВИТЕЛЬНОСТЬ»

(номер варианта соответствует номеру в списке группы)

№

с 1

с 2

а 11

а 12

а 21

а 22

а 31

а 32

а 41

а 42

b 1

b 2

b 3

b 4

 

Типовой вариант решения задачи:

Составление математической модели задачи (описать самостоятельно).

Решим задачу графическим методом.

z = 2 x₁ + 3 x₂ à max

при ограничениях

Область допустимых решений (ОДР) задачи – замкнутая многоугольная область OABDO (рис.1). Максимум целевой функции достигается в точке В, которая находится на пересечении прямых, соответствующих ограничениям 1 и 2. Её координаты находим решая совместно систему уравнений этих прямых:

Откуда, х ₁= 1, х ₂ = 2,5.

Значение целевой функции в точке В: z = 2 x₁ + 3 x₂ = 2 * 1 + 3 * 2,5 = 9,5.

 

Проведем анализ полученного решения на чувствительность.

Задача 1. Анализ изменения запасов ресурсов

В нашем примере связывающими ограничениями являются 1 и 2, несвязывающими – 3 и 4. Дефицитными тогда являются ресурсы 1 и 3, недефицитными – 3 и 4.

 

Рассмотрим сначала дефицитные ресурсы. Проанализируем, насколько можно увеличить их запас, чтобы некоторым образом улучшить оптимальное решение.

 

Ресурс 2. При увеличении запаса этого ресурса прямая 2 перемещается вверх, параллельно самой себе до точки М (рис.2), в которой пересекаются линии ограничений 1 и 4. В этой точке эти ограничения становятся связывающими. А точка М становится новым оптимальным решением. Дальнейший рост запаса этого ресурса не будет влиять ни на область решений, ни на оптимальное решение.

Новое решение, т.е. координаты точки М, найдем, решая совместно систему уравнений прямых, соответствующих ограничениям 1 и 4:

. Откуда х ₁= 5, х ₂ = 0,5, т.е. М (5, 0,5).

Подставляем координаты т. М в левую часть ограничения 2, определяем максимально допустимый запас ресурса 2:

5 x₁ + 2 x₂ = 5 * 5 + 2 * 0,5 = 26.

Таким образом, новое ограничение 2 будет иметь вид: .

Значение целевой функции в точке М будет:

z (М) = 2 x₁ + 3 x₂ = 2*5+3*0,5 = 11,5.

 

Ресурс 1. При увеличении запаса этого ресурса прямая 1 перемещается вверх, параллельно самой себе до точки N (рис.3), в которой пересекаются линии ограничений 2 и 3. В этой точке эти ограничения становятся связывающими. А точка N становится новым оптимальным решением.

Координаты точки N, найдем, решая совместно систему уравнений прямых, соответствующих ограничениям 2 и 3:

. Откуда х ₁= 0,4, х ₂ = 4, т.е. N (0.4, 4).

Подставляем координаты т. N в левую часть ограничения 1, определяем максимально допустимый запас ресурса 1:

3x₁ + 6 x₂ =3*0,4 + 6*4 = 25,2.

Таким образом, новое ограничение 2 будет иметь вид: .

Значение целевой функции в точке N будет:

z (N) = 2 x₁ + 3 x₂ = 2*0,4 + 3*4 = 12,8.

 

Теперь рассмотрим несвязывающие ограничения (недефицитные ресурсы).

Из рис.4 видно, что не изменяя оптимального решения, прямые, соответствующие ресурсам 3 и 4 можно перемещать до пересечения с оптимальной точкой В.

Точка В имеет координаты (1, 2.5), отсюда уменьшение запаса ресурса 3 произойдет с 4 единиц до 2,5, а четвертого ресурса – с 5 единиц до 1.

Тогда, новые ограничения 3 и 4 будут иметь вид: .

Изменение запасов недефицитных ресурсов не повлияет на значение целевой функции.

 

Сведём полученные данные в таблицу:

Ресурс	Вид ресурса	Max изменение запаса ресурса	Max изменение значения целевой функции
	дефицитный	25,2 – 18 = +7,2	12,8 – 9,5 = 3,3
	дефицитный	26 – 10 = +16	11,5 – 9,5 = 2
	недефицитный	2,5 – 4 = - 1,5
	недефицитный	1 – 5 = - 4

 

Задача 2. О пределение наиболее выгодного ресурса.

 

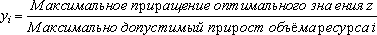
В нашем примере ценность единицы каждого дефицитного ресурса будет следующей:

 

_{, .}

 

Из результатов следует, что дополнительные вложения должны быть направлены, в первую очередь, на увеличение 1 ресурса.

 

Задача 3. О пределение пределов изменения коэффициентов целевой функции.

 

При изменении коэффициентов целевой функции, линии уровня изменяют свой наклон. При варьировании этих коэффициентов можно изменить совокупность связывающих ограничений, что, в свою очередь, может привести к изменению статуса того или иного ресурса.

 

Будем исследовать 2 момента:

- диапазон изменения коэффициентов целевой функции, при котором не происходит изменения оптимального решения;

- величины, на которые нужно изменить коэффициенты целевой функции, чтобы изменить статус ресурса.

 

При увеличении с ₁ или уменьшении с ₂ – линия уровня вращается по часовой стрелке вокруг оптимальной точки.

 

При уменьшении с ₁ или увеличении с ₂ – линия уровня вращается против часовой стрелки (рис. 5).

 

Таким образом, точка В будет оставаться оптимальной до тех пор, пока наклон линии уровня не выйдет за пределы, определяемые наклонами прямых связывающих ограничений 1 и 2.

Если коэффициент угла наклона линии уровня k_z станет равным коэффициенту угла наклона прямой, соответствующей первому ограничению k ₁, получим альтернативный оптимум, содержащий все значения отрезка АВ.

Если k_z станет равным k ₂, получим альтернативный оптимум, содержащий все значения отрезка ВD.

 

Наличие альтернативных оптимумов говорит о том, что одно и то же оптимальное значение может достигаться при варьировании переменных х ₁ и х ₂.

При выходе наклона линии уровня за пределы выявленного интервала, получится некоторое новое оптимальное решение.

 

Найдём допустимый интервал изменения с ₁, при котором точка В останется оптимальной.

Исходное значение с ₂ = 3 оставим без изменения.

Уменьшаем значение с ₁ до тех пор, пока линия уровня не совпадет с прямой АВ (1). Тогда их коэффициенты угла наклона станут равными друг другу: k_z = k ₁.

_{, .}

Приравниваем значения _, откуда получаем с _min = 3/2.

 

Увеличиваем значение с ₁ до тех пор, пока линия уровня не совпадет с прямой BD (2). Тогда их коэффициенты угла наклона станут равными друг другу: k_z = k ₂.

_{, .}

Приравниваем значения _, откуда получаем с _max = 15/2.

Искомый диапазон изменения коэффициента .

 

Найдём допустимый интервал изменения с ₂, при котором точка В останется оптимальной.

Исходное значение с ₁ = 2 оставим без изменения.

Уменьшаем значение с ₂ до тех пор, пока линия уровня не совпадет с прямой BD (2). Тогда их коэффициенты угла наклона станут равными друг другу: k_z = k₂.

_{, .}

Приравниваем значения _, откуда получаем с _min = 4/5.

Увеличиваем значение с ₂ до тех пор, пока линия уровня не совпадет с прямой AB (1). Тогда их коэффициенты угла наклона станут равными друг другу: k_z = k ₁.

_{, .}

Приравниваем значения 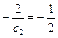_, откуда получаем с _max = 4.

Искомый диапазон изменения коэффициента .