ОЦЕНКИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

 

ДОНЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

ЭЛЕКТРОТЕХНИЧЕСКИЙ ФАКУЛЬТЕТ

 

КАФЕДРА ЭЛЕКТРОПРИВОДА И АВТОМАТИЗАЦИИ ПРОМЫШЛЕННЫХ УСТАНОВОК

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО ДИСЦИПЛИНЕ

ОСНОВЫНАУЧНЫХ ИССЛЕДОВАНИЙ

 

 

ДОНЕЦК ДонГТУ 2000

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

 

ДОНЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

ЭЛЕКТРОТЕХНИЧЕСКИЙ ФАКУЛЬТЕТ

 

КАФЕДРА ЭЛЕКТРОПРИВОДА И АВТОМАТИЗАЦИИ ПРОМЫШЛЕННЫХ УСТАНОВОК

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

 

К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ ПО ДИСЦИПЛИНЕ

ОСНОВЫНАУЧНЫХ ИССЛЕДОВАНИЙ

(для студентов специальности 7.0922.03)

 

 

Рекомендовано к изданию

методической комиссией

специальности ЭАПУ

(Протокол № от 2000)

 

ДОНЕЦК ДонГТУ 2000

 

УДК 608 (075.8)

 

Методические указания к практикуму дисциплины «Основы научных исследований для студентов специальности 7.0922.03» / Сост. Н.С Никорюк., И.С. Стеценко– ДонГТУ. 1999. - кол-во стр 66.

 

 

В указаниях изложена методика обработки данных и планирования эксперимента. Приведены расчеты примеров по каждому разделу дисциплины. Даны задания для самостоятельной работы студентов.

 

 

Составители: Н.С. Никорюк, доцент

И. С. Стеценко, студент

Отв. за выпуск П.Х. Коцегуб, зав кафедрой

Рецензент В.А. Эсауленко, профессор

 

Рекомендовано к изданию в электронном варианте учебно-методическим советом ДонГТУ. Протокол № от 2000г.

 

 

Оглавление

Вступление.............................................................................. 5 стр.

Оценки погрешностей измерения

1.1 Основные определения и формулы................................. 6 стр.

1.2 Примеры к практическому занятию по оценке

погрешностей измерения.................................................. 10 стр.

1.3 Задачи для самостоятельного решения........................... 15 стр.

Метод наименьших квадратов

2.1 Методические указания к первому занятию

по методу наименьших квадратов.................................... 18 стр.

2.2 Примеры к первому практическому занятию................. 20 стр.

2.3 Задачи для самостоятельного решения на первом

практическом занятии....................................................... 27 стр.

2.4 Методические указания ко второму практическому

занятию.............................................................................. 28 стр.

2.5 Примеры ко второму практическому занятию

по методу наименьших квадратов.................................... 30 стр.

2.6 Задачи для самостоятельного решения на втором

занятии............................................................................... 35 стр.

3. Методы планирования эксперимента

3.1 Методические указания к первому занятию.................... 37 стр.

3.2 Примеры к первому практическому занятию................. 42 стр.

3.3 Задачи для самостоятельного решения на первом

практическом занятии....................................................... 46 стр.

3.4 Методические указания ко второму практическому

занятию.......................................................................... 47 стр.

3.5 Примеры ко второму практическому занятию............... 52 стр.

3.6 Задачи для самостоятельного решения на втором

занятии............................................................................... 59 стр.

Приложение............................................................................ 61 стр.

Список рекомендуемой литературы...................................... 66 стр.

 

ВСТУПЛЕНИЕ

Методические указания предназначены для студентов специальности "Электропривод и автоматизация промышленных установок и технологических комплексов" (ЭАПУ), изучающих дисциплину "Основы научных исследований".

Цель данных указаний состоит в том, чтобы показать на сравнительно простых примерах методику статической обработки данных и планирования эксперимента, облегчить студентам изучение материала курса.

Каждый раздел содержит основные положения и разъяснения соответствующих вопросов изучаемого курса, которые иллюстрируются численными расчетами простых примеров. В конце каждого раздела даны задачи для организации самостоятельной работы студентов.

 

 

ОЦЕНКИ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ

 

1.1 Основные определения и формулы

 

Разность Dх между результатом измерения х и истинным значением измеряемой величины х₀ называется абсолютной погрешностью результата измерения:

 

Dх = х – х₀. (1.1)

 

Погрешность Dх является случайной величиной. Она может быть представлена в виде

 

Dх = Dх_с – , (1.2)

 

где Dх_с - математическое ожидание величины Dх, а - случайная величина с нулевым математическим ожиданием. Неслучайную величину Dх_с называют систематической погрешностью, - случайной погрешностью. Если значение Dх_с известно, то систематическую погрешность можно исключить, приняв за окончательный результат измерения х_испр - исправленный результат измерения:

 

х_испр = х – Dх_с . (1.3)

 

Для оценки влияния погрешности на результат измерения задаются погрешностями Dх₁ и Dх₂ и находят вероятность того, что измеряемая величина х заключена между (х – Dх₂) и (х + Dх₁). Интервал [х – Dх₂; х + Dх₁] называется доверительным интервалом, а вероятность того, что х находится внутри этого интервала, - доверительной вероятностью Р_Д. Это может быть записано в следующем виде

 

. (1.4)

 

Обычно выбирают . Тогда

 

. (1.5)

 

Если известен дифференциальный закон распределения погрешности Dх, т.е. плотность вероятности f(Dх), то

 

. (1.6)

Числовые характеристики закона распределения f(Dx) – математическое ожидание Dх_с, дисперсия D и среднее квадратичное отклонение s – могут быть определены по формулам

 

; (1.7)

 

; (1.8)

 

. (1.9)

 

При нормальном законе распределения погрешностей

 

. (1.10)

 

В этом случае, пользуясь таблицей функции Лапласа Ф(Z) (см. приложение 4), можно определить

 

. (1.11)

 

При использовании приложения 4 необходимо учитывать

 

Ф(–Z) = – Ф(Z). (1.12)

 

В ряде случаев закон распределения погрешностей не известен, однако известны (обычно приближенно) его числовые характеристики Dх_с и s. Тогда для грубой оценки снизу доверительной вероятности Р_Д при заданном симметричном доверительном интервале Dх₁ можно воспользоваться неравенством Чебышева

 

. (1.13)

Тогда

 

. (1.14)

Если случайная величина У связана с независимыми случайными величинами У₁, У₂,…,У_n известной функциональной зависимостью У = F(У₁, У₂,…,У_n), то, зная математические ожидания m_y1, m_y2,…, m_yn и средние квадратичные отклонения s_y1, s_y2,…s_yn величин У₁, У₂,…,У_n, можно приближенно найти математическое ожидание m_y и среднее квадратическое отклонение s_y величины У по формулам

 

m_y = F(m_y1, m_y2,…m_yn); (1.15)

 

, (1.16)

 

где - частная производная функции F(У₁, У₂,…,У_n) по y_i, взятая в точке (m_y1, m_y2,…m_yn).

 

Если У₁, У₂,…,У_n - случайные результаты прямых независимых измерений различных физических величин, а У = F(У₁, У₂,…,У_n) - результат косвенного измерения, тогда среднее квадратическое отклонение s случайной погрешности результата косвенного измерения можно найти по формуле

 

, (1.17)

 

где - среднее квадратическое отклонение случайной погрешности результата прямого измерения У_i, а частная производная берется в точке У₁, У₂,…,У_n, соответствующей результатам прямых измерений.

Систематическая погрешность Dх_с результата косвенного 膆††††††††††††††††††††††††††††††††††††††††††††††††D†_††††D†_††††††D†_††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††††ного значения х и получены результаты х₁, х₂,…,х_n, то

 

, (1.19)

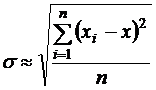. (1.20)

 

При неизвестной величине х (произведено n независимых наблюдений одного и того же неизвестного значения) найти оценку систематической погрешности Dх_с невозможно. Если пренебречь систематической погрешностью, то в качестве оценки истинного значения измеряемой величины следует принять среднее арифметическое результатов наблюдений:

 

. (1.21)

 

Среднее квадратическое отклонение величины х_ср равно

 

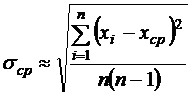. (1.22)

 

Среднее квадратическое отклонение каждого отдельного наблюдения, характеризующее точность метода измерения

 

. (1.23)

 

Оценка систематической погрешности

 

. (1.24)

 

Если известно, что погрешности отдельных наблюдений распределены по нормальному закону (параметры которого неизвестны), то вместо приближенной формулы (1.24) следует использовать точное выражение

 

, (1.25)

 

где - интегральная функция распределения Стьюдента (см. приложение 5). Выражение (1.25) справедливо для любых n>1.

Если число наблюдений n мало (n<10¸20), а закон распределения погрешностей отдельных наблюдений нельзя считать близким к нормальному, то применение выражения (1.24) приводит к значительным погрешностям. В этом случае для грубой оценки величины Р_Д имеет смысл использовать выражение (1.14), положив в нем s = s_ср.

Если ряд наблюдений х₁, х₂,…, х_n содержит результат х_k, существенно отличающийся от остальных, то необходимо проверить, не является ли он промахом. При нормальном законе распределения отдельных результатов измерения x_i обнаружение промаха сводится к проверке

 

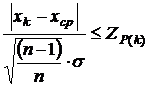, (1.26)

 

при известной дисперсии или

 

, (1.27)

 

при неизвестной дисперсии.

В этих выражениях - граница доверительного интервала нормально распределенной величины Z при доверительной вероятности p­ⁿ; - граница доверительного интервала случайной величины , имеющей специальное распределение (приложение 6), зависящее от n, при доверительной вероятности Р. Если неравенства (1.26) и (1.27) не выполняются, то x_k следует считать промахом. Его необходимо исключить из ряда наблюдений, и для оценки результата измерения необходимо заново пересчитать x_cp и s_cp.

 

1.2 Примеры к практическому занятию по оценке погрешностей измерения

 

Пример 1.1. Имеются результаты девяти измерений (m=9) случайной величины х, распределенной по нормальному закону: -1,8; 1,2; -0,5; -0,8; 2,3; -1,5; 2,3; 1,7; -0,25. Определить значение и доверительный интервал (погрешность измерения) при уровне значимости p = 1 - b = 0,05.

В соответствии с выражениями (1.23), (1.21)

 

, где .

Используем фрагмент математико-статической таблицы (см. приложе- ние 3) со значениями величины t=f(r) при уровне значимости 0,05 (доверительной вероятности 95%):

 

r												¥
t	12,71	4,30	3,18	2,78	2,45	2,31	2,23	2,13	2,09	2,04	1,98	1,96

 

При числе степеней свободы r = n–1=8 найдем, что t=2,31. В соответствии с выражением (1.22) среднеквадратичное отклонение в определении истинного значения m_x

 

.

 

Тогда погрешность измерения

 

.

 

Таким образом, с вероятностью b=0,95 истинное значение величины х0 лежит в пределах

 

,

или

.

 

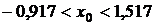Пример 1.2. При измерении величины х получена такая последовательность числовых значений: 123,5; 124,1; 123,8; 125,0; 135,2; 126,1. В приведенной последовательности вызывает сомнение результат пятого измерения. Найдем значение v, соответствующее этому измерению

 

;

;

.

 

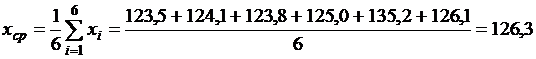Тогда в соответствии с формулой (1.26)

 

.

 

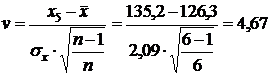Воспользуемся значениями величины v^T=f(n) при уровне значимости 0,05

 

n
vT	1,41	1,69	1,79	2,00	2,17	2,29	2,39	2,46	2,52	2,58	2,62

 

Для n=6 находим v^T=2,00. Так как v>v^T, результат пятого измерения (x₅=135,2) следует отнести к промаху и исключить из рассмотрения. Тогда найдем новые значения статических оценок (по результатам пяти измерений):

 

; .

 

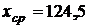Среднеквадратичное отклонение при определении математического ожидания, вычисленное в соответствии с выражением (1.3)

 

.

 

Воспользовавшись фрагментом таблицы к примеру 1.1, при r = n–1=4 получим t=2,78. Следовательно, погрешность серии из пяти измерений

 

;

и

.

 

Заметим, что сохранение промаха в серии из шести опытов при том же уровне значимости р=0,05 дает следующий результат: x=126,3±5,43, т.е. имеет существенное отклонение среднего значения измеряемой величины и особенно погрешности измерения.

 

Пример 1.3. Погрешность измерения DU распределена по нормальному закону, причем систематическая погрешность DU_c равна нулю, а sср равно 50 мВ.

Найдите вероятность того, что результат измерения U отличается от истинного значения напряжения не более чем на 120 мВ.

Из выражения (1.11) при

 

DU_c=0 иDU₁=DU₂=120 мВ

следует, что

 

,

 

.

 

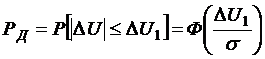Воспользовавшись приложением 4, получим

 

и

 

.

 

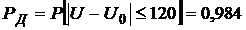Пример 1.4. Решите задачу 1.3 при условии, что систематическая погрешность DU_c равна 30 мВ.

Если в результате измерения U не вносить поправку, учитывающую систематическую погрешность, то для нахождения искомой вероятности можно воспользоваться соотношением (1.1):

 

 

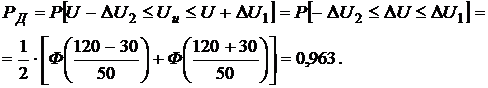
Если в результат измерения U внести поправку, т.е. считать, что

 

 

то

 

 

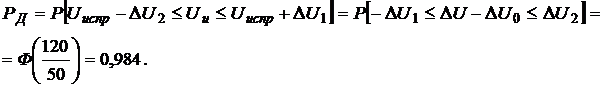
Сравнивая результаты, полученные в примере 1.3 и 1.4, нетрудно заметить, что для нормального закона распределения погрешностей при одинаковом доверительном интервале доверительная вероятность больше в том случае, когда DU_c равна нулю или внесена соответствующая поправка в результат измерения.

Пример 1.5. Погрешности результатов измерений, произведенных с помощью амперметра, распределены по нормальному закону; sср равно 20 мА, систематической погрешностью можно пренебречь. Сколько независимых измерений нужно сделать, чтобы хотя бы для одного из них погрешность не превосходила ±5 мА с вероятностью не менее 0,95?

 

Вероятность того, что при одном измерении погрешность не превысит ±5 мА, равна

 

.

 

Вероятность того, что при n независимых измерениях ни одно из них не обеспечит погрешности, меньшей ±5 мА, равна

 

.

 

Но с другой стороны, эта же вероятность должна быть не более

 

1 – 0,95 = 0,05.

Следовательно,

,

откуда

.

 

Так как число измерений n может быть только целым, то

 

.

 

Пример 1.6. Измерительный усилитель построен на базе операционного усилителя путем применения параллельной отрицательной обратной связи по напряжению (рисунок 1.1).

 

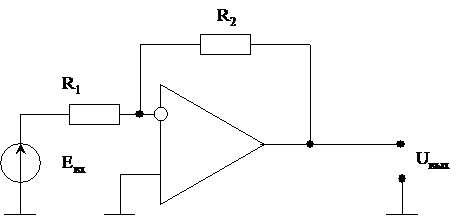
Рисунок 1.1

 

Математические ожидания и средние квадратические отклонения сопротивлений R₁ и R₂ цепи отрицательной обратной связи известны: m₁=1кОм; m₂=10 кОм; s₁=1 Ом; s₂=10 Ом. Считая операционный усилитель идеальным (бесконечно большой коэффициент усиления, бесконечно большое входное и бесконечно малое выходное сопротивления), определите математическое ожидание и среднее квадратическое отклонение s_k коэффициента усиления измерительного усилителя.

Можно показать, что в рассматриваемом случае коэффициент усиления по напряжению К измерительного усилителя равен

 

.

Согласно (1.15)

.

 

Согласно (1.16)

 

 

 

1.3 Задачи на самостоятельную проработку

 

Задача 1.1. Произведен ряд независимых наблюдений напряжения:

 

№ наблюдения
U, мВ

 

Предполагая, что систематической погрешностью можно пренебречь, определите оценку истинного значения измеряемого напряжения U0 и доверительный интервал (погрешность измерения) при уровне значимости р=0,05.

 

Задача 1.2. В задаче 1.1 найдите приближенно: доверительную вероятность того, что истинное значение измеряемого напряжения U₀ отличается от U_ср не более чем на 30 мВ.

 

Задача 1.3. В задаче 1.1 найдите оценки систематической погрешности DU_c и среднеквадратичное отклонение s, если известно, что истинное значение измеряемого напряжения равно 3805 мВ.

 

Задача 1.4. В задаче 1.1, предполагая, что погрешности наблюдений распределены по нормальному закону с нулевым математическим ожиданием, найдите: доверительную вероятность того, что истинное значение измеряемого напряжения U₀ отличается от U_ср не более чем на 30 мВ; симметричный доверительный интервал DU, соответствующий доверительной вероятности 0,95.

 

Задача 1.5. В задаче 1.1 найдите приближенно вероятность того, что истинное значение измеряемого напряжения заключено между 3780 и 3830 мВ. Найдите эту вероятность точно, если априори известно, что закон распределения погрешностей - нормальный.

 

Задача 1.6. Усилитель построен на базе операционного усилителя путем применения последовательной обратной отрицательной связи по напряжению (рисунок 1.2). Математические ожидания и средние квадратические отклонения сопротивлений R₁ и R₂ цепи отрицательной обратной связи известны: m₁=10 Ом; m₂=990 Ом; s₁=0,01 Ом; s₂=1 Ом. Считая операционный усилитель идеальным, определите математическое ожидание и среднее квадратическое отклонение коэффициента усиления усилителя.

 

Рисунок 1.2

 

Задача 1.7. Коэффициент усиления К усилителя определяется выражением

 

,

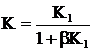где - коэффициент усиления операционного усилителя; b - коэффициент передачи цепи отрицательной обратной связи.

Математическое ожидание и среднее квадратическое отклонение величины соответственно равны 10⁴ и 10³. Найдите математическое ожидание и среднее квадратическое отклонение величины К при условии, что b=10^-2.

 

Задача 1.8. Решите задачу 1.7 при условии, что b - случайная величина, причем m_b=10^-2, a s_b=10^-4.

 

Задача 1.9. Усилитель построен по схеме, показанной на рисунке 1.1. Операционный усилитель имеет дрейф нуля. Эквивалентная схема усилителя приведена на рисунке 1.3.

Известны математические ожидания и средние квадратические отклонения выходных параметров источников тока и ЭДС, определяющих дрейф m_I=1 мкА; m_E=1 мВ; s_I=1 мкА; s_E=1 мВ. Определите математическое ожидание m и среднее квадратическое отклонение s выходного напряжения усилителя (при отсутствии входного напряжения), считая операционный усилитель идеальным, причем R₁=1 кОм; R₂=10 кОм.

 

 

Рисунок 1.3

 

Задача 1.10. Известны математические ожидания и средние квадратические отклонения сопротивлений R₁ и R₂: m₁=10 Ом; m₂=20 Ом; s₁=0,10 Ом; s₂=0,14 Ом. Найдите математическое ожидание и среднее квадратическое отклонение отношения сопротивлений последовательного соединения R₁ и R₂ и параллельного.