Прямая на плоскости.
Каждая прямая на плоскости Oxy определяется линейным уравнением первой степени с двумя неизвестными. Обратно: каждое линейное уравнение первого порядка с двумя неизвестными определяет некоторую прямую на плоскости.
1. Уравнение прямой с угловым коэффициентом имеет вид
y=kx+b, (2.1)
Где k-угловой коэффициент прямой (т.е. тангенс угла a, который прямая образует с положительным направлением оси Ox, k=tga), b- ордината точки пересечения прямой с осью Oy.
2. Общее уравнение прямой:
Ax+By+C=0, (2.2)
Где A,B,C-постоянные коэффициенты, причем А и В одновременно не обращаются в нуль(А2+В2¹ 0).
Заметим, что n=(A;B)- нормальный вектор прямой (n перпендикулярен прямой).Частные случаи этого уравнения:
Ax+By=0 (C=0)-прямая проходит через начало координат;
Ax+C=0 (B=0) -прямая параллельна оси Oy;
By+C=0 (A=0) - прямая параллельна оси Ox;
Ax=0 (B=C=0) -прямая совпадает с осью Oy;
By=0 (A=C=0) - прямая совпадает с осью Ox.
3. Уравнение прямой в отрезках:
 +
+  =1, (2.3)
=1, (2.3)
где aи b длины отрезков (с учетом знаков),отсекаемых прямой на осях Ox и Oy соответственно (рис 23).
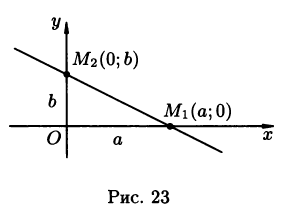
4. Уравнение прямой проходящей через данную точку в данном направлении:
y-y0=k(x-x0), (2.4)
где k=tga (a-угол образуемый прямой с осью Ox); (x0;y0)- координаты данной точки. Уравнение (2.4) называют также уравнением пучка прямых с центром в точке (x0;y0);уравнение пучка прямых, проходящих через точку пересечения двух прямых A1x+B1y+C1=0 и A2x+B2y+C2=0 имеет вид:
A1x+B1y+C1+ l(A2x+B2y+C2)=0,(2.5)
Где l-числовой множитель.
5. Уравнение прямой, проходящей через две данные точки М1(x1;y1) и М2(x2;y2),где y1=/y2, x1=/x2 имеет вид 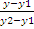 =
= 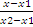 .
.
Угловой коэффициент прямой, проходящей через две данные точки определяется по фопмуле
K =  .
.
Если x1=x2, то уравнение прямой (2.6) имеет вид x=x1; если y1=y2, то: y=y1.
6. Нормальное уравнение прямой.
x 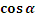 +y
+y 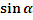 -p=0, (2.8)
-p=0, (2.8)
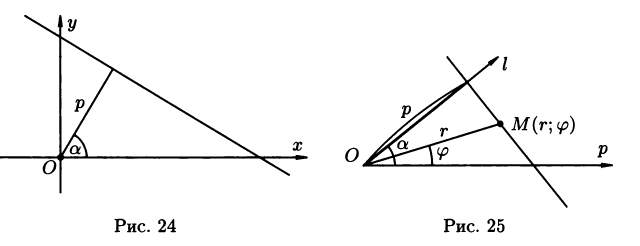
где p- длинна перпендикуляра, опущенного из начала координат на прямую,a - угол,который этот перпендикуляр образует с положительным направлением оси Ох (рис.24)
Общее уравнение прямой (2.2) можно преобразовать в нормальное уравнение (2.8) путём умножения на нормирующий множитель l= 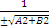 ; знак перед дробью берётся противоположный знаку свободного члена С(в общем уравнении прямой).
; знак перед дробью берётся противоположный знаку свободного члена С(в общем уравнении прямой).
7. Уравнение прямой в полярных координатах имеет вид
r 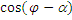 =p, (2.9)
=p, (2.9)
r,j,a,p – изображены на рисунке 25(полярная система координат).
4.2.1. Построить прямую, заданную уравнением 2x-y-4=0.
1). Для построения прямой достаточно знать координаты двух её произвольных точек. Полагая в уравнении прямой, например, x=0, получим y=-4. Имеем одну точку А(0;-4). Полагая x=1, получим y=-2. Отсюда вторая точка В(1;-2).Осталось построить точки А и В и провести через них прямую (рис. 26).
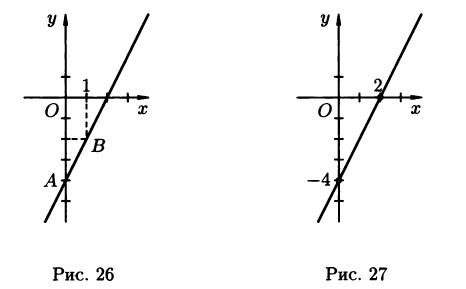
2). Задачу можно решить иначе, используя уравнение прямой в отрезках. Приведём уравнение к виду (2.3). Для этого перенесём свободный член (-4) в правую часть уравнения и обе его части разделим на 4. Получаем 2x-y=4,  -
-  = 1, т.е.,
= 1, т.е.,  -
- 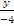 = 1 – уравнение прямой в отрезках на осях. На оси Оx отложим 2 единицы вправо (от начала координат); на оси Оy отложим 4 единицы вниз. Получаем две точки на осях,через которые проводим прямую (рис.27).
= 1 – уравнение прямой в отрезках на осях. На оси Оx отложим 2 единицы вправо (от начала координат); на оси Оy отложим 4 единицы вниз. Получаем две точки на осях,через которые проводим прямую (рис.27).
4.2.6.Уравнение прямой 4x-3y+12=0 представить в различных видах (с угловым коэффициентом, в отрезках, в виде нормального уравнения).
Для получения уравнения прямой с угловым коэффициентом разрешим заданное уравнение относительно y.Получим 3y=4x+12 b и далее y=  x+4 – уравнение прямой с угловым коэффициентом; здесь k=
x+4 – уравнение прямой с угловым коэффициентом; здесь k=  , b=4.
, b=4.
Для получения уравнения прямой в отрезках перенесём свободный член C=12 вправо и разделим обе части уравнения на -12. В результате получим, 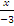 +
+  = 1- уравнение в отрезках на осях; здесь a=-3, b=4.
= 1- уравнение в отрезках на осях; здесь a=-3, b=4.
Приведём исходное уравнение к нормальному виду (2.8).
Для этого умножим обе части уравнения 4x-3y+12=0 на нормирующий множительl= 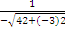 , т.е. l=
, т.е. l= 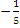 . Перед корнем взят знак «минус», т.к.свободный член (С=12) имеет знак «плюс». Получим -
. Перед корнем взят знак «минус», т.к.свободный член (С=12) имеет знак «плюс». Получим -  (4x-3y+12)=0, т.е. -
(4x-3y+12)=0, т.е. -  x+
x+  y-
y- 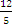 =0; здесь
=0; здесь  =
=  , sina=
, sina=  (
( 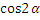 +
+ 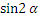 =
= 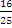 +
+ 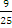 = 1), p=
= 1), p= 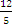 , т.е. расстояние от О(0;0) до прямой равно2,4.
, т.е. расстояние от О(0;0) до прямой равно2,4.
4.2.8. Написать уравнение прямой, проходящей через точки:
А) А(0;2), В(-3;7);
Б) А(2;1), В(4;1);
Решение:
А) Используем уравнение (2.6). Полагая в нём x1=0, y1=2, x2=-3, y2=7, получим 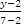 =
= 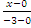 ,или
,или
 =
= 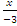 , т.е. -3y+6=5x или 5x+3y-6=0.
, т.е. -3y+6=5x или 5x+3y-6=0.
Б) Решаем аналогично: 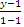 =
= 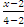 . Так как y1=y2, заключаем, что y-1=0, y=1 есть уравнение прямой, проходящей через точки А и В. (Для наглядности построим точки и прямую в системе Oxy- см.рис.28.)
. Так как y1=y2, заключаем, что y-1=0, y=1 есть уравнение прямой, проходящей через точки А и В. (Для наглядности построим точки и прямую в системе Oxy- см.рис.28.)
4.2.12 Из пучка прямых определяемых уравнением y+3=k(x-2) выделить ту, которая проходит через точку А(-2;5).
Подставим координаты точки А в уравнение прямой: 5+3=k(-2-2), получим k=8:(-4)=-2. Следовательно, искомое уравнение прямой есть y+3=-2(x-2), т.е. 2x+y-1=0.
4.2.14. Составить уравнение прямой в полярных координатах, если известно, что она проходит через точку М(2; t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>3</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 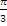 ) и наклонена к полярной оси под углом
) и наклонена к полярной оси под углом  p.
p.
Решение: воспользуемся уравнением(2.9). Очевидно(см.рис.29) a = 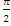 -(p -
-(p -  p)= t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
p)= t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>2</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  -
-  = t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>6</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
= t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>6</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  . Тогда
. Тогда
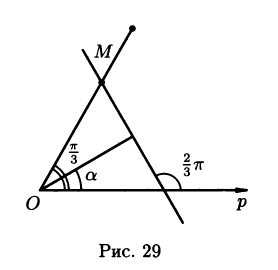
p=2 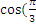 -
-  )=2
)=2 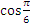 =2
=2 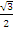 =
=  , т.е. p=
, т.е. p=  . Следовательно, уравнение искомой прямой есть r
. Следовательно, уравнение искомой прямой есть r  - t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>6</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
- t wx:val="Cambria Math"/><w:i/></w:rPr><m:t>6</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  )=
)= 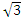 .
.