Функция (отображение, оператор, преобразование) - математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция - это "закон", по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Математическое понятие функции выражает интуитивное представление о том, как одна величина полностью определяет значение другой величины. Так значение переменной однозначно определяет значение выражения, а значение месяца однозначно определяет значение следующего за ним месяца, также любому человеку можно сопоставить другого человека - его отца. Аналогично, некоторый задуманный заранее алгоритм по варьируемым входным данным выдаёт определённые выходные данные.
Часто под термином "функция" понимается числовая функция; то есть функция которая ставит одни числа в соответствие другим. Эти функции удобно представляются на рисунках в виде графиков.
Табличный способ. Довольно распространенный, заключается в задании таблицы отдельных значений аргумента и соответствующих им значений функции. Такой способ задания функции применяется в том случае, когда область определения функции является дискретным конечным множеством.
При табличном способе задания функции можно приближенно вычислить не содержащиеся в таблице значения функции, соответствующие промежуточным значениям аргумента. Для этого используют способ интерполяции.
Преимущества табличного способа задания функции состоят в том, что он дает возможность определить те или другие конкретные значения сразу, без дополнительных измерений или вычислений. Однако, в некоторых случаях таблица определяет функцию не полностью, а лишь для некоторых значений аргумента и не дает наглядного изображения характера изменения функции в зависимости от изменения аргумента.
Графический способ. Графиком функции y = f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению.
Графический способ задания функции не всегда дает возможность точно определить численные значения аргумента. Однако он имеет большое преимущество перед другими способами - наглядность. В технике и физике часто пользуются графическим способом задания функции, причем график бывает единственно доступным для этого способом.
Чтобы графическое задание функции было вполне корректным с математической точки зрения, необходимо указывать точную геометрическую конструкцию графика, которая, чаще всего, задается уравнением. Это приводит к следующему способу задания функции.
Аналитический способ. Чаще всего закон, устанавливающий связь между аргументом и функцией, задается посредством формул. Такой способ задания функции называется аналитическим.
Этот способ дает возможность по каждому численному значению аргумента x найти соответствующее ему численное значение функции y точно или с некоторой точностью.
Если зависимость между x и y задана формулой, разрешенной относительно y, т.е. имеет вид y = f(x), то говорят, что функция от x задана в явном виде.
Если же значения x и y связаны некоторым уравнением вида F(x,y) = 0, т.е. формула не разрешена относительно y, что говорят, что функция y = f(x) задана неявно.
Функция может быть определена разными формулами на разных участках области своего задания.
Аналитический способ является самым распространенным способом задания функций. Компактность, лаконичность, возможность вычисления значения функции при произвольном значении аргумента из области определения, возможность применения к данной функции аппарата математического анализа - основные преимущества аналитического способа задания функции. К недостаткам можно отнести отсутствие наглядности, которое компенсируется возможностью построения графика и необходимость выполнения иногда очень громоздких вычислений.
Словесный способ. Этот способ состоит в том, что функциональная зависимость выражается словами.
Пример 1: функция E(x) - целая часть числа x. Вообще через E(x) = [x] обозначают наибольшее из целых чисел, которое не превышает x. Иными словами, если x = r + q, гдеr - целое число (может быть и отрицательным) и q принадлежит интервалу [0; 1), то [x] = r. Функция E(x) = [x] постоянна на промежутке [r; r+1) и на нем [x] = r.
Пример 2: функция y = {x} - дробная часть числа. Точнее y ={x} = x - [x], где [x] - целая часть числа x. Эта функция определена для всех x. Если x - произвольное число, то представив его в виде x = r + q (r = [x]), где r - целое число и q лежит в интервале [0; 1), получим {x} = r + q - r=q
Основными недостатками словесного способа задания функции являются невозможность вычисления значений функции при произвольном значении аргумента и отсутствие наглядности. Главное преимущество же заключается в возможности задания тех функций, которые не удается выразить аналитически.
9. Основные элементарные функции, их св-ва и графики, обратная функция.
Элементарные функции — функции, которые можно получить с помощью конечного числа арифметических действий и композиций из следующих основных элементарных функций:
алгебраические:,степенная;рациональная.,трансцендентные: показательная и логарифмическая;
тригонометрические и обратные тригонометрические.
Каждую элементарную функцию можно задать формулой, то есть набором конечного числа символов, соответствующих используемым операциям. Все элементарные функции непрерывны на своей области определения.
Иногда к основным элементарным функциям относят также гиперболические и обратные гиперболические функции, хотя они могут быть выражены через перечисленные выше основные элементарные функции.
Мы будем акцентировать внимание на следующем:
- область определения и значения функции;
- четность, нечетность функции;
- периодичность;
- монотонность;
- ограниченность;
- точки пересечения с осями координат;
- график функции.
Линейная функция y = kx + b.
la. Рассмотрим вначале частный случай функций y = kx + b при b = 0.
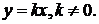
Функция определена при всех 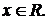
Областью значения является множество R (так как уравнение kx = c имеет решение при всех с).
Функция является нечетной, f(—x) = - kx = - f(x).
Функция не является периодической, так как k(x+T) = kx => kx + kT = kx => кТ = 0 => Т = 0.
Функция не ограничена.
Функция монотонная (при к > 0 возрастающая, k < 0 убывающая).
 |
Если у = 0, то х = 0.
1 б. Рассмотрим частный случай функции y = kx + b при k = 0.
у = b.
Эта функция определена при всех 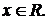
Областью значения является одна точка b.
Функция четная.
Функция периодическая (периодом является любое число, основного периода нет).
Функция ограничена.
Функция постоянная.
1 в. Функция y = kx + b.
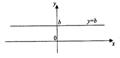
Функция y = kx + b является суммой двух функций y = kx и у = b. Следовательно область определения R (множество действительных чисел).
Область значения R.
Функция общего вида при 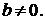
Функция не является периодической.
Функция не ограничена.
Функция монотонна (k > 0 возрастающая, k < 0 убывающая).
 |
График функции получается из графика функции y = kx сдвигом по оси ординат на величину b.
Дробно - линейная функция 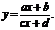
а, b, с, d - постоянные, причем 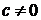 (иначе мы имели бы линейную функцию) и
(иначе мы имели бы линейную функцию) и  (иначе произошло бы сокращение и мы получили бы постоянную функцию).
(иначе произошло бы сокращение и мы получили бы постоянную функцию).
l a. В начале рассмотрим функцию 
Функция определена всюду, кроме х = 0, то есть область определения интервалы  .
.
Область значения также интервалы 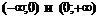 .
.
Функция нечетная, так как 
Функция убывающая (при к > 0) и возрастающая (при k < 0) на интервалах 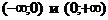 .
.
Функция неограниченная.
Полученная кривая называется гиперболой.
 |

1б. Общий случай 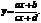
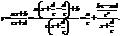
Полагая  получаем
получаем 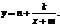
Следовательно график функции легко получить из графика функции 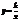 с помощью сдвига на - т вдоль оси Ох и на n единиц вдоль оси Оу.
с помощью сдвига на - т вдоль оси Ох и на n единиц вдоль оси Оу.
Свойства функции получаем из свойств функции 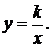
Квадратный трехчлен
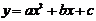 (
(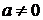 , иначе функция линейная).
, иначе функция линейная).
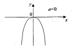
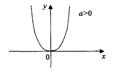
1а. Квадратная функция у=ах2.
Функция определена при всех х.
 Область значения неотрицательные числа (при a > 0) неположительные числа при а < 0.
Область значения неотрицательные числа (при a > 0) неположительные числа при а < 0.
- функция четная
- функция не является периодической
- функция ограничена снизу при а > 0, ограничена сверху при а < 0
- функция убывает на интервале ( ; 0) при a > 0
; 0) при a > 0
возрастает при a < 0
возрастает на интервале (0;  ) при а > 0
) при а > 0
убывает при а < 0.
1б. Общий случай 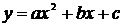 .
.
Получим: 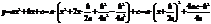 Полагая
Полагая 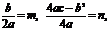 получим
получим 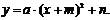
График данной функции получается из графика функции у = ах2
сдвигом на - т по оси Ох и сдвигом на п по оси Оу.
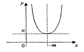
Степенная функция у = хn.
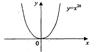
1а. Рассмотрим случай n = 2k.
Функция определена на всей числовой оси.
Функция четная, так как 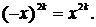
Функция не является периодической.
На интервале (- 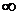 ; 0) функция убывает, на интервале (0; +
; 0) функция убывает, на интервале (0; + 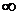 ) функция возрастает.
) функция возрастает.
Функция ограничена снизу.
 |
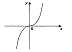
1б. Случай n = 2k + 1, y = x2к+1.
Функция определена всюду.
Функция нечетная.
Функция не является периодической. Возрастает на всей числовой оси.
Функция не ограничена.
Обратная функция
Пусть на некотором множестве Х задана функция у = f(x) и Y - область значения данной функции.
Возьмем некоторое число 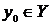 . Тогда найдется такое число
. Тогда найдется такое число 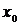 (возможно не единственное), что
(возможно не единственное), что 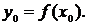 Таким образом, каждому значению
Таким образом, каждому значению 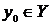 поставлено в соответствие число
поставлено в соответствие число 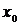 (возможно не единственное). Если такое число
(возможно не единственное). Если такое число 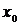 - единственное, то говорят, что задана функция х = g(y).
- единственное, то говорят, что задана функция х = g(y).
/Для существования обратной функции необходимо и достаточно, чтобы функция у = f(x) осуществляла взаимно-однозначное соответствие между множествами Х и Y./
Графики функции у = f(х) и обратной для нее функции х = g(y) совпадают, только аргумент обратной функции рассматривается на оси Оу.
Но если, следуя нашим привычкам, аргумент обозначить буквой х и откладывать его на оси Ох, то есть вместо х = g(y) писать у = g(x), то график функции у = g(x) отличается от графика функции у = f(х).
Легко показать, что графики функции у = f(x) и обратной к ней функции
у = g(x) симметричны относительно биссектрисы I и III координатных углов.
Заметим, что и свойства прямой, и обратной функций связаны между собой.
1. Область определения функции у = f(х) Х является областью значений функции 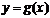 .
.
Область значения функции у = f(x) Y является областью определения функции 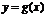 .
.
3. Если функция у =f(х) возрастает (убывает), то функция y = g(x) возрастает (убывает).
4. Если функция у = f(х) дифференцируема в точке 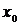 , то функция у = g(x) дифференцируема в точке
, то функция у = g(x) дифференцируема в точке 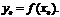
10. Элементарная функция, сложная функция.
Сложная функция - функция от функции. Если z - функция от у, т.е. z(y), а у, в свою очередь, - функция от х, т.е. у(х), то функция f(x) = z(y(x)) называется сложной функцией (или композицией, или суперпозицией функций) от х.
В такой функции х - независимая, а у - промежуточная переменная. При этом сложная функция определена для тех значений независимой переменной, для которых значения промежуточной функции у входят в область определения функции z(y).
Производная дифференцируемой сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточной функции по независимому аргументу:
.
Эта формула легко распространяется на случай, когда у сложной функции имеется два, три и более промежуточных аргументов ("цепное правило"): если z = f1(y1),y1 = f2(y2), …, yn-1 = fn(x), то

11. Определение числовой последовательности. Способы задания, арифметич.
прогрессиия и геометрич. прогрессия.
ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ - функция вида y = f(x), x? N,где N - множество натуральных чисел (или функция натурального аргумента), обозначается y = f(n) или y1, y2,…, yn,…. Значения y1, y2, y3,…называют соответственно первым, вторым, третьим, … членами последовательности.
Функцию y=f(x), x? N (Напомню, что N это натуральные числа, то есть числа от 1 до 9) называютфункцией натурального аргумента или же числовой последовательностью. Её обозначают следующим образом: y=f(n) или y1, y2, y3...,yn или (yn).
Ну а теперь давайте перейдём непосредственно к тем способам, которыми можно задать числовую последовательность.
Первый способ самый простой - словесный. Он используется, когда правило задания последовательности описано словами, не указывая формулы. Таким способом можно к примеру задать следующую последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,...
Второй способ - аналитический. Когда числовая последовательность задана формулой n-ного члена. Для наглядности я приведу три примера:
yn=n2 Это аналитическое задание последовательности чисел: 1, 4, 9, 16, 25...,n2,... Указав конкретное значение n, нетрудно найти член последовательности с соответствующим номером. К примеру нам нужно найти 10 член последовательности, значит n=10. Отсюда y10=102, а значит 10 член последовательности равен 100.
yn=C такая формула говорит нам о последовательности, которая имеет следующий вид: C, C, C, C,... такую последовательность называют постоянной или стационарной.
yn=2n это аналитическое задание последовательности 2, 22, 23, 24,...
3. Третий способ на мой взгляд самый интересный - это рекуррентный способ. Не пугайтесь этого слова, оно означает что нам даётся правило по которому можно вычислить следующие члены последовательности зная предыдущие. Заметьте, что именно правило а не формула, это очень важно! Далее я приведу три примера рекуррентного способа задания числовой последовательности.
Арифметическая прогрессия. Я уверен. что она знакома вам ещё с восьмого класса, она задана рекуррентно соотношениями: а1=а, аn+1=an+d (Где d - разность арифметической прогрессии, a и d - заданные числа)
Геометрическая прогрессия. Она вам тоже несомненно знакома, она рекуррентно задана соотношениями: b1=b, bn+1=bn*q (Где a и q - заданные числа, причём b?0 и q?0; q - знаменатель геометрической прогрессии).
Последовательность Фибоначи. Это возможно новое для вас понятие, но эта последовательность очень проста, каждый последующий её член равен сумме двух предыдущих. Она задана рекуррентно следующими соотношениями: b1=1, b2=1 bn=bn-2+bn-1Приведу начало этой последовательности для наглядности 1, 1, 2, 3, 5, 8, 13, 21...
Если каждому натуральному числу n (n = 1, 2,...) поставлено в соответствие число xn, то говорят, что задана числовая последовательность x1, x2,..., xn..., обозначаемая {xn}. Числаx1, x2,..., xn... называются членами последовательности, а член с номером n - ее n-м членом.
Арифметическая прогрессия
Числовую последовательность {an}, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом d, называют арифметической прогрессией. Число d называется разностью арифметической прогрессии: an+1 = an + d. Число Sn называется суммой n первых членов арифметической прогрессии.
Свойства арифметической прогрессии:

Геометрическая прогрессия
Числовую последовательность {bn}, первый член которой отличен от нуля, а каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q? 0, называют геометрической прогрессией.
Число q называется называется знаменателем прогрессии: bn+1 = bnq.
Число Sn называется суммой n первых членов геометрической прогрессии, Pn - произведением n первых членов геометрической прогрессии.
Свойства геометрической прогрессии:
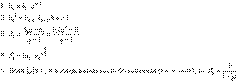
12. Определение предела ЧП.
Предел числовой последовательности - предел последовательности элементов числового пространства. Числовое пространство - это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому,
предел числовой последовательности - это такое число, что для всякой сколь угодно малой величины существует номер, начиная с которого уклонение членов последовательности от данной точки становится меньше заранее заданной величины.
Понятие предела последовательности вещественных чисел формулируется совсем просто, а в случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.
Предел (числовой последовательности) - одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений.[1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.
Определение. Число А называется пределом последовательности 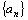 , если для любого положительного числа
, если для любого положительного числа  существует такой номер N, зависящий от
существует такой номер N, зависящий от  , что для всех номеров
, что для всех номеров  выполняется условие
выполняется условие  .
.
Обозначение: 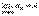 или
или  при
при 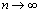 .
.
Определение. Последовательность, имеющая предел (из определения ясно, что A - конечно), называется сходящейся.
Определение. Если 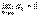 , то
, то 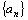 называется бесконечно малой последовательностью.
называется бесконечно малой последовательностью.
Определение. Последовательность 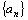 называется бесконечно большой, если для любого положительного числа M существует такой номер N, зависящий от M, что для всех номеров
называется бесконечно большой, если для любого положительного числа M существует такой номер N, зависящий от M, что для всех номеров 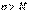 выполняется условие
выполняется условие 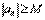 .
.
В этом случае говорят, что предел 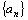 равен бесконечности и обозначают
равен бесконечности и обозначают  .
.
Определение. Последовательность, не являющаяся сходящейся, называется расходящейся.
Очевидно, что бесконечно большая последовательность является расходящейся.
13. Признак Бирштрасса, существование конечного предела ЧП.
Теорема Больцано - Вейерштрасса, или лемма Больцано - Вейерштрасса о предельной точке - предложение анализа, одна из формулировок которого гласит: из всякой ограниченной последовательности точек пространства 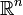 можно выделить сходящуюся подпоследовательность. Теорема Больцано - Вейерштрасса, в особенности случай числовой последовательности (
можно выделить сходящуюся подпоследовательность. Теорема Больцано - Вейерштрасса, в особенности случай числовой последовательности (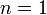 ), входит в каждый курс анализа. Она используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема носит имена чешского математика Больцано и немецкого математика Вейерштрасса, которые независимо друг от друга её сформулировали и доказали. В зависимости от признака, по к-рому производится выбор отрезковпри применении Б.-В. п. в., получается либо эффективный процесс, либо неэффективный. Примером первого случая является применение Б.-В. <п. в. к доказательству существования у непрерывной действительной функции, принимающей на концах нек-рого отрезка значения разного знака, точки на этом отрезке, в к-рой она обращается в нуль (см. Ноши теорема о промежуточных значениях непрерывной функции). В этом случае признаком, по к-рому производится последовательный выбор отрезков, является наличие у функции значений разных знаков на концах выбираемых отрезков. Если имеется способ вычисления функции в каждой точке, то в результате достаточно большого числа шагов можно получить координату точки, в к-рой функция на рассматриваемом отрезке обращается в нуль, с любой наперед заданной точностью. Таким образом, в этом случае одновременно с доказательством существования корня уравнения
), входит в каждый курс анализа. Она используется при доказательстве многих предложений анализа, например, теоремы о достижении непрерывной на отрезке функцией своих точных верхней и нижней граней. Теорема носит имена чешского математика Больцано и немецкого математика Вейерштрасса, которые независимо друг от друга её сформулировали и доказали. В зависимости от признака, по к-рому производится выбор отрезковпри применении Б.-В. п. в., получается либо эффективный процесс, либо неэффективный. Примером первого случая является применение Б.-В. <п. в. к доказательству существования у непрерывной действительной функции, принимающей на концах нек-рого отрезка значения разного знака, точки на этом отрезке, в к-рой она обращается в нуль (см. Ноши теорема о промежуточных значениях непрерывной функции). В этом случае признаком, по к-рому производится последовательный выбор отрезков, является наличие у функции значений разных знаков на концах выбираемых отрезков. Если имеется способ вычисления функции в каждой точке, то в результате достаточно большого числа шагов можно получить координату точки, в к-рой функция на рассматриваемом отрезке обращается в нуль, с любой наперед заданной точностью. Таким образом, в этом случае одновременно с доказательством существования корня уравнения 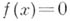 на отрезке, на концах к-рого функция принимает значения разных знаков, дается и метод приближенного решения этого уравнения. Примером второго случая является доказательство с помощью Б.-В. п. в. теоремы о достижимости действительной непрерывной на отрезке функцией ее верхней грани. Здесь при последовательном делении: отрезков пополам выбирается тот отрезок, на к-ром верхняя грань значений функции не меньше, чем на втором. Если, как и в первом случае, известен способ вычисления функции в каждой точке, то этого недостаточно для эффективного выбора нужного отрезка..Поэтому в этом случае с помощью В.- В. п. в. можно лишь доказать теорему существования, утверждающую, что рассматриваемая функция принимает в нек-рой точке свое наибольшее значение, а не получить метод для приближенного отыскания с наперед заданной точностью этой точки.
на отрезке, на концах к-рого функция принимает значения разных знаков, дается и метод приближенного решения этого уравнения. Примером второго случая является доказательство с помощью Б.-В. п. в. теоремы о достижимости действительной непрерывной на отрезке функцией ее верхней грани. Здесь при последовательном делении: отрезков пополам выбирается тот отрезок, на к-ром верхняя грань значений функции не меньше, чем на втором. Если, как и в первом случае, известен способ вычисления функции в каждой точке, то этого недостаточно для эффективного выбора нужного отрезка..Поэтому в этом случае с помощью В.- В. п. в. можно лишь доказать теорему существования, утверждающую, что рассматриваемая функция принимает в нек-рой точке свое наибольшее значение, а не получить метод для приближенного отыскания с наперед заданной точностью этой точки.
Имеются различные обобщения Б.-В. <п. <в., напр, на случай re-мерного евклидова пространства 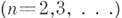 применительно к n-мерным кубам при последовательном их делении на конгруэнтные кубы с ребрами, вдвое меньшими ребер исходного куба. Л. Д. Кудрявцев.
применительно к n-мерным кубам при последовательном их делении на конгруэнтные кубы с ребрами, вдвое меньшими ребер исходного куба. Л. Д. Кудрявцев.
14. Определение предела функции на бесконечности.
Предел функции на бесконечности. Пусть задана функция у = f(x) с неограниченной сверху областью определения. Число b называется пределом данной функции при х, стремящемся к плюс бесконечности, если для любого числа существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x > M, выполняется неравенство |f(x) - b| <?. Запись этого факта: 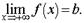
Если область определения данной функции неограниченна снизу, то число bназывается пределом данной функции при х, стремящемся к минус бесконечности, если для любого числа? < 0 существует такое положительное число М, что при всех значениях аргумента х из области определения, таких, что x < -M, выполняется неравенство |f(x) - b| <?. Записывается это так: 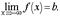
15. Определение предела функции в точке.
Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, - такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки - частный случай такой базы множеств.
Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе "стремление аргумента к бесконечности".
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказываетсянепрерывной (в данной точке).
Определения
Рассмотрим функцию 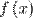 , определённую на некотором множестве
, определённую на некотором множестве 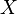 , которое имеет предельную точку
, которое имеет предельную точку 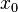 (которая, в свою очередь, не обязана ему принадлежать).
(которая, в свою очередь, не обязана ему принадлежать).
[править]Предел функции по Гейне
Значение 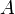 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции  в точке
в точке 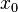 , если для любой последовательности точек
, если для любой последовательности точек  , сходящейся к
, сходящейся к 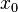 , но не содержащей
, но не содержащей 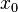 в качестве одного из своих элементов (то есть в проколотой окрестности
в качестве одного из своих элементов (то есть в проколотой окрестности 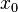 ), последовательность значений функции
), последовательность значений функции 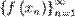 сходится к
сходится к 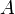 .[1]
.[1]
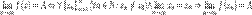
[править]Предел функции по Коши
Значение 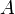 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции 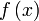 в точке
в точке 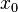 , если для любого наперёд взятого положительного числа
, если для любого наперёд взятого положительного числа  найдётся отвечающее ему положительное число
найдётся отвечающее ему положительное число 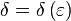 такое, что для всех аргументов
такое, что для всех аргументов 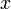 , удовлетворяющих условию
, удовлетворяющих условию 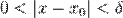 , выполняется неравенство
, выполняется неравенство 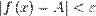 .[1]
.[1]
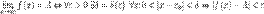
16. Односторонние пределы. Бесконечно большие и ограниченные пределы.
| Односторонние пределы |
Любой интервал (, а), правым концом которого является точка а, называется левой окрестностью точки а.
Аналогично любой интервал (a, ), левым концом которого является точка а, называется ее правой окрестностью.
Символически запись  означает, что х стремится к а справа, оставаясь большим а, то есть при х > а; означает, что х стремится к а справа, оставаясь большим а, то есть при х > а;  означает, что х стремится к а слева, то естьпри х < а. означает, что х стремится к а слева, то естьпри х < а.
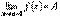 будем называть левосторонним пределом функции при будем называть левосторонним пределом функции при 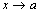 слева, слева, 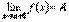 -это правосторонний предел функции.
Теорема. Функция у = f(х) имеет -это правосторонний предел функции.
Теорема. Функция у = f(х) имеет 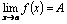  в том и только в том случае, когда существуют и равны друг другу ее в том и только в том случае, когда существуют и равны друг другу ее 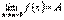 и и 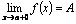 . Tогда . Tогда 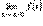 = = 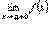 = = 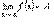
|
| Бесконечно малые и бесконечно большие |
Функция 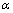 (х) называется бесконечно малой при ха, если (х) называется бесконечно малой при ха, если 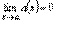 Ясно, что тогда (x) для x O (а, б) и > 0.
Функция f(х) называется бесконечно большой при Ясно, что тогда (x) для x O (а, б) и > 0.
Функция f(х) называется бесконечно большой при 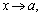 если если 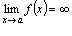 . Это равносильно тому, что каким бы ни было число М > 0, найдется такая окрестность О (а, б), что для всех x O (а, б) . Это равносильно тому, что каким бы ни было число М > 0, найдется такая окрестность О (а, б), что для всех x O (а, б) 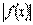 M.
Лемма. Если f(х) M.
Лемма. Если f(х)  при х при х  а, то а, то 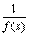  0 при ха. Если (x) 0 при x a, то 0 при ха. Если (x) 0 при x a, то 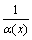 при x a и (x) 0.
Действительно, пусть f(x) , то есть является бесконечно большой. Тогда f(x) М для x O (а, б). при x a и (x) 0.
Действительно, пусть f(x) , то есть является бесконечно большой. Тогда f(x) М для x O (а, б). 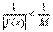 для x O (а, б), то есть для x O (а, б), то есть 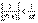 для x O (а, б), это означает, что для x O (а, б), это означает, что 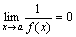 , так как , так как 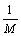 можно взять в качестве > 0. можно взять в качестве > 0.  Аналогично доказывается вторая часть утверждения.
Аналогично доказывается вторая часть утверждения.
|
17. Два определения БМВ(бесконечно малая величина).
Бесконечно малая (величина) - числовая функция или последовательность, которая стремится к нулю.
Бесконечно малая величина есть такая переменная величина, предел которой есть 0, или, что то же самое, это есть такая переменная величина, которая может быть сделана менее всякой данной величины. Поэтому Б. м. величину называют также иногда произвольно малою величиной.
1. Если переменная величина xn имеет своим пределом нуль lim xn = 0, то она называется бесконечно малой. Это же определение можно высказать и в другой формулировке:
Переменная величина xn назвается бесконечно малой, если для всякого наперед заданного положительного числа можно указать такое натуральное число N, что | xn | < для всех номеров n, которые больше N.
Ни одно число, кроме нуля, не может быть отнесено к бесконечно малым величинам.
2. Алгебраическая сумма нескольких бесконечно малых величин есть также величина бесконечно малая.
Алгебраической суммой называется такая сумма, члены которой присоединяются друг к другу не только при помощи знака плюс, но и при помощи знака минус.
3. Разность двух бесконечно малых величин есть величина бесконечно малая.
4. Произведение ограниченной переменной величины на бесконечно малую есть величина бесконечно малая.
Отсюда следует:
а) Произведение постоянной величины на бесконечно малую есть величина бесконечно малая.
б) Произведение переменной величины, стремящейся к пределу, на бесконечно малую есть величина бесконечно малая.
в) Произведение двух бесконечно малых величин есть величина бесконечно малая.
5. Отношение двух бесконечно малых величин не обязательно есть величина бесконечно малая.
Отношение двух бесконечно малых величин может быть величиной конечной, бесконечно малой и даже бесконечно большой величиной.
Об отношении двух бесконечно малых величин иногда говорят, что оно представляет собой "неопределенность" вида. 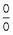
Вычисление предела отношения двух бесконечно малых часто называется также раскрытием "неопределенности" вида. 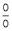
18. Связь между БМВ(бесконечно малая величина). и ББВ(бесконечно большая величина).
Бесконечно малые и бесконечно большие величины - Бесконечно малая величина есть такая переменная величина, предел которой есть 0, или, что то же самое, это есть такая переменная величина, которая может быть сделана менее всякой данной величины. Поэтому Б. м. величину называют также иногда произвольно малою величиной. Б. большая величина, или произвольно большая величина, напротив, есть такая, которая может быть сделана более всякой данной величины. Эти два вида переменных величин взаимно соответствуют один другому и должны быть рассматриваемы вместе. Так, в элементарной геометрии разность между длиной окружности круга и периметром вписанного или описанного многоугольника с произвольно большим числом сторон есть величина произвольно малая. Б. малые и Б. большие величины делят на различные порядки. Выбирая из данных переменных величин одну какую-нибудь за малую величину первого порядка, называют Б. малыми величинами того же первого порядка всякую Б. малую величину, отношение которой к данной есть величина конечная. Если же отношение это есть Б. малая величина и притом 1-го порядка, то ее называют Б. малой величиной 2 -го порядка и т. д. Таким образом, если, напр.,? есть бесконечно малая величина, а k какая-нибудь конечная ве