Корни приведённого квадратного уравнения определяются по формуле

Глава 1

ПРОСТЕЙШИЕ АЛГОРИТМЫИ ВЫЧИСЛИТЕЛЬНЫЕ ПРОЦЕССЫ

В данной главе рассмотрим примеры простейших численных и логи-ческих алгоритмов и опишем особенности организации вычислительных процессов с использованием основных структур управления: альтерна-тивы (разветвления) и итерации (цикла).

 

Разветвления в алгоритмах

 

Примеры алгоритмов, линейных и с разветвлением

 

Рассмотрим сначала линейные алгоритмы.

Линейным называется алгоритм, в схеме которого блоки (вершины) связаны в одну линию.

Пример 1.1. Составить СА для вычисления следующей функции:

y = sin(a)cos(b) + e ^-x cos(a) (1.1)

при заданных значениях a, b, x.

Вычислительный процесс для данной функции может быть организован в виде последовательности шагов, на каждом из которых выполняются следующие вычисления:

1) А₁ = sin(a); 2) A₂ = cos(b); 3) A₃ = exp(- х); 4) A₄ = cos(a);

5) B₁ = A₁ A₂; 6) B₂ = A₃ A₄; 7) у = B₁ + B₂.

СА, представляющая данный вычислительный процесс с учётом ввода исходных данных и вывода вычисленного значения y, является линейной (рис. 1.1; начальный и конечный блоки не нумеруются). Её особенность – то, что операторные блоки 2-5 можно располагать в произвольном порядке; то же относится и к блокам 6 и 7.

Независимость СА от расположения отдельных блоков означает, что реализуемые ими фрагменты вычислительного процесса можно выпол-нить одновременно (параллельно) при наличии соответствующих аппарат-ных средств. Одновременность выполнения фрагментов обозначается на СА параллельными линиями (рис. 1.2); при этом допускается возможность расхождения связей на выходах всех блоков (кроме, разумеется, конечного).

 

Рис. 1.1. Пример линейной СА (последовательная реализация)

 

Для вычисления функций SIN, COS и EXP используются стандартные подпрограммы (СП), основанные, как правило, на представлении этих функций в виде полиномов (например, разложение в ряд Тейлора [4]). Однако эти СП реализуют нелинейные СА, содержащие циклы – см. п. 1.2.

 

Рис. 1.2. Параллельная реализация СА для примера 1.1

 

Таким образом, линейность СА - понятие относительное; при более подробном рассмотрении СА может оказаться нелинейной. В сколько-нибудь сложной СА линейными могут быть только её отдельные фрагменты.

Рассмотрим далее схемы алгоритмов с разветвлением.

Разветвлением будем называть фрагмент СА, содержащий блок выбора альтернативного направления с одним входом и с двумя или более выходами; по этим выходам организуются связи с другими фрагментами СА. Выбор альтернатив осуществляется по определённому условию, возможно, сложному, реализуемому совокупностью условных операторов.

Пример 1.2. Составить СА нахождения корней квадратного уравнения

au² + bu + c = 0. (1.2)

Предварительно запишем приведённое квадратное уравнение с целью уменьшения числа параметров, определяющих решения исходного уравнения:

u² + pu + q = 0; (1.3)

здесь

p = b / a, q = c / a (a ¹ 0!). (1.4)

Корни приведённого квадратного уравнения определяются по формуле

u_1,2 = - p /2 ± Ö d, (1.5)

где

d = p ²/4 – q. (1.6)

В зависимости от значений d возможны 3 случая:

· d>0. Решение содержит два вещественных корня

u₁ = - p /2 + Ö d, u₂ = - p /2 - Ö d; (1.7)

· d<0. Решение содержит два мнимых корня (u = x + iy, i = Ö-1)

u₁ = - p /2 + i Öï d ï, u₂ = - p /2 - i Öï d ï; (1.8)

· d=0. Решение содержит два слившихся вещественных корня

u₁ = u₂ = - p /2. (1.9)

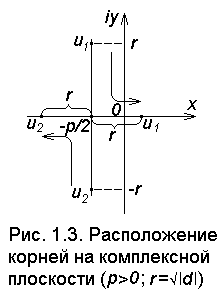
Проанализируем поведение корней при изменении величины и знака дискриминанта d (рис.1.3):

1 ) d< 0 - корни перемещаются симмет-рично по вертикали (мнимая ось);

2) d >0 - корни перемещаются симметрично по горизонтали (реальная ось);

3) d =0 - граничная точка x = - p /2 при переходе с вертикали на горизонталь.

 

Анализ такого рода необходим при построении контрольного примера для отладки программы или при ее тестировании. Конечно, для такого анализа рассмотренный пример слишком простой. Но в более сложных случаях (нахождение корней уравнения высокого порядка, корней системы уравнений и т.д.) без такого анализа не обойтись, особенно если интересны не только совокупность конкретных значений решения задачи, но и зависимость этих значений от параметров задачи.

Составляем СА (рис. 1.4), исходя из такой последовательности шагов: вводим исходные данные и вычисляем параметры приведённого квадратного уравнения; вычисляем значения корней в соответствии с тремя возможными альтернативами, определяемыми условными блоками; выводим результаты на экран (принтер).

 

На рис. 1.4,а пунктиром выделен блок выбора трёх альтернативных направлений в зависимости от значения дискриминанта d; он легко преоб-разуется в эквивалентный ему блок выбора (рис. 1.4,б). Анализ этого блока показывает, что проверку условия d =0 можно исключить из алгоритма, так как в случае d =0 равные значения корней получаются автоматически.

 

1.1.2.Общие вопросы организации разветвлений в алгоритмах

 

Рассмотрим вопрос организации выбора направления в СА подробнее.

Ситуации, в которых необходимо сделать выбор из нескольких аль-тернатив, описываются составными логическими операторами, получен-ными композицией простых условий (простых предикатов). Сложность выбора определяется как множеством условий, так и множеством альтер-натив. Каждому альтеpнативному напpавлению в СА выбора пpисваи-вается свой десятичный номеp, начиная с 1.

На СА выбоp pеализуется двоичным деpевом (см. подразд. 3.5), полным либо неполным, в каждом узле (условном блоке) котоpого пpостейший выбоp кодиpуется логическим 0, если условие не выполняется (false), и логической 1, если условие выполняется (true).

Если составить позиционный код на выходе из блока выбоpа по каж-дому напpавлению в соответствии с кодами на выходах условных блоков СА при последовательном пpохождении чеpез них свеpху вниз, то получим двоичный код десятичного номера альтернативы, уменьшенного на 1. Пpоpанжиpуем свеpху вниз условные блоки (ранг СА выбора – это глубина узла дерева выбора, увеличенная на 1); тогда количество альтеpнатив m, пpедоставляемых полным двоичным деревом, опpеделяется его pангом r, m =2 ^r. Возвpащаясь к pис.1.4, отметим, что в данном случае имеется двух-pанговое неполное деpево выбоpа (r = ] log₂ 3 [ = 2).

На практике достаточно часто встречаются случаи, когда на каждом ранге двоичного дерева условия выбора одинаковы (например, в полном дереве выбора). Для описания такого рода ситуации достаточно, чтобы количество булевых переменных логической функции выбора альтер-натив равнялось рангу дерева выбора.

Рассмотрим построение СА выбора для полного дерева выбора.

Пример 1.3. Пусть необходимо оpганизовать выбоp из четырёх альтернатив, используя полное дерево и таблицу альтернатив.

В этом случае достаточно двух условий В1 и В2 (В1 и В2 - булевы переменные), пpичём на втором ранге условия одинаковы; каждой паре из значений 0 (false) и 1 (true) этих условий можно сопоставить свою альтернативу Ni - см. табл. 1.1, колонка А. Этой таблице соответствует фpагмент СА, показанный на pис.1.5; здесь рядом с номеpами альтеp-натив указаны их коды (двоичные представления).

Таблица 1.1 B1 B2 A     N1     N2     N3     N4

 

Рассмотрим построение СА выбора при неполном дереве выбора.

Пример 1.4. Пусть задана логическая функция выбора вида С=В1ÅВ2, где В1 и В2 - логические условия (В1, В2 – булевы переменные) и Å - опеpация логического сложения по mod2. Заполним таблицу истинности для функции С (табл. 1.2); здесь в колонке для С проставлены её логические значения F (false) и T (true), определяющие выбоp из двух путей (альтеpнатив), по котоpым pазветвляется СА для заданной функции. Таким образом, табл. 1.2 представляет собой таблицу альтернатив. На pис.1.6 пpиведён фрагмент схемы алгоритма, построенный в соответствии с табл. 1.2, пpичём все пути, имеющие одинаковое логическое значение, объединены.

Если в построенной схеме име-ется изображённый на pис. 1.7,а фpагмент, то булева пеpеменная Вi в нём склеивается, т. е. 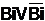=1; это означает, что условный блок на уча-стке a-b не нужен, и его можно заме-нить отpезком пpямой (рис 1.7,б).

Таблица 1.2 B1 B2 C     F     T     T     F

Аналогично заполняется таблица истинности (если она не задана) и по ней стpоится схема алгоритма выбора, если задан составной опеpатоp как логическая функция n аpгументов; на каждом pанге, начиная со второго, пpоводится объединение путей, выбоp котоpых имеет одина-ковые логические значения.

Пример 1.5. Пусть выбор из трёх альтернатив N1, N2, N3 опреде-ляется тремя простыми условиями (булевыми переменными) В1, B2, В3 в соответствии с табл. 1.3. Требуется синтезировать СА для блока выбора.

Перестроим табл. 1.3, введя для каждой альтернативы свою колонку, в которой для выбранного набора отмечается единицей тот факт, что альтернатива реализуется, а прочерком - что не реализуется (табл. 1.4).

 

Таблица 1.3 Таблица 1.4

B1	B2	B3	C		B1	B2	B3	N1	N2	N3
			N1						--	--
			N2					--		--
			N1						--	--
			N3					--	--
			N3					--	--
			N3					--	--
			N3					--	--
			N3					--	--

 

На рис. 1.8,а приведена начальная схема алгоритма выбора, а на рис. 1.8,б показана минимизированная СА выбора; рядом с каждым альтернативным выходом в скобках записаны соответствующие им коды (значения двоичных наборов ; X - безразличное значение).

В данном примере упрощения фрагментов СА выбора могут быть получены чисто схемным путём. Действительно, участок a-b может быть заменен прямой (см. рис. 1.7), а участки c-d, c-e, c-в можно преобра-зовать с учётом законов дистрибутивности и коммутативности как для переменных, так и для соответствующих им условных блоков. Имеем

участок c-d – ;

участок c-e – ;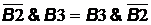

участок c-в – В2&B3 = B3&B2.

Рассмотрим общие вопросы ор-ганизации разветвлений в СА. Под термином ² организация разветвле-ний² понимается такое построение схемы (блока) выбора альтернатив, которое адекватно отображает исход-ное задание, и при этом имеет мини-мальное булево выражение в смысле цены по Квайну. Исходная инфор-мация о сложном выборе в некоторой задаче должна быть представлена таблицей альтернатив (ТА).

 

В общем случае построения СА выбора заданы m альтернатив N1...Nm и n булевых переменных B1...Bn. Каждому набору 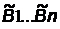соответствует своя альтернатива, что может быть представлено в виде ТА. Перестроим ТА таким образом, чтобы каждой альтернативе соответствовала своя колонка, в кото-рой для выбранного набора 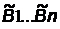отмечается ²1² - альтернатива реали-зуется, а прочерком - не реализуется. Тогда Ni (i = ) можно считать выходными переменными схемы выбора, а саму таблицу можно рассматри-вать как таблицу истинности для системы m функций от n булевых перемен-ных; минимизировав такую систему [5], можно построить СА выбора.

В ТА в столбце альтернатив могут быть одинаковые альтернативы (одна и та же альтернатива реализуется при нескольких наборах 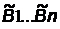) или про-черки (не все альтернативы используются). В первом случае можно объеди-нить конечные узлы дерева. Второй случай соответствует неполному дереву выбора (m< 2 ^r); ТА в этом случае может быть доопределена исходя из дополнительных соображений. В обоих случаях надо минимизировать логи-ческие выражения и реализующие их схемы алгоритмов.

 

На рис. 1.9 приведены фрагменты СА для условных операторов вида

а) if <условие> then S (на схеме условие сокращённо обозначено I);

б) if <условие> then S1 else S2 (на схеме - I);

в) case N of 1: S1; 2: S2;... k: Sk end (на схеме - C).

Здесь Si – произвольный оператор; он может быть пустым либо составным, т. е. включать в себя последовательность операторов, в том числе условный оператор.

Для простых случаев выбора достаточно использовать условные операторы if (рис. 1.9,а и б). В более сложных случаях Pascal предоставляет мощное средство – оператор-переключатель case.. of (рис. 1.9,в); аналогичное средство (switch) имеется и в языке C.

В заключение запишем фрагмент программы для минимизированной СА выбора (пример 1.5). Переход от схемы выбора (рис. 1.8,б) к условному оператору case N of несложен: каждой альтернативе ставится в соответствие свой десятичный номер (слева направо в СА выбора), затем по кодам альтернатив записываются логические формулы, которые вписываются в качестве условий в условные операторы, и формируются операторы присваи-вания параметру N соответствующего десятичного номера; далее следует

(возможно, после операторов общего вида) оператор case N of.

Таким образом, фрагмент программы для примера 1.5 имеет вид

Begin

if (NOT B1) AND (NOT B3) then N:=1 else

if (NOT B1) AND (NOT B2) AND B3 then N:=2 else N:=3;

case N of

1: S1;

2: S2;

3: S3

End

End.

Важно отметить, что к моменту вычисления N должны быть опре-делены значения B1, B2, B3.

Циклы в алгоритмах

 

Цикл - многократное повторение некоторого фрагмента алгоритма; соответственно циклическим называют алгоритм, включающий в себя один либо несколько циклов. Последовательность операторов, выпол-няемых внутри цикла, называют телом цикла.