1. Возрастание и убывание функции.
Функция f(x) называется возрастающей ( убывающей ) в интервале (а;b), если каковы бы ни были значения х1 и х2 из этого интервала, из неравенства х2>х1 вытекает неравенство f(х2)>f(х1) (f(х2)<f(х1)).Если же для таких х1 и х2 из неравенства х2>х1Þ f(х2)³f(х1) (f(х2)£f(х1)), то функция f(x) называется неубывающей (невозрастающей) на (а;b).
Функции всех этим типов носят общее название – монотонные.
Монотонные функции часто встречаются в различных исследованиях. Высота растущего дерева, например, или вес созревающего зерна – это монотонные неубывающие функции времени; освещенность, меняющаяся по мере удаления от источника света – монотонно убывающая функция расстояния. Существуют и не монотонные функции. Например, tо воздуха в течение года – не монотонная функция времени, хотя на протяжении нескольких часов она может быть и монотонной, повышаясь к полудню или понижаясь к вечеру.
Теорема 1 (необходимое условие монотонности). Если функция у=f(x) дифференцируемая в интервале (а;b), не убывает (не возрастает) на нем, то ее производная в этом интервале неотрицательна (неположительна), т.е. f¢(x)³0 (f¢(x)£0).
Доказательство.
Пусть х- произвольное значение из интервала (а;b). Придадим этому значению х приращение Dх такое, чтобы точка х+Dх принадлежала интервалу (а;b). Если f(x) – неубывающая функция, то Dу³0 при Dх>0 и Dу£0 при Dх<0. В обоих случаях  ³ 0 и Þ
³ 0 и Þ 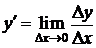 ³ 0.
³ 0.
Если же f(x) – невозрастающая функция, то  £0 и f¢(x)£0.
£0 и f¢(x)£0.
Теорема 2 (достаточное условие монотонности). Если функция f(x), дифференцируемая в интервале (а;b) удовлетворяет в нем условию f¢(x)> 0 (f¢(x)<0), то эта функция возрастает (убывает) в интервале (а;b).
Пример 1. Функция  всюду возрастает, т.к.
всюду возрастает, т.к.  >0 "х.
>0 "х.
Пример 2. Функция у=х2 убывает в промежутке (-¥; 0). Т.к. в этом промежутке у¢=2х<0. Эта же функция в промежутке (0; +¥) возрастает, т.к. у¢=2х>0.
Учитывая определения убывающей и возрастающей на интервале функции, можно записать, что функция убывает на промежутке (-¥; 0] и возрастает на [0;+ ¥).
2. Максимумы и минимумы функции.
Функция f(x) имеет в т.х0 максимум (минимум), если существует такая окрестность точки х0 (х0-d; х0+d), что для всех х из этой окрестности, отличных от х0, выполняется неравенство: f(x)<f(х0) (f(x)>f(х0)). Иначе говоря, функция f(x) имеет в т. х0 максимум (минимум), если для достаточно малого приращения Dх (любого знака) выполняется неравенство: f(x0+Dх)<f(х0) (f(x0+Dх)>f(х0)).
Максимум и минимумфункции называют экстремумами функции.
По определению максимума и минимума функции они могут достигаться лишь внутри области определения, концы сегментов области определяются не могут служить точками, в которых функция принимает экстремум.
Если исследуемая на экстремум функция дифференцируема, то изучение свойств ее производной дает возможность находить точки, в которых функция принимает экстремум.
Теорема 1 (необходимое условие существования экстремума). Если функция f(x), дифференцируемая в интервале (а;b), имеет в точке х0, а<х0<b, экстремум, то её производная в этой точке равна 0: f¢(x)=0.
Теорема 2 (достаточное условие существования экстремума). Если производная функции f(x) обращается в точке х0 в 0 (такие точки называют критическими) и при переходе через эту точку в направлении возрастания х меняет знак + (-) на – (+), то в точке х0 эта функция имеет максимум (минимум). Если же при переходе через точку х0 производная функции f(x) не меняет знака, то в этой точке функция f(x) экстремума не имеет.
Отсюда следует такое правило исследования функции на экстремум с помощью 1-ой производной. Пусть в интервале (а;b) дана дифференцируемая функция f(x):
1) находим её производную f¢(x);
2) находим корни уравнения f¢(x)=0;
3) определяем знак f¢(x) слева и справа от каждого из этих корней и согласно Т.2 выносим заключение об экстремуме;
4) выясняем значение функции в точках экстремума.
 Пример 1. Исследовать функцию f(x)=ех–х на экстремум.
Пример 1. Исследовать функцию f(x)=ех–х на экстремум.
 Область определения D(f)=R.
Область определения D(f)=R.
f¢(x)=ех–1, ех–1=0, ех=1,
х=0 – критическая точка.
На интервале (-¥; 0] функция убывает, на интервале [0; +¥) функция возрастает. Точка х=0 – точка минимума, minf(x)=f(0)=e0=1.
Пример 2. Исследовать функцию f(x)=х3–3х+2 на экстремум.
Область определения D(f)=R.
 f¢(x)=3х2–3, 3х2–3=0, х=±1 – критические точки.
f¢(x)=3х2–3, 3х2–3=0, х=±1 – критические точки.
На интервалах (-¥;-1]È[1;+¥) функция возрастает, на интервале [-1;1] функция убывает. Точка х=-1 – точка минимума, точка х=1- точка максимума, minf(x)=f(-1)=4, maxf(x)=f(1)=0.