Правила дифференцирования

Таблица производных простейших функций

№	Функция	Производная	Частные случаи
	x a	a x a-1	1' = 0; x ' = 1; (х 2)' = 2 x; ;
	ах	ах × lna	(amx)' = m × amx × lna; (еmx)' = m × emx.
	logax
	sinx	cosx	(sin(mx))¢ = m× cos(mx).
	cosx	- sinx	(cos(mx))¢ = - m× sin(mx).
	tgx		(tg(mx))¢ = .
	ctgx		(ctg(mx))¢ = .
	arcsinx		(arcsin(mx))¢ =
	arccosx		(arcos(mx))¢ = -
	arctgx		(arctg(mx))¢ =
	arcctgx		(arcctg(mx))¢ =

 

Доказательства этих формул и следующих правил предлагается читателю рассмотреть самостоятельно [8, с. 54].

Правила дифференцирования

1. Производная постоянной функции равна нулю: с ' = 0.

2. Постоянный множитель можно выносить: (с × u)' = c × u '. 3. Производная суммы равна сумме производных: (u + v)' = u ' + v '.

4. Производная произведения: (u × v)' = u '× v + u × v '.

Пример 2. Найти производные следующих функций.

1). y = 2 х ³ -5 x ² + 7 x + 4.

Последовательно применяются правила дифференцирования 3, 2, 1 и формула 1 из таблицы производных: у ' = (2 х ³)' - (5 x ²)' + (7 x)' + (4)' =

2× (х ³)'- 5×(x ²)' + 7×(x)' + 0 = 2×3 х ² - 5×2 x ¹ + 7×1 = 6 х ² - 10 x + 7.

2). у = х ²× е ^х.

Применяются правило 4 и формулы 1, 2 из таблицы производных:

у ' = (х ²)'× е ^х + х ²×(е ^х)' = 2 х ¹× е ^х + х ²× е ^х = х × е ^х (2+ х).

3). у = хÖ ` x ×(lnx -2).

Выражение хÖ ` x переписывается как , тогда у = ×(lnx - 2). Применяются правило 4 и формулы 1, 3 из таблицы производных:

у ' = (х ^3/2)'×(lnx - 2) + х ^3/2× (lnx - 2)' = (3/2)×(х ^1/2)×(lnx - 2) + х ^3/2×(l/ x - 0) = 1,5 Ö ` x<sup>.</sup>lnx -2 Ö ` x.

 

Следующее правило применяется при вычислении производной сложной функции.

Пусть F (x)= (f * g)(x) = f (g (x)) - суперпозиция двух функций f (u) и g (x). При этом f (u) - внешняя функция, g (x) - внутренняя функция, буква u - промежуточный аргумент. И пусть существуют: g_x'(x ₀) - производная внутренней функции в точке x ₀ и f_u '(u ₀) - производная внешней функции точке u ₀ = g (x ₀). Тогда существует F '(x ₀) - производная сложной функции F (x) в точке x ₀ и выполняется равенство:

 

F '(x ₀) = f_u '(u ₀) × g _x '(x ₀). (44)

 

Другими словами, производная сложной функции равна произведению прозводной внешней функции по промежуточному аргументу на производную внутренней функции.

Пример 3. Вычислить производные следующих функций.

1). y = log ₃ (5 x ²+3).

Здесь log ₃ (5 x ²+3) - сложная функция: u = (5 x ²+3) - внутренняя и у =

log ₃ u - внешняя функции. По формуле 3, (log ₃ u)' = 1/ (u × ln 3), а (5 x ²+3)¢ =

= (10 x +0) = 10 x. Тогда, по формуле (44),

Здесь u = 1 – х ² - внутренняя функция и у = Ö ` u - внешняя функция.

Тогда и u¢ = (1 - x ²)¢ = -2 x. Следовательно,

Здесь u = - x ² - внутренняя и у = e^u - внешняя функции. Тогда (e^u)' = e^u, и (- x ²)¢ = -2 x. Следовательно, по формуле (44),
y ¢= e^u ×(-2 x) = -2 x .

4). y = x ⁴× (8× ln ² x - 4× lnx + 1).

По правилу 3, y '= (x ⁴)'×(8× ln ² x - 4 lnx + 1) + x ⁴×(8× ln ² x - 4× lnx + 1)' = 4 x ³×(8× ln ² x - 4× lnx + 1) + x ⁴×(8×2× lnx ×(1/ x)- 4×(1/ x)+ 0) = 32× x ³× ln ² x.

Из свойств логарифмов следует: y = (2/3)(ln (1-3 x) - ln (1+3 x)).

 

В следующем примере применяется так называемый метод логарифмического дифференцирования. Если исходная функция y = f(x) получена с помощью операций умножения, деления, возведения в степень или извлечения корня, то сначала находят логарифм этой функции: lny = lnf(x), при этом правую часть преобразуют с помощью соответствующих свойств логарифмов. Затем находят производные от обеих частей полученного равенства, при этом считают, что (ln y)¢= . Из вновь полученного равенства выделяют искомую производную у ¢.

Сначала логарифмируют обе части исходного равенства:

Теперь, дифференцируют это равенство:

Производная у ¢ = f¢ (x) называется производной 1-го порядка. И ее можно рассматривать как функцию от х. Тогда производная от f¢ (x) называется производной 2-го порядка и обозначается через у ¢¢= f ¢¢(x). Это понятие распространяется на все натуральные числа следующим образом.

Определение 2. Производной n - го порядка от функции f (x) по х называется производная по х от ее производной (n- 1)-го порядка, (обозначение:

y ^{( n )}= f ^{( n )}(x)).

Пример 4. Найти производные второго и третьего порядков.

1). y = x× lnx.

Решение. Сначала находится производная 1-го порядка: y ¢ = x ¢ × lnx +

х× lnx ¢ = 1 × lnx + x× 1/ х = lnx + 1. От полученной функции снова берется производная: y ¢¢ = lnx ¢+ 1¢=1/ х + 0 = 1/ х. Аналогично, y ⁽³⁾ = (1/ х)¢= -1/ х ².

2). y = x ³ × e^x .

Решение. у ¢ = х ³¢ × е^х + х ³ × е^х ¢=3 х ² × е^х + х ³ × е^х ¢= е^х× (3 х ² + х ³) ; у ¢¢ =

e^x ¢ × (3 x ²+ x ³) + e^x× (3 x ²+ x ³) ¢= e^x× (3 x ²+ x ³) + e^x× (6 x +3 x ²) = e^x× (6 x ²+ x ³ + 6 x);

у ⁽³⁾ = е^х ¢ × (6 х ²+ х ³ + 6 х) + е^х× (6 х ²+ х ³+ 6 х)¢ = е^х× (9 х ²+ х ³ +18 х + 6).

 

§2. Задачи, приводящие к понятию производной функции

 

Залача о мгновенной скорости движения. Пусть точка М движется вдоль числовой оси ОХ и в каждый момент времени t ее координата равна s (t). Тогда равенство s = s (t) называется уравнением движения точки М. Пусть рассматривается момент t _o, и t - некоторый другой момент, (см. чертеж 33). В момент t _о точка М имеет координату s (t _о) и в момент t - координату s (t). Тогда разность D s = s (t) - s (t _о) есть расстояние, пройденное точкой М за время D t = (t - t _o), а отношение = есть средняя скорость движения.

 

D s

0 s(t ₀ ) s(t) X

Черт.33.

Но более правильное представление о скорости движения в момент t ₀ дает предел этого отношения, когда t стремится к t _o, и этот предел называется мгновенной скорстью движения точки М:

Ясно, что этот предел является производной функции s (t) в точке t _o. Получен следующий физический смысл производной: если функция s (t) задает уравнение движения точки, то производная s ¢(t _o ) есть мгновенная скорость движения точки в момент t _o.

Аналогично показывается, что производная второго порядка s ²(t _o)есть мгновенное ускорение движения точки в момент t _o,.

Пример 5. Пусть S = t ³ – 6 t ² + t - расcтояние в метрах, пройденное телом в течение t секунд. Определить скорость и ускорение при t = 3 c.

Решение. Скорость v в момент t равна производной S ¢= 3 t ² - 12 t + 1, тогда при t = 3 скорость равна v = 3×3² - 12×3 + 1= -8 м/с. Ускорение w в момент t есть производная от скорости: w = v ¢ = 6 t - 12. При t = 3 ускорение равно w = 6×3 - 12 = 6 м/с².

Теперь, рассматриваются примеры применения понятия производной в экономике.

Задача о предельных издержках производства. Пусть х обозначает количество выпускаемой продукции и у - издержки производства. Тогда у считается функцией от количества выпускаемой продукции: у = f (x). Пусть в некоторые моменты времени выпуски продукции составили х _о и х (ед.), а издержки производства равны f (x _o) и f (x) (ден. ед.), соответственно. Тогда D х = х - х _о есть прирост продукции, D у = f (x) - f (x _o) - приращение издержек производства, и отношение = 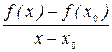называется средним приращением издержек производства на единицу продукции. Но для характеристики скорости изменения денежных затрат вводятся так называемые предельные издержки производства, которые равны производной этой функции:

Аналогично с помощью производной могут быть определены предельная выручка, предельная себестоимость и другие предельные величины. При этом средние величины характеризуют состояние соответствующего экономического объекта, а предельные величины характеризуют скорость изменение этого объекта. Таким образом, производная выступает как скорость изменения некоторого экономического процесса. Однако, следует учесть, что экономика и другие социальные науки не всегда позволяют использовать предельные величины в силу неделимости многих экономических объектов и в силу прерывности экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). Вместе с тем в ряде случаев оказывается возможным отвлечься от дискретности этих показателей и эффективно использовать предельные величины.

Задача о темпе производственной функции. Пусть функция у = f (t) описывает некоторый производственный показатель. Тогда рассматривается относительная скорость изменения этой функции, которая называется темпом данного показателяи определяется как логарифмическая производная:

Например, рассматривают темпы роста производительности труда, темпы изменения себестоимости продукции.

Задача об эластичности функции. Эластичностью функции у = f (x) называется предел отношения относительного приращения функции к относительному приращению аргумента х при D х ® 0:

Коэффициент эластичности Е_х (y) показывает приближенно, на сколько процентов изменится функция y при изменении аргумента х на 1%. Например, если y – спрос на некоторый товар и х – цена товара, то Е_х (y) показывает на сколько процентов изменится спрос при изменении цены на 1%. Если |Е_х (y)| > 1, то спрос считают эластичным, если |Е_х (y)| = 1, то – нейтральным, если |Е_х (y)| < 1, то спрос неэластичен относительно цены.

Задача о касательной. Рассматривается график функции у = f (x) и точка М _о(х _о; у _о) на этом графике. Требуется определить касательную к графику в точке М _о и найти ее уравнение. Так как М _о лежит на графике, то ее координаты удовлетворяют уравнению графика, т.е. выполняется равенство: у _о = f (x _o). Пусть М (х; у) – произвольная точка на графике, тогда ее координаты удовлетворяют равенству: у = f (x). Пусть эти точки проецируются на оси координат (см. чертеж 34), и M _о N параллельна оси ОХ.

 

Y

 

y M

D y

у = f (x) K

y ₀ M ₀ dy

D x N

a X

0 x ₀ х

Черт.34.

В треугольнике МNM _o: M _о N = (х - х _о) = D х, NM = (у - у _о) = D у, отношение NM к M _о N равно тангенсу угла NM _о M: = tg (Ð NM _о M). Касательной к графику функции f (x) в точке М _о называется прямая линия, к которой стремятся хорды М _о М, когда точка М стремится к точке М _о по графику.

Если точка М будет двигаться по графику к точке М _о, то х будет приближаться к х _о, и отношение будет стремиться к tg a, где a - угол наклона касательной к оси ОХ. Величина tg a называется угловым коэффициентом касательной. С другой стороны, предел отношения при х ® х _о равен производной функции f (x) в точке х _о. Получен следующий геометрический смысл производной:

производная функции f (x) в точке х _о равна угловому коэффициенту касательной к графику этой функции в точке М _о(х _о; f (x _о)): f ¢(x _o) = tg a.

Теперь, применяется уравнение (20) из главы 2 и получается следующее уравнение касательной к графику f (x) в точке М _о:

у = f ¢(x _o)(х - x _o) + f (x _o). (45)

Пример 6. Найти уравнения касательных к параболе у = 0,4 х ² - 3,2 х + 7,8 в точках пересечения ее с прямой у = 0,4 х + 2,2.

Решение. Координаты точки пересечения линий удовлетворяют обоим уравнениям, тогда эти координаты являются решениями системы: у = 0,4 х + 2,2,

у = 0,4 х ² -3,2 х + 7,8.

Здесь два решения: х ₁ = 7, у ₁ = 5 и х ₂ = 2, у ₂ = 3. Следовательно, получены две точки пересечения А (7; 5) и В (2; 3). Абсцисса вершины параболы С находится из уравнения у ¢(x) = 0, т.е. 0,8 x - 3,2 = 0, отсюда получается x = 4. Это подставляется в уравнение параболы: y = 1,4; тогда C (4; 1,4) - вершина параболы (см. чертеж 35).

 

y y = 0,4 x ² - 3,2 x + 7,8

 

A

y =0,4 x +2,2

B

 

С y =2,4 x -11,8

y =-1,6 x +6,2

M ₁ 0 M ₂ x

Черт.35.

 

Далее, применяется уравнение (45). Находится производная: у ¢ = (0,4 х ² -3,2 х + 7,8)' = 0,8 х -3,2. Значения у ¢ в точках х ₁ = 7 и х ₂ = 2 являются угловыми коэффициентами касательных в точках А и В: k ₁ = 0,8×7-3,2 = 2,4 и k ₂ = 0,8×2 -3,2 = -1,6. Эти значения подставляются в (45).

1) у = 2,4(х -7) + 5 «у = 2,4 х -11,8 - уравнение касательной в точке

А (7; 5).

2) у = -1,6(х -2) + 3 «у = -1,6 х + 6,2 - уравнение касательной в точке В (2; 3).

Для построения 1-й касательной берется A (7; 5) и новая точка М ₁(5; 0,2). 2-й касательная проходит через В (2; 3) и М ₂(4; -0,2).

 

Дифференциал функции

Пусть функция y = f (x) имеет конечную производную в точке х ₀ :

a ® 0 при D х ® 0; отсюда D y = f ¢(x ₀)×D х + a×D х. Величина f ¢(x ₀)×D х называется дифференциалом функции f (x), соответствующим точке x ₀ и приращению аргумента D х; обозначения: dy, df.

В частности, дифференциал функции y = x равен D х, т.е. dх = D х. Поэтому вместо D х пишут dх, тогда

dy = f ¢(x ₀)× dх. (46)

На чертеже 34 дифференциал dy равен отрезку NK, и потому говорят, что dy есть приращение касательной. Если f ¢(x ₀) ¹ 0, то dy является главной частью приращения функции D y. Поэтому можно считать, что при достаточно малом D х приращение функции D y = f (x) – f (x ₀) приближенно равно ее дифференциалу: D y » dy. Отсюда получается формула для приближенного вычисления значений функции:

 

f (x) » f (x ₀) + f ¢(x ₀)× dх. (47)

Пример 7. Для функции y = x ³ – 2 x +1 найти ее приращение D y и дифференциал dy, соответствующие точке x ₀ = 1 и приращению D х = 0,1.

Решение. Здесь x ₀ = 1, D х = dх = x – x ₀ = 0,1, поэтому х = 1 + 0,1 = 1,1.

Тогда f (x) = f (1,1) = 1,1³ – 2^. 1,1 +1 = 0,131; f (x ₀) = f (1) = 1³ – 2^. 1 +1 = 0, 1;

f ¢(x) = 3 x ² – 2; f ¢(x ₀) = f ¢(1) = 3^. 1² – 2 = 1. Получается: D y = f (x) – f (x ₀) = 0,131– 0= 0,131; dy = f ¢(x ₀)× dх = 1×0,1 = 0,1. Тогда D y и dy отличаются на 0,031, т.е. это отличие незначительное.

Пример 8. Вычислить приближенно Ö `34 помощью дифференциала.

Решение. Рассматривается функция y = Ö ` x, и пусть x <sub>0</sub> = 36, х = 34. Тогда D х = 34 –36 = - 2; f (x) = Ö `34; f (x ₀) = Ö `36 = 6; f ¢(x) = (Ö ` x)¢ = 1/(2 Ö ` x); f ¢(x <sub>0</sub>) = 1/(2 Ö `36) = 1/12. Теперь, применяется формула (47): Ö `34 » 6 + (1/12)×(-2) = 1 = 6 - 1/6 » 5,833. Легко видеть, что полученное значение 5,833 отличается от истинного значения Ö `34 не более чем на 0,002, т. е. формула (47) дает достаточно точные значения функции.