Определители 2-го и 3-го порядков.
В алгебре и аналитической геометрии широко используются алгебраические выражения специального вида, которые называются определителями. Определители составляются из элементов квадратных таблиц – матриц.
Определители 2-го порядка.
Матрицей второго порядка называется квадратная таблица из 4-х элементов, расположенных в виде двух строк и двух столбцов:
Строки матрицы нумеруются сверху вниз, столбцы – слева направо. Если элементы матрицы – числа, то матрица называется числовой матрицей. Определителем (детерминантом) второго порядка, соответствующим данной матрице, называется выражение
| Схема образования определителя второго порядка |
Левая часть последнего равенства представляет собой обозначение определителя второго порядка.
Определитель второго порядка не изменится, если сделать его строки столбцами, записав их в том же порядке:
.
Определители 3-го порядка.
Матрицей третьего порядка называется квадратная таблица из 9 элементов, расположенных в виде трех строк и трех столбцов.
Диагональ матрицы, на которой стоят элементы 
, 
, 
называется ее главной диагональю.
Определителем (детерминантом) третьего порядка называется выражение
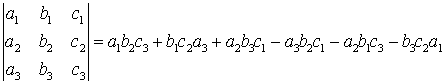
| Правая часть последнего равенства составляется следующим образом. Три слагаемых с плюсом являются произведениями элементов главной диагонали и произведениями элементов, стоящих на параллели к главной диагонали, на элемент из противоположного угла. Три слагаемых с минусом образуются таким же образом относительно второй диагонали. |
Определитель третьего порядка не изменится, если сделать его строки столбцами, записав их в том же порядке:
.
Действительно, при такой замене матрица определителя подвергается преобразованию симметрии относительно главной диагонали. При этом тройки элементов, изображенные закрашенными кружками, не изменяются, а тройки элементов, изображенные кружками со штриховкой, поменяются местами с тройками, изображенными кружками с двойной штриховкой. Поэтому определитель не изменится.
Разложение определителя по элементам строки (столбца).
Вычисление определителя третьего порядка можно свести к вычислению определителей второго порядка.
Вынесем в выражении для определителя третьего порядка за скобки элементы первой строки и запишем выражения в скобках в виде определителей второго порядка:
.
Поменяем порядок столбцов в определителе:
.
Следовательно,
– разложение определителя третьего порядка по элементам первой строки.
Выражение, записанное в правой части, называется разложением определителя третьего порядка по элементам первой строки.
Определитель можно разложить по элементам любой строки или столбца. Для того, чтобы можно было легко составлять такие разложения, вводится понятие алгебраического дополнения.
Дополнительным минором элемента в определителе третьего порядка называется определитель второго порядка, полученный вычеркиванием из данного определителя строки и столбца, содержащих данный элемент. Алгебраическим дополнением элемента называется его дополнительный минор, умноженный на 
, где 
– номер строки, 
– номер столбца, в которых строит данный элемент. Обозначим алгебраическое дополнение элемента 
через 
, алгебраическое дополнение элемента 
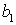через 
и т.д.
Тогда
|
, 
,
.
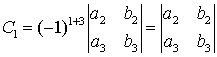Следовательно,
.
Аналогичным образом можно доказать, что
,
,
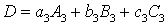и
.
| Знаки перед минорами | 
|
Свойства определителей.
1.3. Свойства определителей 2-го порядка.
1. При перестановке двух строк (столбцов) определитель умножается на 
:
.
2. Определитель с двумя одинаковыми строками (столбцами) равен нулю:
.
3. Общий множитель элементов строки (столбца) можно вынести за знак определителя:
.
4. Если каждый элемент строки (столбца) является суммой двух чисел, то определитель равен сумме двух определителей, в первой из которых на месте сумм стоят первые слагаемые, а во втором – вторые слагаемые:
.
5. Определитель не изменится, если к элементам строки (столбца) прибавить элементы другой строки (столбца), умноженные на любое число:
.
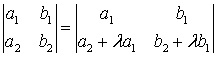Свойства 1-4 доказываются непосредственным подсчетом определителей. При этом достаточно проверять свойства только для строк, так как, по доказанному выше, определитель не изменится, если сделать его строки столбцами.
Докажем свойство 5. Используя последовательно свойства 4, 3, 2, получим:
.
1.4. Свойства определителей 3-го порядка.
1. При перестановке двух строк (столбцов) определитель множится на :
.
Доказательство.
Пусть
, 
.
Разложим каждый из определителей по элементам первой строки.
Получим
, 
.
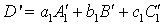Но 
. Аналогично,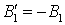 
, 
.
Следовательно,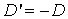 
.
2. Определитель с двумя одинаковыми строками (столбцами) равен нулю:
.
3. Общий множитель элементов строки (столбца) можно выносить за знак определителя:
.
4. Если каждый элемент строки (столбца) является суммой двух чисел, то определитель равен сумме двух определителей, в первом из которых на месте сумм стоят первые слагаемые, а во втором – вторые слагаемые:
.
5. Определитель не изменится, если к элементам строки (столбца) прибавить элементы другой строки (столбца), умноженные на любое число:
.
Свойства 2, 3, 4 доказываются, как и свойство 1, разложением определителя по элементам строки. Свойство 5 доказывается так же, как для определителей второго порядка.
Пример.
6. Сумма произведений элементов строки (столбца) на соответствующие элементы другой строки (столбца) равна нулю.
Докажем, например, что
,
где 
– алгебраические дополнения соответствующих элементов 
в определителе 
.