КИНЕМАТИЧЕСКИЙ АНАЛИЗ ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
Основные понятия
Расчету любой стержневой системы должен предшествовать её кинематический анализ. Стержневая система может иметь практическое применение и рассчитана методами строительной механики только в том случае, если она геометрически неизменяема (ГН).
Геометрически неизменяемые системы в результате внешних воздействий имеют малые деформации. Расчет таких систем ведется по недеформированной схеме (рис. 1.1, 1.2).
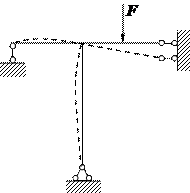
Геометрически изменяемые системы (ГИ) (или механизмы) под силовой нагрузкой имеют конечные перемещения без деформаций (рис. 1.3), следовательно, не могут быть использованы в строительной практике.
Все ГН системы в свою очередь делятся на статически определимые (СО) и статически неопределимые (СН).
Статически определимые системы содержат минимум связей для того, чтобы быть ГН.
Статически неопределимые системы имеют «запас» связей (такие связи еще называют лишними). Эти связи повышают прочность и жесткость конструкции при силовых воздействиях. Разделение стержневых систем на СО и СН играет важную роль для их дальнейшего расчета.
 | |||
|
СО системы могут быть рассчитаны аналитически при помощи уравнений статики. Всегда можно подобрать то или иное уравнение статики для определения опорных реакций в таких системах. Внутренние усилия в них могут быть определены методом сечений с последующим использованием уравнений статики.
Для расчета СН систем недостаточно одних только уравнений статики. Существуют различные методы расчета таких систем (метод сил, метод перемещений и другие). Кроме того, есть различия в поведении СО и СН систем.
Кинематический анализ стержневых систем ставит своей целью выяснить - является ли система ГН либо она ГИ. А если она ГН, то будет ли она СО или СН. Для решения этой задачи необходимо рассмотреть, как образованы плоские стержневые системы, какие внутренние и внешние соединения они содержит. Особую сложность представляют системы, имеющие шарнирные соединения.
Внутренние соединения





|
 Плоские стержневые системы можно представить в виде прямолинейных либо криволинейных стержней, соединённых между собой в узлах. Различают следующие внутренние соединения (внутренние связи):
Плоские стержневые системы можно представить в виде прямолинейных либо криволинейных стержней, соединённых между собой в узлах. Различают следующие внутренние соединения (внутренние связи):
|
ды, следовательно, содержит 1 кинематическую связь.
| |||||
 | |||||
| |||||
| |||||||||
 | |||||||||
 | |||||||||
| |||||||||
|
Опорные соединения.
Неподвижность систем относительно земли обеспечивается опорными связями (опорами). В опорных связях возникают опорные реакции. Совместно с действующими нагрузками, реакции образуют уравновешенную систему сил. При выборе расчетной схемы опоры чаще всего приводят к нескольким типам.

| |||||||
 | |||||||
 | |||||||
 | |||||||

| |||
 |

| |||
 |

 | |||
| |||

 | |||||||||
 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||
 |
Самостоятельн о: Показать деформированные схемы рам. Учитывать при этом только деформации изгиба.
Число степеней свободы системы
Число степеней свободы (W) плоской системы - это количество независимых геометрических параметров, определяющих положение точек системы на плоскости. Под степенью свободы в данном случае понимают подвижность системы под нагрузкой, если эта система имеет бесконечно большую жесткость, то есть перемещается как абсолютно жесткое тело. Тогда, система с одной степенью свободы это механизм, имеющий подвижность в одном направлении и т.д. Исходя из этого, ГН системы должны иметь нулевую либо отрицательную степень свободы. Для определения числа степеней свободы необходимо ввести понятие диска. Диск – плоская ГН система. Это может быть часть стержневой системы, если геометрическая неизменяемость её доказана, либо система в целом. Изначально считается, что на простые диски система делится шарнирами. Конечная цель анализа – доказать, что вся система в целом является диском, неподвижным относительно земли (в случае, если она ГН).
| |||
 | |||



· Д – число дисков;
· Ш – число шарниров, соединяющих диски (удваивается, так как шарнир содержит 2 связи). Если шарнир соединяет несколько дисков, он называется кратным. Количество шарниров в таком узле определяется по формуле Ш=Д-1, где Д – число соединяемых дисков. Например, если в узле k шарниром соединяется 3 диска, а количеств шарниров этом узле – 2.
· С0 – число опорных связей.
1.5
В этом случае использование формулы (1.1) трудоёмко, так как в шарниры в узлах фермы являются кратными (каждый стержень считается диском).
Введём обозначения: У – число узлов фермы, С – число стержней, С0 - число опорных связей.
 Подсчет числа степеней свободы шарнирно-стержневой системы (фермы).
Подсчет числа степеней свободы шарнирно-стержневой системы (фермы).


|
 Число возможных уравнений статики для расчета фермы - 2У (два уравнения статики для каждого узла). Количество неизвестных - С+С0. Условие статической определимости такой системы: 2У=С+С0 . Тогда выражение для подсчета числа степеней свободы фермы будет следующим
Число возможных уравнений статики для расчета фермы - 2У (два уравнения статики для каждого узла). Количество неизвестных - С+С0. Условие статической определимости такой системы: 2У=С+С0 . Тогда выражение для подсчета числа степеней свободы фермы будет следующим

1.6  Условия геометрической неизменяемости системы
Условия геометрической неизменяемости системы
 Определив число степеней свободы системы по выражениям (1.1), (1.2), можно делать следующие выводы. Если W>0 – система геометрически изменяема. Однако, если W£0, окончательный вывод о геометрической неизменяемости системы сделать нельзя (это обязательное, но недостаточное условие). Система может содержать достаточное количество связей для того, чтобы являться ГН, но расположение этих связей может не обеспечивать условие геометрической неизменяемости. Например, балка, показанная на рис. 1.3, б. Она имеет 1 диск, шарниров – 0 и 3 опорные связи. Число степеней свободы посчитанное по выражению (1.1), равное нулю. Однако, балка имеет 1 степень свободы и является геометрически изменяемой. Все её опорные связи параллельны. Здесь нет необходимой связи, препятствующей горизонтальному перемещению этой системы.
Определив число степеней свободы системы по выражениям (1.1), (1.2), можно делать следующие выводы. Если W>0 – система геометрически изменяема. Однако, если W£0, окончательный вывод о геометрической неизменяемости системы сделать нельзя (это обязательное, но недостаточное условие). Система может содержать достаточное количество связей для того, чтобы являться ГН, но расположение этих связей может не обеспечивать условие геометрической неизменяемости. Например, балка, показанная на рис. 1.3, б. Она имеет 1 диск, шарниров – 0 и 3 опорные связи. Число степеней свободы посчитанное по выражению (1.1), равное нулю. Однако, балка имеет 1 степень свободы и является геометрически изменяемой. Все её опорные связи параллельны. Здесь нет необходимой связи, препятствующей горизонтальному перемещению этой системы.
Приведём возможные выводы, которые можно сделать после определения W:
1. W>0 – система геометрически изменяема. Кинематический анализ системы закончен.
2. W=0 – возможно, что система ГН и СО
3. W<0 – возможно, что система ГН и СН.
В последних двух случаях необходимо продолжить анализ системы, рассмотрев её образование.