Матрицы и операции над ними.
Определение. Матрицей размерности m на n называется прямоугольная таблица, составленная из чисел и имеющая m строк и n столбцов.
Обозначения: 
или 
.
Определение. Матрицы называются равными, если они одинаковой размерности и их элементы равны соответственно.
Каждая строка матрицы A размерности m на n представляет собой упорядоченный набор n действительных чисел, а поэтому является вектором арифметического векторного пространства 
. Каждый столбец матрицы A размерности m на n представляет собой упорядоченный набор m действительных чисел, а поэтому является вектором арифметического векторного пространства 
. Таким образом, матрицу размерности m на n можно рассматривать как систему из m векторов пространства , или же – как систему из n векторов пространства . Далее i -ую строку матрицы A обозначим 
, j -ый столбец матрицы A – 
,элемент, расположенный в i- ой строке и j- ом столбце – 
.
Определение. Строчечным пространством матрицы A называется линейная оболочка ее строк. Столбцовым пространством матрицы A называется линейная оболочка ее столбцов:
и 
.
Операции над матрицами и их свойства
Определение. Суммой матриц A и B размерности m на n называется матрица A+B той же размерности, элементы которой определяются правилом:
.
Пример. 
.
Определение. Произведением матрицы A размерности m на n на число 
называется матрица A той же размерности, элементы которой определяются правилом 
.
Пример. 
.
Определение. Произведением матрицы A размерности m на n и матрицы B размерности n на k называется матрица AB размерности m на k, элементы которой определяются правилом 
, т.е.
.
Замечание. При умножении матриц важно, чтобы число элементов в строке (число столбцов) первого множителя совпадало с числом элементов в столбце (число строк) второго множителя, иначе векторы и 
нельзя умножить скалярно.
Пример. Произведение матриц 
и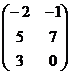 
не существует.
, но произведение матриц 
и не существует.
Определение. Матрицей, транспонированной к матрице A размерности m на n, называется матрица 
размерности n на m, элементы которой определяются правилом 
.
Пример. 
.
Таким образом, чтобы протранспонировать матрицу, нужно ее строки записать как столбцы новой матрицы или столбцы записать как строки.
Прежде, чем перейти к рассмотрению и доказательству свойств операций над матрицами, докажем вспомогательное утверждение.
Лемма (о строчечном и столбцовом пространстве произведения матриц). Строчечное пространство произведения двух матриц является подпространством строчечного пространства второго множителя. Столбцовое пространство произведения двух матриц является подпространством столбцового пространства первого множителя.
Доказательство. Пусть A – матрица размерности m на n, B – матрица размерности n на k. Тогда AB – матрица размерности m на k, а поэтому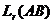 
, 
– подпространства 
. Таким образом чтобы доказать первую часть леммы нужно показать, что имеет место включение 
. Строчечное пространство матрицы AB есть линейная оболочка ее строк, а значит, достаточно показать, что всякая строка матрицы AB принадлежит строчечному пространству матрицы B, т.е. является линейной комбинацией строк матрицы B.
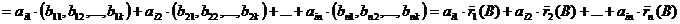– линейная комбинация строк матрицы B.
Чтобы доказать вторую часть леммы нужно показать, что имеет место включение 
. Проведите рассуждения самостоятельно ■
Следствие 1. Если строки матрицы C линейно выражаются через строки матрицы B, то существует матрица A, такая что С=AB.
Следствие 2. Если столбцы матрицы C линейно выражаются через столбцы матрицы A, то существует матрица B, такая что С=AB.
Доказательство этих утверждений проведите самостоятельно.
Теорема (свойства операций над матрицами).
1. Сложение матриц коммутативно и ассоциативно: 
и 
.
2. Умножение матрицы на число дистрибутивно относительно сложения матриц и перестановочно с умножением матриц 
и 
.
3. Умножение матриц дистрибутивно относительно сложения матриц и ассоциативно: 
и 
.
4. 
. 5. 
. 6. 
7. 
Доказательство. Для доказательства равенств воспользуемся определением равенств матриц и покажем, что матрицы левой и правой части каждого равенства имеют одинаковые размерности и элементы их равны соответственно.
1. Пусть A и B – матрицы размерности m на n. По определению суммы матриц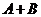 
и 
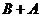– это матрицы той же размерности m на n. Снова применяя определение суммы, получим 
.
Пусть A, B и C – матрицы размерности m на n. По определению суммы двух матриц 
и 
– это матрицы той же размерности m на n. Применяя опять определение суммы, получим
.
2. Докажите самостоятельно.
3. Тождество докажите самостоятельно. Покажем, что . Пусть A – матрица размерности m на n, B – матрица размерности n на k, C – матрица размерности k на s. Тогда по определению произведения матриц AB – матрица размерности m на k, 
– матрица размерности m на s; BC – матрица размерности n на s, 
– матрица размерности m на s. Итак, матрицы и имеют одинаковые размерности.
Рассмотрим произвольный элемент матрицы левой части равенства:
.
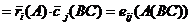4. Пусть A – матрица размерности m на n. Тогда по определению транспонированной матрицы – матрица размерности n на m., а 
– матрица размерности m на n. Рассмотрим произвольный элемент матрицы левой части равенства:
.
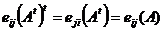5. – 7. Докажите самостоятельно.