Серия 20. Десятичная запись числа.

Серия 17. Геометрическая.

1. Проверяя, что кусок материи имеет форму квадрата, швея перегибает его по каждой диагонали и убеждается, что края каждый раз совпадают. Достаточна ли такая проверка?
2. Даны 100 отрезков. Известно, что из любых трех можно составить треугольник. Все длины – натуральные. Длины двух первых отрезков равны 7 и 4. Какие длины могут иметь остальные отрезки?
3. Разрежьте квадрат на 3 части, из которых можно сложить треугольник с 3 острыми углами и тремя различными сторонами.
4. Могут ли расстояния от некоторой точки на плоскости до вершин некоторого квадрата быть равными 1, 4, 7 и 8?
5. Прямоугольный лист бумаги согнули, совместив вершину с серединой противоположной короткой стороны. Оказалось, что треугольники I и II равны. Найдите длинную сторону прямоугольника, если короткая равна 8.

 

6. Квадрат разбит на пять прямоугольников так, как показано на рисунке. Площади угловых прямоугольников равны. Докажите, что центральный прямоугольник – квадрат.

1. Фигура на рисунке составлена из квадратов. Найдите сторону левого нижнего, если сторона самого маленького равна 1.

 

 

1. Можно ли накрыть равносторонний треугольник двумя меньшими равносторонними треугольниками?

Серия 18. Письменная.

1. Не находя суммы 52715223 + 71337651 + 53258554 + 633164334 + 71574116 + 4325988, выберите верный ответ: а) 886375457; б) 886375478; в) 886375866; г) 86375942. Поясните, как вы его выбрали.

2. Некоторые семиклассники взяли из 313 фломастеры для стенгазеты. Из них несколько мальчиков взяли по целой пачке из 6 фломастеров, несколько девочек забрали по 8 фломастеров разных цветов, а восьми опоздавшим досталось по фломастеру синего цвета. В конце недели Михаил Александрович хочет собрать с семиклассников 155 фломастеров. Сочтут ли школьники это требование выполнимым?

3. Каждый следующий день смены семиклассник получает в два раза меньше комариных укусов, чем в предыдущий. Может ли он за два дня подряд получить 2000 укусов?

4. ЮМШастик Саша охотился на комаров. В первый день ему удалось убить только двоих, но с каждым днем его квалификация повышалась и ему удавалось убивать вдвое больше комаров, чем в предыдущий. Мог ли он в двадцать пятый день убить 33554434 комара?

5. Какие из утверждений верны:
а) если число при делении на 8 дает остаток 3, то при делении на 4 оно также дает остаток 3;
б) если число при делении на 4 дает остаток 3, то при делении на 8 остаток сохраняется;
в) если число при делении на 15 дает остаток 7, то при делении на 5 остаток не равен 3;
г) если число при делении на 15 дает остаток 3, то при делении на 9 остаток не равен 6?

6. Генерал построил солдат в колонну по 4, но при этом солдат Иванов остался лишним. Тогда генерал построил солдат в колонну по 5. И снова Иванов остался лишним. Когда же и в колонне по 6 Иванов остался лишним, генерал посулил ему наряд вне очереди, после чего в колонне по 7 Иванов нашел себе место и никого лишнего не осталось. Какое наименьшее количество солдат могло быть у генерала?

7. Дождь начался в полночь и лил ровно 10000 минут. Могло ли случиться, что сразу после этого выглянуло солнце?

8. На сколько нулей заканчивается число 2000!?

Серия 18. Набиваем руку.

1. Лиза нарисовала на доске семь котиков. Потом в аудиторию пришли 33 ЮМШовца. Каждый из них или стёр одного котика, или дорисовал нового. Могло ли в конце остаться три котика?
2. Не вычисляя произведения 2013 · 15 · 77, определите, делится ли оно на 2, 3, 9, 35, 55, 80, 6039.
3. Мария Михайловна написала на доске 50 чисел. Игорь заметил, что сумма любых 49 чисел нечётна. Чётна или нечётна сумма всех чисел?

3. Найдите последнюю цифру числа
а) 2001²ºº¹; б) 549⁴⁹; в) 345673³⁷⁶⁵⁴³; г) .

1. В последовательности цифр каждая цифра, начиная с пятой, равна последней цифре суммы четырех предыдущих. Последовательность начинается с цифр 1234096. Может ли в ней встретиться комбинация цифр 1999?
2. Найдите две последние цифры числа а) 1999²⁰⁰⁰; б) 16²⁰⁰⁰.
3. а) Докажите, что найдется число вида 111…11000..00, делящееся на 2013.
   б) Докажите, что найдется число, состоящее из одних единиц, делящееся на 2013.
4. На сколько нулей заканчивается число 1000!?
5. Найдите последнюю ненулевую цифру числа 1000!.
6. натуральное число делится на 42. Сумма цифр не вошедших в него равна 25. Докажите, что в этом числе есть повторяющиеся цифры.
7. Будем говорить, что натуральное число а загадочнее числа b, если при делении 839 на а получается остаток b. Докажите, что не существует 10 пордяд идущих натуральных чисел, каждое из которых загадочнее предыдущего

Серия 19. Формула Пика.

Вершины многоугольника расположены в узлах клетчатой бумаги. Внутри него лежит n узлов, а на границе m узлов. Тогда площадь этого многоугольника равна n + m/2 – 1.

 

1. Проверьте формулу Пика для прямоугольника со сторонами, идущими по линиям сетки.
2. Докажите формулу Пика для многоугольника со сторонами, идущими по линиям сетки.
3. Докажите формулу Пика для прямоугольного треугольника с катетами, на линиям сетки.
4. Докажите формулу Пика для многоугольника, составленного из двух многоугольников, для которых формула Пика уже доказана.
5. Пусть многоугольник, для которого формула Пика уже проверена, составлен из двух многоугольников. Докажите, что если формула Пика выполняется для одного из них, то она выполняется и для другого.
6. Использовав пункты 3 и 5, докажите формулу Пика для произвольного треугольника с вершинами в узлах клетчатой бумаги.
7. Докажите, что любой выпуклый многоугольник можно разбить диагоналями на треугольники.
8. Докажите, что любой (не обязательно выпуклый) многоугольник можно разбить диагоналями на треугольники.
9. Докажите формулу Пика для произвольного многоугольника.

Серия 20. Десятичная запись числа.

1. В числе 513879406 вычеркните 4 цифры так, чтобы оставшиеся цифры в том же порядке составили наибольшее число; наименьшее число.

2. Может ли двузначное число равняться сумме своих цифр?

3. Найдите все четырехзначные числа, две средние цифры которых образуют число, в 5 раз большее числа тысяч и в 3 раза большее числа единиц.

4. Шифр замка – автомата ­– семизначное число, три первые цифры которого одинаковые, остальные четыре цифры так же одинаковые. Сумма все цифр этого числа – число двузначное, первая цифра которого совпадает с первой цифрой шифра, а последняя - с последней. Найдите этот шифр.

5. Андрея попросили назвать номер квартиры, которую получила его семья в новом доме. Он ответил, что этот номер выражается числом, которое в семнадцать раз больше числа, стоящего в разряде единиц номера. Каков же номер этой квартиры?

6. Из пятизначного числа вычли такое же, но записанное в обратном порядке. Докажите, что получившееся число делится на 11.

7. Найдите число, сумма цифр которого равна разности между 328 и искомым числом.

8. Используя каждую из девяти цифр 1,2,…,9 по одному разу, запишите три такие числа, чтобы сумма их была наибольшей из всех возможных, а разность при этом между большим и меньшим числами была как можно меньше. Найдите эту сумму и разность.

9. Известно, что число, выражающее количество учащихся, является наибольшим из всех таких чисел, у которых любые две соседние цифры образуют каждый раз число, делящееся без остатка на 23. Найдите его.

Серия 21. С праздником Весны! Или просто «Сколько?» 1. В классе мальчики дарили девочкам цветы. Известно, что каждый из 18 мальчиков принес 6 цветков. Сколько девочек в классе, если каждая в результате стала обладательницей букета из 9 цветов?2. Сколько способов добраться из города A в город C, если нельзя дважды посещать один город? а) б) в) 3. У людоеда в подвале томятся 25 пленников.а. Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин?б. А сколько есть способов выбрать троих, чтобы отпустить на свободу?4. Сколькими способами можно прочитать в таблице слово а) КРОНА; б) КОРЕНЬ, начиная с буквы «K» и двигаясь вправо или вниз? 5. Сколькими способами можно расселить 9 человек в три комнаты: трехместную, двухместную и четырехместную?6. Есть 6 мальчиков и 6 девочек, детей расставляют по кругу так, чтобы мальчики и девочки чередовались. Сколько способов их расставить, если а. надо расставить всех 12 детей;б. надо расставить каких-то 8 детей.

7. Сколькими способами можно переставить буквы слова «ПЕЛИКАН», чтобы гласные буквы стояли в алфавитном порядке?

8. На прямой отмечено 10 точек, а на параллельной ей прямой – 11 точек. Сколько существует

а. треугольников с вершинами в этих точках;

б. четырехугольников с вершинами в этих точках?

9. Можно ли шесть разновесных одинаковых по виду гирек гарантировано расположить в порядке возрастания за пять взвешиваний?

Серия 22. Да здравствует индукция! И никак иначе! 10. Неравенство треугольника гласит, что для любых трёх точек A₁, A₂, A₃ выполнено: A₁A₂ + A₂A₃ ≥ A₁A₃. Докажите, что для любого n длина n-звенной ломаной не меньше длины отрезка между её концами. 11. Докажите, что любую сумму, начиная с 8 тугриков, можно выплатить купюрами по 3 тугрика и 5 тугриков.12. Докажите, что для любого n верна формула: 1²+2²+…+n²=n(n+1)(2n+1)/6.13. У бородатого многоугольника во внешнюю сторону растет щетина. Его пересекает n прямых, на каждой из которых с одной из сторон тоже растет щетина. В результате многоугольник оказался разбитым на некоторое число частей. Докажите, что хотя бы одна из частей окажется бородатой снаружи. 14. Плоскость поделена на области несколькими прямыми. Докажите, что эти области можно раскрасить в два цвета так, чтобы любые две соседние области были раскрашены в различные цвета. (Соседними считаются области, имеющие общий участок границы.)15. На доске написаны сто цифр: нули и единицы (в произвольной комбинации). Разрешается выполнять две операции: (1) заменять первую цифру (нуль на единицу и наоборот); (2) заменять цифру, стоящую после первой единицы. Например, в последовательности 0011001... можно заменить первую цифру или четвёртую. Докажите, что с помощью нескольких таких замен можно получить любую комбинацию из ста нулей и единиц.16. Незнайке сообщили некоторое число a. Он вычислил n чисел: a+a^-1, a²+a^-2, a³+a^-3, …, aⁿ+a^-n и все они оказались целыми. Незнайка очень устал. Помогите ему доказать, что aⁿ⁺¹+a^-n-1тоже целое.

Серия 23. Прочная?

1. Камиль задумал пятизначное число, кратное 9, и посчитал сумму его цифр. Потом он проделал эту же операцию с полученным числом. Какое число получил в результате Камиль?
2. Существует ли прочное разбиение полоски 3´100 на доминошки?
3. Есть 10 монет, одна из которых – фальшивая. Имеется также детектор, который за одну операцию исследует 4 монеты и указывает на одну из них. Известно, что если среди исследуемых монет есть фальшивая, то детектор указывает на неё. Однако если фальшивой монеты среди исследуемых нет, то детектор может указать на любую монету. За какое наименьшее число операций удастся заведомо определить фальшивую монету?
4. Существует ли прочное разбиение прямоуольника 6´8 на доминошки?
5. На дистанции в 2 мили жираф обгоняет носорога на 1/4 мили, а носорог гиппопотама — на 1/8 мили. На сколько жираф обгонит гиппопотама на дистанции 2 мили?

6. Существует ли прочное разбиение квадрата 6´6 на доминошки?

1. Назовем трехзначное число “горкой”, если в нем цифра в разряде десятков больше любой из двух оставшихся, и “ямкой”, если в нем цифра в разряде десятков меньше любой из двух оставшихся. Каких чисел больше – “горок” или “ямок”, и на сколько?
2. Существует ли прочное разбиение полоски 4´100 на доминошки?
3. Может ли число, записываемое при помощи 100 нулей, 100 единиц и 100 двоек, быть точным квадратом?
4. Есть 100 монет, одна из которых – фальшивая. За какое наименьшее число операций удастся с помощью детектора из задачи 3 заведомо определить фальшивую монету?

Серия 24. Инвариантная.

1. На сосне растут 8 бананов и 7 апельсинов. Если сорвать два 23одинаковых фрукта, то на сосне тут же вырастет один банан, а если сорвать два разных – вырастет один апельсин. Срывать фрукты по одному нельзя. Можно ли сорвать фрукты с сосны так, чтобы последним был банан?
2. Черный ящик работает так: любые три числа a, b и c, попадающие в него, он перерабатывает в числа a + b – c, b + c – a, c + a – b. Можно ли с помощью этого ящика из чисел 1, 3, 9 получить числа –11111111113, 3, 11111111111?
3. На доске написаны числа от 1 до 100. Разрешается стереть любые два числа и написать вместо них их разность. Может ли после 99 таких операций остаться число 1?
4. На нижней половине доски 10x10 стоят шашки (50 шт.) Разрешается перепрыгнуть шашкой через соседнюю с ней, если следующая клетка свободна. Можно ли собрать все шашки на верхней половине доски?
5. В одной вершине куба написано число 1, в остальных — нули. Можно прибавлять по единице к числам в концах любого ребра. Можно ли добиться, чтобы все числа делились на 3?
6. Можно ли операциями «умножить на 7» и «прибавить 6» получить из единицы число 2006?
7. Есть куча из 1001 камня. Ход состоит в том, что из какой-нибудь кучи, где лежит более одного камня, выкидывают один камень на помойку, а затем любую кучу делят на две произвольные части. Можно ли через неско.лько ходов получить лишь кучи, состоящие из трех камней?

8. На доске написано целое число, большее 1. Разрешённые операции: если на доске уже есть число A, можно дописать ещё числа 2A и 3A.

a. Докажите, что сумма чисел на доске всегда будет составной.

b. Можно ли получить несколько чисел с общей суммой 2007?

Серия 25. Числа-числа! И все такие разные… 1. Что больше: а. 50⁵⁰ или 216³³?б. 2⁶⁵ или 3⁵⁶? в. 6⁶⁵ или 9⁵⁶?2. Известно, что a ³ делится на 1620. Укажите максимальное натуральное число, на которое наверняка делится a 3. Найдите все натуральные числа, в 12 раз большие своей суммы цифр.4. Докажите, что число делится на 7 для любого натурального n 5. Решите в натуральных числах уравнение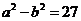

6. Все простые числа, не превосходящие простого числа р, разбили на две группы и нашли произведение всех чисел в каждой из групп, после чего из большего произведения вычли меньшее. Эта разность оказалась меньше р. Докажите, что она равна 1.

7. Найдите сумму: .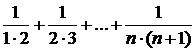

8. а, b и c ‑ натуральные числа такие, что а ³ делится на b, b ³ делится на c, а c ³ делится на a. Докажите, что (a+b+c)¹³ делится на abc.

Серия 26. С Днем рождения Макар!

Ура! Игротека!!!

1. Шоколадка представляет собой прямоугольник 5 × 8, разделённый бороздками на 40 квадратиков. Макар и Саша по очереди разламывают её на части по бороздкам: за один ход можно разломить любой из кусков на два. Макар ходит первым, кто не может сделать хода – проигрывает. Кто выигрывает при правильной игре?

2. Двое играют, поочередно выставляя крестики и нолики на квадратном поле 9 9. В конце каждый получает очко за каждую строку и столбец, в которых его знаков больше. Кто выигрывает при правильной игре?

3. Игра начинается с числа 30. За ход можно уменьшить число на любой из его делителей. Проигрывает тот, кто получит 0. Кто выигрывает при правильной игре?

4. Двое играют в следующую игру: первый выбирает любое поле на доске 8×8 и ставит туда коня. Дальше они по очереди, начиная со второго делают ход при условии, что на эту клетку раньше никто не вставал. Проигрывает тот, кто не может сделать ход. Кто выигрывает при правильной игре?

5. Соня и Полина играют в такую игру: имеется доска 100´100. Соня каждым ходом закрашивает одну клетку, а Полина – уголок из трёх клеток. Соня ходит первой. Кто выиграет при правильной игре?

6. На столе лежит куча из 2011 монет. Сеня и Макар по очереди берут монеты из кучи. Начинает Сеня. За один ход можно брать одну или две монеты. Игра заканчивается, когда все монеты из кучи взяты. Выигрывает тот, у кого на руках по окончании игры окажется нечетное число монет. Кто выиграет при правильной игре?

7. У прямоугольной доски 10×11 выпилили все внутренние клетки так, что получилась рамка шириной в одну клетку. Разрешается вырезать любой прямоугольник 1× п так, чтобы оставшаяся фигура не развалилась на 2 части. Тот, кто не может сделать ход, – проигрывает. Макар выбирает, первым или вторым он будет ходить. Помогите ему.

8. В музее 100 картин. Двое смотрителей дежурят по очереди. В свое дежурство смотритель переворачивает ровно 5 картин (у каждой картины есть ровно 2 положения). Проигрывает тот, после чьего хода ситуация повторится. Кто выигрывает при правильной игре и как ему для этого играть?