5) МЕТОД КОРРЕЛЯЦИОННЫХ ПЛЕЯД
Терентьевым был изобретен метод корреляционных плеяд. Суть метода такова. Визуально результаты классификации можно представить в виде цилиндра, рассеченного плоскостями, перпендикулярными его оси. Плоскости соответствуют его уровням (от 0 до 1 с шагом 0,1), на которых объединяются параметры или объекты, подлежащие классификации, поэтому метод напоминает метод ближней связи, но с фиксированными уровнями объединения. Графически результаты классификации изображают в виде окружностей – срезов (плеяд) упомянутого выше корреляционного цилиндра. На окружностях отмечают классифицируемые объекты. Связи между классифицированными объектами указывают путем соединения хордами точек окружности, соответствующих объектам.
6) ВРОЦЛАВСКАЯ ТАКСОНОМИЯ
Результатом работы программы, использующей метод максимального корреляционного пути, являются пары чисел, указывающие порядок «соединения» подлежащих классификации параметров или объектов, наиболее близких попарно. Получающийся кратчайший замкнутый путь можно отобразить графически в виде оптимального дерева (дендрита), как это описано в следующем разделе.
Классифицируемы могут быть параметры либо объекты. Метод похож на метод ближайшей связи, однако относится к алгоритмам типа разрезания графа и напоминает методы вроцлавской таксономии. Если в качестве меры сходства применяется коэффициент корреляции, получается метод максимального корреляционного пути.
Методы иерархической группировки (численной таксономии) исходных множеств получили название кластер-анализа, то есть анализа групп. Первоначально они применялись в биологии и палеонтологии, а в настоящее время широко используются в различных отраслях геолого-минералогических наук, в частности, при классификации парагенетических ассоциаций элементов земной коры.
Термин кластерный анализ (впервые ввел Tryon, 1939) в действительности включает в себя набор различных алгоритмов классификации. Общий вопрос, задаваемый исследователями во многих областях, состоит в том, как организовать наблюдаемые данные в наглядные структуры, то есть развернуть таксономии. Например, биологи ставят цель разбить животных на различные виды, чтобы содержательно описать различия между ними. В соответствии с современной системой, принятой в биологии, человек принадлежит к приматам, млекопитающим, амниотам, позвоночным и животным. Заметьте, что в этой классификации, чем выше уровень агрегации, тем меньше сходства между членами в соответствующем классе. Человек имеет больше сходства с другими приматами (то есть с обезьянами), чем с «отдаленными» членами семейства млекопитающих (например, собаками) и т.д. Фактически, кластерный анализ является не столько обычным статистическим методом, сколько «набором» различных алгоритмов «распределения объектов по кластерам». Существует точка зрения, что в отличие от многих других статистических процедур, методы кластерного анализа используются в большинстве случаев тогда, когда вы не имеете каких-либо априорных гипотез относительно классов, но все еще находитесь в описательной стадии исследования. Следует понимать, что кластерный анализ определяет «наиболее возможно значимое решение». Поэтому проверка статистической значимости в действительности здесь неприменима, даже в случаях, когда известны p-уровни (как, например, в методе K-средних).
Задача кластер-анализа сводится к разбиению множества элементов корреляционной матрицы признаков [ R ] на группы таким образом, чтобы в них объединялись объекты с наивысшими значениями характеристик сходства, а разобщенные группы оставались бы при этом максимально изолированными по данному признаку. В качестве меры сходства могут использоваться непосредственно парные коэффициенты корреляции, m -мерное эвклидово расстояние или другие дистанционные коэффициенты.
МЕТРИКИ
Мера сходства между элементами множеств (типа расстояния) называется метрикой, если она удовлетворяет определенным условиям: симметрии, неравенству треугольника, различимости нетождественных объектов и неразличимости тождественных объектов.
Метрика Минковского
Наиболее общей метрикой является метрика Минковского. Степень разности значений можно выбрать в пределах от 1 до 4. Если эту степень взять равной 2, то получим евклидово расстояние. Расстояние Минковского равно корню r-ой степени из суммы абсолютных разностей пар значений взятых в r-ой степени:
distance(x,y) = {Si (xi - yi) r }1/ r
Евклидова метрика
Это наиболее часто выбираемый тип расстояния. Это просто геометрическое расстояние в многомерном пространстве. Евклидова дистанция между двумя точками х и у – это наименьшее расстояние между ними. В двух- или трёхмерном случае – это прямая, соединяющая данные точки. Если в метрике Минковского положить r =2, мы получим стандартное евклидово расстояние (евклидову метрику)
distance(x,y) = {Si (xi - yi)2 }½
Квадратная евклидова метрика (квадрат евклидова расстояния)
Дает больший по сравнению с евклидовой метрикой вес объектов, которые размещаются более обособленно. Благодаря возведению в квадрат при расчёте лучше учитываются большие разности
distance(x,y) = Si (xi - yi)2
Манхеттенское расстояние
Это расстояние просто среднее различие поперечных измерений. При r =1 метрика Минковского дает манхеттенское расстояние (метрику города, city block, Manhattan distance). Эта дистанционная мера, называемая также дистанцией Манхэттена или в шутку – дистанцией таксиста, определяется суммой абсолютных разностей пар значений. Для двумерного пространства это не прямолинейное евклидова расстояние между двумя точками, а путь, который должен преодолеть Манхэттенский таксист, чтобы проехать от одного дома к другому по улицам, пересекающимся под прямым углом
distance(x,y) = Si |xi - yi|
Чебышевское расстояние
Эта мера расстояния может быть соответствующая в случаях, когда каждый хочет определить два объекта как «различные», если они различны на любом из измерений. Разностью двух наблюдений является абсолютное значение максимальной разности последовательных пар переменных, соответствующих этим наблюдениям.
distance(x,y) = Maximum|xi - yi|
Пользовательская метрика (степенное расстояние)
Это обобщенный вариант расстояния Минковского. Это расстояние, называемое также степенным расстоянием, равно корню r-ой степени из суммы абсолютных разностей пар значений взятой в р-ой степени:
distance(x,y) = (Si |xi - yi|p)1/r,
где r и p - определяемые пользователем параметры. Здесь как для корня, так и для степени суммы можно выбирать значения от 1 до 4. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если r и p равны 2, то это расстояние равно евклидовому расстоянию.
Процент различия (несогласия)
Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется как:
distance(x,y) = (Number of xi ¹ yi)/i
ПРАВИЛА ОБЪЕДИНЕНИЯ ИЛИ СВЯЗИ
На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой. Однако когда связываются вместе несколько объектов, возникает вопрос, как следует определить расстояния между кластерами? Другими словами, необходимо правило объединения или связи для двух кластеров. Здесь имеются различные возможности: например, вы можете связать два кластера вместе, когда любые два объекта в двух кластерах ближе друг к другу, чем соответствующее расстояние связи. Другими словами, вы используете «правило ближайшего соседа» для определения расстояния между кластерами; этот метод называется методом одиночной связи. Это правило строит «волокнистые» кластеры, то есть кластеры, «сцепленные вместе» только отдельными элементами, случайно оказавшимися ближе остальных друг к другу. Как альтернативу вы можете использовать соседей в кластерах, которые находятся дальше всех остальных пар объектов друг от друга. Этот метод называется метод полной связи. Существует также множество других методов объединения кластеров, подобных тем, что были рассмотрены.
Одиночная связь (метод ближайшего соседа). Как было описано выше, в этом методе расстояние между двумя кластерами определяется расстоянием между двумя наиболее близкими объектами (ближайшими соседями) в различных кластерах. Это правило должно, в известном смысле, нанизывать объекты вместе для формирования кластеров, и результирующие кластеры имеют тенденцию быть представленными длинными «цепочками».
Полная связь (метод наиболее удаленных соседей). В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (то есть «наиболее удаленными соседями»). Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных «рощ». Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является «цепочечным», то этот метод непригоден.
Невзвешенное попарное среднее. В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные «рощи», однако он работает одинаково хорошо и в случаях протяженных («цепочного» типа) кластеров. Отметим, что в своей книге Снит и Сокэл (Sneath, Sokal, 1973) вводят аббревиатуру UPGMA для ссылки на этот метод, как на метод невзвешенного попарного арифметического среднего - unweighted pair-group method using arithmetic averages.
Взвешенное попарное среднее. Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (то есть число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован (скорее даже, чем предыдущий), когда предполагаются неравные размеры кластеров. В книге Снита и Сокэла (Sneath, Sokal, 1973) вводится аббревиатура WPGMA для ссылки на этот метод, как на метод взвешенного попарного арифметического среднего - weighted pair-group method using arithmetic averages.
Невзвешенный центроидный метод. В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести. Снит и Сокэл (Sneath and Sokal (1973)) используют аббревиатуру UPGMC для ссылки на этот метод, как на метод невзвешенного попарного центроидного усреднения - unweighted pair-group method using the centroid average.
Взвешенный центроидный метод (медиана). Э тот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (то есть числами объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего. Снит и Сокэл (Sneath, Sokal 1973) использовали аббревиатуру WPGMC для ссылок на него, как на метод невзвешенного попарного центроидного усреднения - weighted pair-group method using the centroid average.
Метод Варда. Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. Подробности можно найти в работе Варда (Ward, 1963). В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.
ВИЗУАЛИЗАЦИЯ РЕЗУЛЬТАТОВ КЛАСТЕРНОГО АНАЛИЗА
После проведения классификации рекомендуется визуализировать результаты кластеризации путем построения дендрограммы (дендограммы). Для большого числа объектов такая визуализация является единственным способом получить представление об общей конфигурации объектов.
Хотя от графического представления данных во многих методах можно отказаться, иерархические методы кластерного анализа становятся более наглядными, если результаты расчета представить в виде специального графика, называемого дендрограммой (дендограммой).
Предположим, после применения одного из иерархических методов получены результаты классификации в виде величин связи для пар объектов. Идея построения дендрограммы очевидна – пары объектов соединяются в соответствии с уровнем связи, отложенным по оси ординат (рис. VII.1).
Рис. VII.1. Дендрограмма иерархического метода
Диаграмма начинается с каждого объекта в классе (в нижней части диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы «ослабляете» ваш критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к решению об объединении двух или более объектов в один кластер. В результате, вы связываете вместе всё большее и большее число объектов и агрегируете (объединяете) все больше и больше кластеров, состоящих из все сильнее различающихся элементов. Окончательно, на последнем шаге все объекты объединяются вместе. На этих диаграммах вертикальные оси представляют расстояние объединения (в горизонтальных древовидных диаграммах горизонтальные оси представляют расстояние объединения). Так, для каждого узла в графе (там, где формируется новый кластер) вы можете видеть величину расстояния, для которого соответствующие элементы связываются в новый единственный кластер. Когда данные имеют ясную «структуру» в терминах кластеров объектов, сходных между собой, тогда эта структура, скорее всего, должна быть отражена в иерархическом дереве различными ветвями. В результате успешного анализа методом объединения появляется возможность обнаружить кластеры (ветви) и интерпретировать их.
По оси абсцисс располагаются символические обозначения объектов исследования (векторов матрицы), а по оси ординат – минимальные значения дистанционных коэффициентов, соответствующих каждому шагу классифицирующей процедуры. Таким образом, ось ординат используется для масштабного представления иерархических уровней группирования.
Наглядность и содержательная ценность древовидных графов существенно повышаются, если в них отражена информация не только о тесноте внутригрупповых связей, но и о межгрупповых расстояниях h. Такой дендровидный граф, учитывающий не только внутригрупповые расстояния, но и средние расстояния между группами, называется дендрографом.
Рудные тела редкометалльного месторождения приурочены к зонам натровых метасоматитов (альбититов). В результате детального изучения минерального состава метасоматитов было установлено, что на месторождении развиты альбититы двух типов. Причем редкометалльное оруденение характерно лишь для одного из них. По химическому составу рудные и безрудные альбититы весьма близки, поэтому различить их по содержанию отдельных химических элементов не удается. Однако некоторые различия в минеральном составе проявляются в особенностях корреляционных связей между элементами. Наглядно эти различия отражаются на графах (рис. VII.2, а, б) и дендрограммах (рис. VII.2, в, г). В качестве меры близости элементов при построении дендрограмм в данном случае используются непосредственно парные коэффициенты корреляции, рассчитанные по 50 пробам, отобранным из рудных и безрудных альбититов, тип которых однозначно определен минералогическими исследованиями. Предельное значение коэффициента корреляции для доверительной вероятности 0,95 при объеме выборок в 50 проб равен 0,28. Поэтому для целей классификации целесообразно сравнивать лишь те группы, для которых коэффициенты корреляции, отражающие тесноту внутригрупповой связи, превышают эту величину.
Для обеих дендрограмм характерна группа, объединяющая фосфор и редкоземельные элементы, что, по-видимому, обусловлено присутствием в альбититах обоих типов апатита, в составе которого отмечены повышенные концентрации этих элементов.
Основной отличительной особенностью безрудных альбититов является тесная ассоциация сидерофильных элементов (Ni—Cr—Ti—Со), которая в рудных альбититах распадается.
Для рудных альбититов характерна ассоциация халькофильных элементов (Pb—Zn), в то время как в безрудных альбититах корреляционная связь между этими элементами отрицательная. Таким образом кластер-анализ позволяет оперативно и достаточно надежно определить тип альбититов по результатам спектральных анализов, не прибегая к детальному изучению шлифов.
Рис VII.2. Характеристики корреляционных связей между содержаниями химических элементов в альбититах:
а —граф по безрудным альбититам; б —граф по рудным альбититам; в —дендрограмма по безрудным альбититам; г —дендрограмма по рудным альбититам
МЕТОД K-СРЕДНИХ
Этот метод кластеризации существенно отличается от таких агломеративных методов, как древовидная кластеризация. Предположим, вы уже имеете гипотезы относительно числа кластеров (по наблюдениям или по переменным). Вы можете указать системе образовать ровно три кластера так, чтобы они были настолько различны, насколько это возможно. Это именно тот тип задач, которые решает алгоритм метода K-средних. В общем случае метод K-средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга.
С вычислительной точки зрения вы можете рассматривать этот метод, как дисперсионный анализ «наоборот». Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы: (1) - минимизировать изменчивость внутри кластеров, и (2) - максимизировать изменчивость между кластерами. Данный способ аналогичен методу «дисперсионный анализ наоборот» в том смысле, что критерий значимости в дисперсионном анализе сравнивает межгрупповую изменчивость с внутригрупповой при проверке гипотезы о том, что средние в группах отличаются друг от друга. В кластеризации методом K-средних программа перемещает объекты (то есть наблюдения) из одних групп (кластеров) в другие для того, чтобы получить наиболее значимый результат при проведении дисперсионного анализа
Обычно, когда результаты кластерного анализа методом K-средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга. В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F -статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискриминирует кластеры.
ФАКТОРНЫЙ АНАЛИЗ
Основным объектом исследования методами факторного анализа является корреляционная матрица, построенная с использованием коэффициента корреляционного отношения Пирсона (для количественных признаков). Предлагается также использование других коэффициентов типа корреляции, предназначенных для порядковых, качественных и смешанных признаков, но опыта в этой области пока недостаточно. Основным требованием к построенной матрице является ее положительная полуопределенность. Эрмитова матрица называется положительно полуопределенной, если все ее главные миноры неотрицательны. Из данного свойства как раз и следует неотрицательность всех собственных значений.
Методами факторного анализа решаются три основных вида задач:
· отыскание скрытых, но предполагаемых закономерностей, которые определяются воздействием внутренних или внешних причин на изучаемый процесс;
· выявление и изучение статистической связи признаков с факторами или главными компонентами;
· сжатие информации путем описания процесса при помощи общих факторов или главных компонент, число которых меньше количества первоначально взятых признаков (параметров), однако с той или иной степенью точности обеспечивающих воспроизведение корреляционной матрицы.
Следует пояснить, что в факторном анализе понимается под сжатием информации. Дело в том, что корреляционная матрица получается путем обработки исходного массива данных. Предполагался, что та же самая корреляционная матрица может быть получена с использованием тех же объектов, но описанных меньшим числом параметров. Таким образом, якобы происходит уменьшение размерности задачи, хотя на самом деле это не так. Это не сжатие информации и в общепринятом смысле – восстановить исходные данные по корреляционной матрице нельзя.
Коэффициенты корреляции, составляющие корреляционную матрицу, по умолчанию вычисляются между параметрами (признаками, тестами), а не между объектами (индивидуумами, лицами), поэтому размерность корреляционной матрицы равна числу параметров. Это так называемая техника R. Однако может быть, например, изучена корреляция между объектами (точнее, их состояниями, описываемыми векторами параметров). Эта методика называется техникой Q. Проведение факторного анализа техникой Q обосновано тем, что состояния объектов могут иметь общую побудительную причину (причины), которая (которые) как раз и может быть выявлена с помощью факторного анализа. Существует также техника Р, предполагающая анализ исследований, выполненных на одном и том же индивидууме в различные промежутки времени («объекты» – один и тот же индивидуум в различные промежутки времени), причем изучаются корреляции между состояниями индивидуума. Аналог техники Q для последнего случая составляет предмет исследования техники O.
В основе всех методов факторного анализа лежит предположение, что изучаемая зависимость носит линейный характер. Основное требование к исходным данным – это то, что они должны подчиняться многомерному нормальному распределению. По крайней мере, должно быть сделано допущение о многомерном нормальном распределении совокупности.
Редуцированием корреляционной матрицы называется процесс замены единиц на главной диагонали корреляционной матрицы некоторыми величинами, называемыми общностями. Общность – сумма квадратов факторных нагрузок. Общность данной переменной – та часть ее дисперсии, которая обусловлена общими факторами. Это вытекает из предположения что полная дисперсия складывается из общей дисперсии, обусловленной общими для всех переменных факторами, а также специфичной дисперсии, обусловленной факторами, специфичными только для данной переменной, и дисперсии, обусловленной ошибкой.
Получение матрицы факторного отображения в принципе является целью факторного анализа. Ее строки представляют собой координаты концов векторов, соответствующих т переменным в r -мерном факторном пространстве. Близость концов этих векторов дает представление о взаимной зависимости переменных. Каждый вектор в сжатой, концентрированной форме несет информацию о процессе. Близость этих векторов дает представление о взаимной зависимости переменных. Дополнительно, если число выделенных факторов больше единицы, обычно производится вращение матрицы факторного отображения с целью получения так называемой простой структуры.
Для наглядности результаты можно изобразить графически, что, однако, проблематично для трех и более выделенных факторов. Поэтому обычно дают изображение r -мерного факторного пространства в двумерных срезах.
В процессе решения задачи факторного анализа нужно быть готовы к тому, что иногда решение получить не удается. Это вызвано сложностью решаемой проблемы собственных значений корреляционной матрицы. Например, корреляционная матрица может оказаться вырожденной, что может быть вызвано совпадением или полной линейной корреляцией параметров. Для матриц высоко порядка может произойти потеря значимости в процессе вычислений. Поэтому теоретически нельзя исключить ситуацию, когда методы факторного анализа, к сожалению, окажутся неприменимы, по крайней мере до тех пор, пока исходные данные не удастся «исправить». Исправлены данные могут быть следующим образом. Выявите линейно зависимые параметры с помощью, например, метода и корреляционных плеяд (возможно применение и других методов) и оставьте в исходных данных только один из группы линейно зависимых параметров.
МЕТОД ГЛАВНЫХ КОМПОНЕНТ
С увеличением размерности признакового пространства возрастают трудности изучения геологических объектов, и возникает проблема замены многочисленных наблюдаемых признаков меньшим их числом, без существенной потери полезной информации. Одним из наиболее распространенных методов решения этой задачи является метод главных компонент.
Основой метода главных компонент является линейное преобразование т исходных переменных (признаков) в т новых переменных, где каждая новая переменная представляет собой линейное сочетание исходных. В процессе преобразования векторы наблюдаемых переменных заменяются новыми векторами (главными компонентами), которые вносят резко различные вклады в суммарную дисперсию многомерных признаков. Сокращение пространства признаков достигается путем отбора нескольких наиболее информативных компонент, обеспечивающих основную долю суммарной дисперсии, что приводит к заметному уменьшению их общего числа за счет наименее информативных компонент, отражающих малые доли суммарной дисперсии.
Главные компоненты – это собственные векторы ковариационных матриц исходных признаков. Число собственных векторов ковариационной матрицы определяется числом изучаемых признаков, то есть равно числу ее столбцов (или строк). Каждый собственный вектор (главная компонента) характеризуется собственным значением и координатами.
Собственные значения ковариационной матрицы (λj) – это длины ее собственных векторов, то есть их дисперсии. Суммы собственных значений ковариационной матрицы равны ее следу, то есть сумме ее диагональных элементов.
Координаты собственного вектора ковариационной матрицы (ωij) – это числовые коэффициенты, характеризующие его положение в т мерном признаковом пространстве. Число точечных координат каждого собственного вектора (ωij) – ω 1, ω 2,..., ωm определяется размерностью пространства, а их численные значения – это коэффициенты линейных уравнений данного собственного вектора.
Собственные значения ковариационной матрицы находятся как характеристические корни полиномиальных уравнений путем их решения. Однако осуществить это для больших значений т очень сложно. Поэтому в вычислительной практике их определяют методами матричных преобразований (путем последовательных приближений к собственным значениям), которые могут быть реализованы только с помощью ЭВМ. Методы отыскания координат собственных векторов симметричных матриц также сложны и требуют применения ЭВМ.
Поскольку ковариационные матрицы исходных признаков симметричны, их собственные векторы всегда ортогональны, а составляющие их переменные взаимонезависимы, то есть не коррелированы между собой.
В методе главных компонент координаты собственных векторов рассматриваются как нагрузки соответствующих переменных на тот или иной фактор. Они используются для расчета матриц нового (множества совокупностей путем проектирования векторов исходных данных (признаков х 1, х 2, …, хm) на оси собственных векторов (γ 1, γ 2, …, γm):
, (VII.1)
где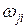 
– нагрузки j -й компоненты в i -й переменной признака. С помощью формулы (VII.1) исходная матрица наблюденных признаков размерности п x т пересчитывается в матрицу новых переменных (той же размерности), учитывающих собственные значения каждой из компонент. Если статистические (корреляционные) связи между наблюденными признаками многомерного пространства проявляются достаточно отчетливо, то разложение исходной матрицы наблюдений на т новых компонент приводит к заметному возрастанию контрастности распределения дисперсий по новым компонентам, в сравнении с исходными векторами. Как правило, дисперсия одной из главных компонент достигает половины и более от суммарной дисперсии признаков, а в совокупности с дисперсиями еще одной-двух последующих компонент, их общий вклад в суммарную дисперсию превышает 90%.
Таким образом, без существенной потери информации об изменчивости наблюденных признаков можно заметно сократить размерность пространства наблюденных признаков (до p ≤ m), ограничившись данными по двум-трем наиболее информативным главным компонентам. Это позволяет считать, что вместо исходной матрицы размерностью п x m, для целей геологического анализа может использоваться матрица главных компонент размерностью п x p (где p, как правило не превышает 2 – 3). Поскольку новые переменные в этой матрице представлены некоррелированными величинами, метод главных компонент может рассматриваться как мощное средство определения истинного числа линейно независимых векторов, содержащихся в исходной матрице.