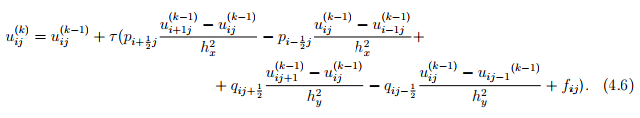Разностные схемы для уравнений эллиптического типа.
Постановка задачи рассмотрим задачу Дирихле для эллиптического уравнения:
– Прямоугольник, а
–Достаточно гладкие функций,
–где 
-постоянные,
Построение сетки, равномерной по каждому из направлений
Разобьем отрезок [0, 
] на N равных частей. Обозначим 
= /N, 
= 
, 0 ≤i ≤ N.
Разобьем отрезок [0, 
] на M равных частей. Обозначим. 
= /N, 
= 
, 0 ≤i ≤ M.
Построим сетку узлов:
Узлы (, ), 1 ≤ i ≤ N - 1; 1 ≤ j ≤ M – 1 - внутренние, остальные, лежащие на границе прямоугольника, — граничные. Внутренний узел (, 
будем называть приграничным,
если хотя бы один из узлов (
, ), (
, ), (
), (
) является граничным.
Приграничные узлы отмечены на рисунке кружочками.
Разностная аппроксимация задачи Дирихле Обозначим 
≈(, Заменяем оператор L во всех внутренних узлах разностным оператором
1 ≤ i ≤ N − 1; 1 ≤ j ≤ M − 1.
Здесь использованы обозначения:
Если u(x, y) имеет не менее четырех непрерывных ограниченных в рассматриваемой
области производных по x и по y, а p(x, y) и q(x, y) — не менее трех, то разностный оператор
аппроксимирует дифференциальный L со вторым порядком, т. е.
Задаче (1.1)-(1.2) ставим в соответствие разностную задачу: найти сеточную функцию,
удовлетворяющуювовнутреннихузлахуравнениям
и принимающую в граничных узлах заданные значения
При достаточной гладкости функций u(x, y), p(x, y), q(x, y) разностная схема (3.2)-(3.3)
имеет второй порядок точности. Для исследования разностного оператора этой задачи
следует в приграничных уравнениях исключить неизвестные 
, 
, 1 ≤j ≤M − 1 и
, 
1 ≤ i ≤ N − 1. Итак, решение задачи (1.1)-(1.2) свелось к решению линейной системы порядка (N − 1) · (M − 1). Линейную систему запишем в виде
где U = (
,..., 
,..., 
,..., 
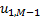, а вектор F отличается от вектора f в (3.2) лишь в приграничных узлах. Отметим следующие особенности матрицы системы A:
• собственныечисламатрицынаходятсявдиапазоне [δ, ∆], где
Заметим, что при p(x, y) ≡ 1, q(x, y) ≡ 1, = = 1, = = h (такую задачу в дальнейшем будем называть простейшей)
• положительную определенность;
• плохую обусловленность, т. е. отношение максимального собственного числа матрицы к минимальному очень велико и является величиной O(1/ 
);
• большой порядок;
• большое количество нулевых элементов;
• специфическую ленточную структуру — блочный трехдиагональный вид
где матрица C является трехдиагональной, I — диагональной, O имеет лишь нулевые элементы. Пусть p(x, y) ≡ 1, q(x, y) ≡ 1, = = h, тогда
Для решения системы могут быть использованы, например, следующие методы:
1. Метод простой итерации.
2. Метод итерации с оптимальным параметром.
3. Метод Зейделя.
4. Метод верхней релаксации.
5. Итерационный метод с оптимальным чебышевским набором параметров.
6. Попеременно треугольный итерационный метод.
7. Итерационный метод переменных направлений.
8. Метод покомпонентного расщепления на основе схемы Кранка-Никольсона.
9. Метод расщепления предиктор-корректор.
10. Метод переменных направлений Дугласа-Рэкфорда.
Метод простой итерации
Систему AU = F сводим к системе вида U = HU + g так, чтобы ρ(H) < 1, где ρ(H) — максимальное по модулю собственное число матрицы H (спектральный радиус матрицы). Пусть H = E − 
A, g = F, где D — диагональная часть матрицы A. В простейшем случае (коэффициенты уравнения постоянные, сетка квадратная) система примет следующий вид:
Расчетная формула метода итерации 
= 
+ g или в простейшем случае поком- понентно имеет следующий вид:
Расчетная формула метода простой итерации в общем случае:
где 1 ≤ i ≤ N − 1; 1 ≤ j ≤ M − 1. Необходимое и достаточное условие сходимости метода ρ(H) < 1 выполнено. Это легко показать в простейшем случае, т. е. при
Обратим внимание, что в простейшем случае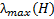 
= 
. Скорость сходимости метода зависит от того, насколько ρ(H) меньше единицы, так как
Здесь 
— точное решение задачи (1.1)-(1.2). Ввиду того, что ρ(H) = 1 − O(), при уменьшении шага сетки h сходимость замедляется, и близость двух соседних приближений (характеристика 5.6 в п.6), часто ошибочно воспринимаемая за признак хорошей точности, говорит лишь о медленной сходимости метода. Известно, что
В общем случае в методе с оптимальным параметром ρ(H) = 
или в обозначении
ξ = 
ρ(H)= 
.
Метод итерации с оптимальным параметром
Как известно, указанному условию сходимости (ρ(H) < 1) будет удовлетворять система вида U = U +τ (F −AU), где τ = 2/(∆+δ), т. е. при H = E −τA, g = τF, τ — оптимальный параметр. Для простейшего случая τ = /4 и система будет иметь следующий вид:
В простейшем случае метод итерации с оптимальным параметром совпадает с методом простой итерации. В общем случае расчетная формула метода итерации с оптимальным параметромимеет вид:
