1. Константу можно выносить за знак дифференциала.
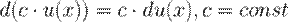
2. Дифференциал суммы/разности.
Дифференциал суммы/разности функций равен сумме/разности дифференциалов от каждого из слагаемых.

3. Дифференциал произведения.
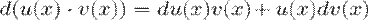
4. Дифференциал частного.

5. Дифференциал константы равен нулю.

Таблица производных и правил дифференцирования основных элементарных и сложных функций:
| Правила дифференцирования | |||
|
| ||
| Формулы дифференцирования | |||
| Основные элементарные функции | Сложные функции | ||
1. 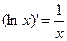 2.
2. 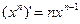 3.
3. 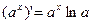 4. (sinx)’=cosx
5.
4. (sinx)’=cosx
5.  6.
6.  7.
7. 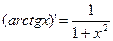
|
8. 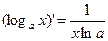 9.
9.  10.
10.  11. (cosx)’= -sinx
12.
11. (cosx)’= -sinx
12. 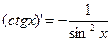 13.
13.  14.
14. 
|
1.  2.
2. 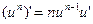 3.
3.  4. (sin u)’=cos u u’
5.
4. (sin u)’=cos u u’
5.  6.
6.  7.
7. 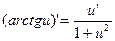
|
8.  9.
9. 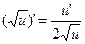 10.
10.  11. (cos u)’= -sin u u’
12.
11. (cos u)’= -sin u u’
12.  13.
13.  14. 14. 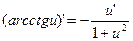
|
Пример
Задание. Найти производную функции 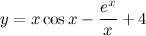
Решение. Используем правила дифференцирования и таблицу производных:

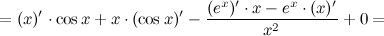

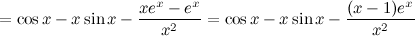
Ответ. 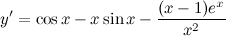
Пример
Задание. Найти производную сложной функции 
Решение. Используем правила дифференцирования и таблицу производных сложных функций:
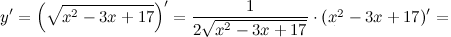

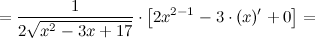

Ответ. 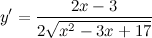
Производная степенно-показательной функции
Степенно-показательной функцией (или показательно-степенной, или функцией в степени функция) называется функция вида 
1-ый способ: Применяя формулу:
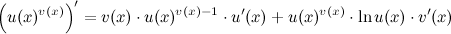
То есть вначале производная берется как от степенной функции, а потом как от показательной.
Замечание
Порядок следования слагаемых неважен: можно вначале взять производную от показательной функции, а затем как от степенной, так как от перестановки слагаемых сумма не меняется:
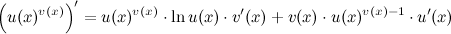
Пример
Задание. Найти производную функции 
Решение. Применяем формулу. В рассматриваемом случае

Тогда имеем:
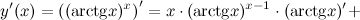
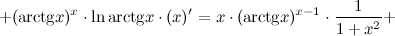
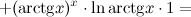


Ответ. 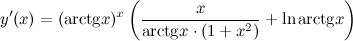
2-ой способ: С помощью логарифмического дифференцирования:

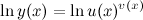





Пример
Задание. Найти производную функции  с помощью логарифмического дифференцирования.
с помощью логарифмического дифференцирования.
Решение. Прологарифмируем левую и правую часть заданной функции, будем иметь:
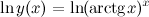
По свойствам логарифмов в правой части полученного равенства степень подлогарифмической функции выносим перед логарифмом:

Дифференцируем левую и правую часть равенства. Слева берем производную как от сложной функции(так как 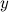 - это функция от переменной
- это функция от переменной  ), а справа - как производную произведения:
), а справа - как производную произведения:
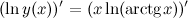
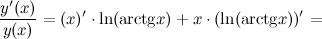
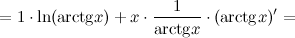
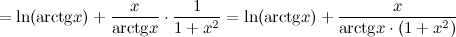
А тогда
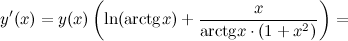

Ответ. 
Монотонность функции и ее связь с производной
Определение
Функция  называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.
называется строго возрастающей на промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции, т.е.
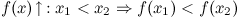
Пример
Функция  является возрастающей на промежутке
является возрастающей на промежутке 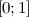 , так как:
, так как:
для 
Определение
Функция  называется строго убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.
называется строго убывающей на промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции, т.е.
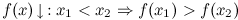
Функция  строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.
строго возрастающая или строго убывающая на промежутке называется монотонной на этом промежутке.
Определение
Функция  называется неубывающей на промежутке, если из неравенства
называется неубывающей на промежутке, если из неравенства 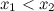 следует неравенство
следует неравенство 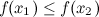 .
.
Функция  называется невозрастающей на промежутке, если из неравенства
называется невозрастающей на промежутке, если из неравенства 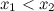 следует неравенство
следует неравенство 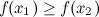 .
.
Связь монотонности функции с ее производной
