Лекция Приложения дифференциального исчисления функции нескольких переменных
Учебные и воспитательные цели: дать системные основы приложения дифференциального исчисления функции нескольких переменных
1. Экстремум функции двух переменных.
2. Необходимые и достаточные условия экстремума.
3. Наибольшее и наименьшее значения функции в замкнутой области.
Экстремум функции двух переменных
Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.
Пусть функция  определена в некоторой области
определена в некоторой области  , точка
, точка  .
.
Точка  называется точкой максимума функции
называется точкой максимума функции  , если существует такая
, если существует такая  - окрестность точки
- окрестность точки  , что для каждой точки
, что для каждой точки 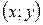 , отличной от
, отличной от  , из этой окрестности выполняется неравенство
, из этой окрестности выполняется неравенство  .
.
Аналогично определяется точка минимума функции: для всех точек 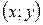 , отличных от
, отличных от  , из
, из  - окрестности точки
- окрестности точки  выполняется неравенство:
выполняется неравенство:  . На рис.
. На рис. 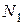 - точка максимума, а
- точка максимума, а  - точка минимума функции
- точка минимума функции  .
.
 |
Необходимые и достаточные условия экстремума
Теорема (необходимые условия экстремума).
Если в точке  дифференцируемая функция
дифференцируемая функция  имеет экстремум, то ее частные производные в этой точке равны нулю:
имеет экстремум, то ее частные производные в этой точке равны нулю: 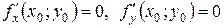 .
.
Точка, в которой частные производные первого порядка функции  равны нулю, т.е.
равны нулю, т.е.  , называется стационарной точкой функции
, называется стационарной точкой функции  .
.
Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называются критическими точками.
В критических точках функция может иметь экстремум, а может и не иметь. Равенство нулю частных производных является необходимым, но не достаточным условием существования экстремума.
Теорема (достаточное условие экстремума).
Пусть в стационарной точке  и некоторой ее окрестности функции
и некоторой ее окрестности функции  имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке
имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке  значения
значения 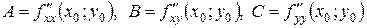 . Обозначим
. Обозначим  .
.
Тогда:
1. если  , то функция
, то функция  в точке
в точке  имеет экстремум: максимум, если
имеет экстремум: максимум, если  ; минимум, если
; минимум, если  ;
;
2. если  , то функция
, то функция  в точке
в точке  экстремума не имеет;
экстремума не имеет;
В случае 
 экстремум в точке
экстремум в точке  может быть, может не быть. Необходимы дополнительные исследования.
может быть, может не быть. Необходимы дополнительные исследования.
Пример.
Найти экстремум функции 
Решение.
 . Точки, в которых частные производные не существуют, отсутствуют.
. Точки, в которых частные производные не существуют, отсутствуют.
Найдем стационарные точки, решая систему уравнений:


Отсюда получаем точки  и
и  .
.
Находим частные производные второго порядка данной функции:  .
.
В точке  имеем:
имеем:  , отсюда
, отсюда  , т.е.
, т.е.  .
.
Т. к.  , то в точке
, то в точке  функция имеет локальный максимум:
функция имеет локальный максимум:

В точке  и, значит,
и, значит,  . Проведем дополнительное исследование. Значит, в окрестности точки
. Проведем дополнительное исследование. Значит, в окрестности точки  функция
функция  принимает как отрицательные, так и положительные значения. Следовательно, в точке
принимает как отрицательные, так и положительные значения. Следовательно, в точке  функция экстремума не имеет.
функция экстремума не имеет.
Наибольшее и наименьшее значения функции в замкнутой области
Пусть функция  определена и непрерывна в ограниченной замкнутой области
определена и непрерывна в ограниченной замкнутой области  Тогда она достигает в некоторых точках
Тогда она достигает в некоторых точках  своего наибольшего
своего наибольшего  и наименьшего
и наименьшего  значений (т.н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области
значений (т.н. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области  , или в точках, лежащих на границе области.
, или в точках, лежащих на границе области.
Правило нахождения наибольшего и наименьшего значений дифференцируемой в области  функции
функции  состоит в следующем:
состоит в следующем:
1. Найти все критические точки функции, вычислить значение функции в них.
2. Найти наибольшее и наименьшее значение функции на границах области.
3. Сравнить все найденные значения функции и выбрать из них наименьшее и наибольшее.
Пример.
Найти наибольшее и наименьшее значения функции  в замкнутой области, ограниченной линиями:
в замкнутой области, ограниченной линиями: 
Решение.

1. Находим все критические точки:  решением системы являются точки
решением системы являются точки  ни одна из точек не принадлежит области
ни одна из точек не принадлежит области 
2.  Исследуем функцию
Исследуем функцию  на границе области, состоящей из участков
на границе области, состоящей из участков 
На участке  , где
, где  ,
,
 . Значения функции
. Значения функции  ,
,
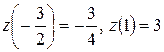 .
.
На участке  , где
, где  . Значения функции
. Значения функции  .
.
На участке 

Значения функции 
3. Сравнивая полученные результаты, имеем:

Правило:
1)  Найти частные производные первого порядка и критические точки
Найти частные производные первого порядка и критические точки

2) Найти частные производные второго порядка и вычислить их значения в критической точке  .
.
3) Используя достаточное условие (Т.2.2) определить знаки  и
и  и сделать вывод о существовании экстремума.
и сделать вывод о существовании экстремума.