1) 
.
2) 
.
3) 
.
4) 
.
5) 
.
6) Оценка определенного интеграла: если 
на 
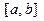, то 
.
7) Если 
четная функция, то 
.
8) Если нечетная функция, то 
.
Пример 2.4.
, поскольку подынтегральная функция – нечетная функция.
Пример 2.5.
, т.к. подынтегральная функция – четная функция.
Замена переменной в определенном интеграле
Если функция непрерывна на отрезке 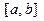, а функция 
непрерывна вместе со своей производной 
на 
, причем 
, то
(19)
Порядок вычисления:
1) ввести новую переменную с помощью подстановки вида 
или 
. Выбор подходящей переменной см. по п. 1.4.1 (табл. 2), п-п. 1.6 и 1.7;
2) продифференцировать введенную в п. 1) подстановку;
3) найти новые пределы интегрирования 
и 
с помощью формулы из п. 1);
4) выразить все, что стоит под знаком интеграла, через новую переменную;
5) вычислить полученный интеграл.
Отметим, что если при вычислении определенного интеграла методом замены переменной аккуратно выполнены п.1)-4), то возвращаться к старой переменной не нужно, а можно вычислить интеграл, используя новую переменную.
Пример 2.6.
. Подынтегральная функция непрерывна в области интегрирования. Применим формулу замены переменной. В табл. 2 находим требуемую подстановку 
, новые пределы интегрирования имеют вид: если 
, то 
, если же 
, то 
. Выразив подынтегральное выражение, вычислим полученный интеграл: 
.
Пример 2.7.
. Подынтегральная функция – четная относительно 
, поэтому по свойству 7 из п. 2.5 получим: 
. Поскольку подынтегральная функция нечетная относительно 
, то подстановка 
приводит к цели (см. табл.4 и 5): 
.
Пример 2.8.
. Подынтегральная функция непрерывна в области интегрирования. Здесь значение интеграла можно вычислить, используя замену 
(см. табл. 2):
. Отметим, что этот результат можно получить и без вычислений, заметив, что подынтегральная функция нечетна относительно , и воспользовавшись свойством 8 из п. 2.5.
Интегрирование по частям в определенном интеграле
Если функции 
и их производные 
непрерывны на отрезке 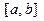, то имеет место формула интегрирования по частям в определенном интеграле:
(20)
Порядок вычисления:
1) все подынтегральное выражение разбить на две части, одну обозначить символом 
, другую -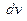 
(см. п. 1.4.2);
2) вычислить дифференциал 
функции и найти функцию 
по ее дифференциалу, интегрируя ;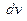
3) применить формулу интегрирования по частям, проверив предварительно непрерывность функций 
.
Формула интегрирования по частям в определенном интеграле применяется для тех же типов интегралов, что описаны в п. 1.4.2.
Пример 2.9.
. Т.к. функции 
непрерывны на 
, то можно использовать формулу интегрирования по частям в определенном интеграле.
Пример 2.10.
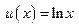. Отметим, что поскольку функции 
и 
непрерывны на 
, формулой интегрирования по частям пользоваться можно.
Несобственные интегралы
Вводя понятие определенного интеграла, мы исходили из условий ограниченной подынтегральной функции и конечности пределов интегрирования. Такой интеграл называют собственным (в данном случае слово «собственный» обычно опускается). Если хотя бы одно из этих условий не выполнено, то интеграл называют несобственным. Т. е. несобственный интеграл от непрерывной функции, но с бесконечным промежутком интегрирования (несобственный интеграл I рода) или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющей на нем бесконечный разрыв (несобственный интеграл II рода).