Проблема разрешимости.
Все формулы алгебры логики делятся на тождественно истинные, тождественно ложные и выполнимые. Определения тождественно истинных и тождественно ложных формул даны выше.
Формулу F называют ВЫПОЛНИМОЙ, если она принимает значение “истина” (1) хотя бы на одном наборе значений входящих в неё переменных и не является тождественно истинной.
В связи с этим возникает задача получения ответа на вопрос: к какому классу относится данная формула?
Эта задача называется ПРОБЛЕМОЙ РАЗРЕШИМОСТИ.
Очевидно, что проблема разрешимости алгебры логики разрешима.
Действительно, для каждой формулы алгебры логики может быть составлена таблица истинности, которая и даст ответ на поставленный вопрос. Однако практическое использование таблиц истинности при большом количестве переменных 
затруднительно.
Существует другой способ, позволяющий, не используя таблицы истинности, определить, к какому классу относится формула F. Этот способ основан на приведении формулы к нормальной форме (ДНФ или КНФ) и использовании алгоритма, который позволяет определить, является ли рассматриваемая формула тождественно истинной или не является. Одновременно с этим решается вопрос о том, будет ли формула A выполнимой.
Предположим, что мы имеем критерий тождественной истинности для формул алгебры логики. Рассмотрим механизм его применения.
Применим критерий тождественной истинности к формуле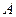 
. Если окажется, что формула 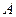– тождественно истинная, то задача решена. Если же окажется, что формула 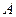не тождественно истинна, то применим критерий тождественной истинности к формуле 
. Если окажется, что формула - тождественно истинная, то ясно, что формула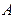 
- тождественно ложная, и задача решена. Если же формула не тождественно истинная, то остаётся единственный возможный результат: формула 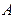выполнима.
Установим теперь критерий тождественной истинности произвольной формулы алгебры логики. С этой целью предварительно сформулируем и докажем критерий тождественной истинности элементарной дизъюнкции.
Теорема 1.
Для того, чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно, чтобы в ней содержалась переменная и её отрицание.
Доказательство необходимости.
Пусть элементарная дизъюнкция тождественно истинна, но в неё одновременно не входит некоторая переменная и её отрицание. Придадим каждой переменной, входящей в элементарную дизъюнкцию без знака отрицания, значение “ложь”, а каждой переменной, входящей в элементарную дизъюнкцию под знаком отрицания - значение “истина”. Тогда, очевидно, вся элементарная дизъюнкция примет значение “ложь”, что противоречит условию.
Доказательство достаточности.
Пусть теперь элементарная дизъюнкция содержит переменную и её отрицание. Так как 
, то и вся элементарная дизъюнкция будет тождественно истинной.
Критерий тождественной истинности элементарной дизъюнкции позволяет сформулировать и доказать критерий тождественной истинности произвольной формулы алгебры логики.
Теорема 2.
Для того, чтобы формула алгебры логики 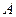была тождественно истинна, необходимо и достаточно, чтобы любая элементарная дизъюнкция, входящая в КНФ 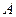, содержала переменную и её отрицание.
Доказательство необходимости.
Пусть 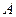- тождественно истинна. Тогда и КНФ 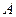- тождественно истинна.
Но КНФ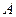 
, где 
- элементарные дизъюнкции (
).
Так как КНФ 
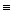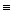1, то 1, . Но тогда по теореме 1 каждая элементарная дизъюнкция содержит переменную и её отрицание.
Доказательство достаточности.
Пусть любая элементарная дизъюнкция , входящая в КНФ 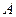, содержит переменную и её отрицание. Тогда по теореме 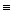1 1, .
При этом и КНФ 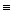1.
Например, выясним, является ли формула 
тождественно истинной.
Так как 
, то ясно, что каждая элементарная дизъюнкция 
и 
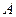, входящая в КНФ , содержит переменную и её отрицание. Следовательно, 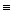1.
Аналогично имеют место теоремы, дающие критерии тождественной ложности элементарной конъюнкции и любой формулы алгебры логики.
Теорема 3.
Для того, чтобы элементарная конъюнкция была тождественно ложной, необходимо и достаточно, чтобы в ней содержалась переменная и её отрицание.
Теорема 4.
Для того, чтобы формула алгебры логики была тождественно ложной, необходимо и достаточно, чтобы любая конъюнкция, входящая в ДНФ , содержала переменную и её отрицание.
Рассмотрим некоторые приложения алгебры логики.