Угол между прямыми в пространстве

11.

12. Метод Гаусса.

Сначала следует привести систему к треугольному (ступенчатому) виду, а затем ступенчато решить.

Формула Крамера.

Подсчитать определитель матрицы А.

Затем матрицей B заменить первый столбец матрицы А, подсчитать определитель и разделить его на detA, так мы получим x₁. То же самое проделать со 2-ым и 3-им столбцом.

13. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Найти какой-либо базисный минор порядка r. Взять r уравнений, из которых составлен базисный минор. Неизвестные, коэффициенты которых входят в базисный минор, называются главными и остаются слева, а остальные называются свободными и переносятся в правую часть уравнения. Найдя главные через свободные, получим общее решение системы.

14. теорема1:если ранг матрицы совместной системы=чису неизвестных,то система имеет 1 решение. Теорема2: Если ранг матрицы совместной системы < числа неизвестных,то множество решений системы бесконечно. Теорема3:Если система имеет 1 решение,то ранг матрицы системы=числу неизвестных. Теорема4: Если множество решений системы бесконечно,то ранг > числа.

Правило решения:1.находим r_a и r_a, если r_a не равен r_a, то система не соместна(нет решений). 2. Если r_a = r_a = r, то система совместа.Выделяем базисный минор и базисные неивестные.3.Эту систему заменяем равносильной,состоящей из тех r- уравнений, в кот. вошли элементы базисного минора.4.Если число базисн.неизвестн.=числу неизвестн.то система имеет 1 решение,кот. можно найти по формуле крамера.5. Если число базисн. Неизвестных < числа неизв.системы,то из системы пункта 3 находим выражение базисн.неизвестных через свободные.Используя формулы Кррамера.Придавая свободным неизвестным произвольные значения получим бесконечное множество решений.

15. Система однородных уравнений всегда имеет нулевое решение. Если ранг матрицы меньше числа неизвестных, то система имеет бесчисленное множество решений. Для того, чтобы система имела ненулевые решения, необходимо, чтобы ее определитель был равен нулю.

19. Если какой-то из векторов системы явл. линейной комбинацией др.вектора то все эти вектора будут линейно-зависимы.любые 2 колиниарные вектора линейно зависимы. Все 3 вектора a, b, с на плоскости линейно-зависимы.1 из комплонарных векторов явл. линейной комбинацией оставшихся. Все 4 вектора в пространстве a, b, с, d линейно-зависимы.

20. теорема1. любые 2 коллиниарные вектора линейно зависимы. 2 неколлиниарных вектора независимы. По определению коллиниарности векторов следует что b=λa;тогда λa-b=0

Теорема2. Все 3 вектора a, b, с на плоскости линейно-зависимы. 3 некомплонарных вектора линейно-независимы. 1 из комплонарных векторов явл. линейной комбинацией оставшихся. Возможны 2 случая: среди комплонарных векторов есть пара коллиниарных векторов а, b a=λb, тогда a= λb+0c; и когда среди векторов нет пары коллиниарных.

Теорема3. Все 4 вектора в пространстве a, b, с, d линейно-зависимы. таким образом показано что любой вектор d в пространстве может быть как линейная операция d=αa+βb+γс

21. Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.

Базисом в пространстве наз. совокупность фиксированной точки в пространстве и 3х некомпланарных векторов.

 

Любой вектор на плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в пространстве может быть разложен по векторам базиса в пространстве.

ОС = OA + OB, OA =x* i, OB =j*y, OC =x i +y j. Числа х,у наз-ся координатами вектора ОС в данном базисе

 

 

Таким образом базис позволяет вектору а поставить в соответствие тройку чисел(α,β,γ). Для плоскости двойку чисел.

22. эта система определяется тройкой взаимно-ортогональных и единичных базисных векторов.Этот базис наз.ортонормарованным. Систему этих векторов будем обозначать в пространстве(I,j,k)

23. в прямоугольно-декартовой системе координат, координаты вектора соотв. Проекциям вектора на оси координат. αβγ – углы кот.образует вектор с осями координат соответственно.

Cosα, cosβ, cosγ – направляющие cos вектора.

24. формулы деления отрезка в заданном отношении. Если делить отрезок пополам,то в знаменателе будет 2

25. (“skala”-шкала) 2х векторов а и в наз. число, равное произведению длин этих векторов на cos угла между ними. (а, в)- скалярное произведение. а * в =| а |*| в |*cosj, j=p/2, cosp/2=0, a^b=> ab =0. Равенство “0” скаляргного произведения необходимое и достаточное условие их перпендикулярности (ортогональности).

26. (a,b)=x₁x₂+y₁y₂+z₁z₂

27.

левая ----- правая

Тройка векторов а, в, с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки - левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям: 1. | c |=| a |*| b |*sinj. 2. c ^ a и c ^ b. 3. тройка а, в, с -правая.

28.

29. Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a * b * c =[ a * b ]* c = a *[ b * c ], где

a ={a_x,a_y,a_z}

b ={b_x,b_y,b_z}

c ={c_x,c_y,c_z}

Св-ва:
1. При перестановке 2х сомножителей:

a * b * c =- b * c * a

2. не меняется при перестановке циклических сомножителей:

a * b * c = c * a * b = b * c * a

3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a * b * c =0

б)если некомпланарные вектора a, b, c привести к 1 началу, то | a * b * c |=Vпараллепипеда, построенного на этих векторах

если a * b * c >0, то тройка a, b, c - правая

если a * b * c <0, то тройка a, b, c - левая

30. вектор а= (x₁, y₁, z₁) вектор b= (x₂, y₂, z₂) вектор c=(x₃, y₃, z₃)

31. каждой паречисел на плоскости соответствует точка.Это соответствие позволяет свести изучение геометрических образов к изучению алгебраич. соотношений, во многих случаях это упрощает решение задач.

Ф(х,у)=0 наз. уравнением линии (L), ecли этому уравнению удовлетворяют координаты (х,у) любой точки лежащей на линии (L), и не удовлетворяет координ. (х,у) ни одной точки не лежащей на (L).

Ф(х,у)=0 – определяет линию на плоскости.

32. Часто удобно задавать линию не только Ф(х,у)=0, а системой уравнений, в кот. х, у задаются как функции t, кот. наз. параметром.

(х=ᴪ(t), y=µ(t)) параметрические уравнения линий. При изменении t меняется х, у и точка перемещается по линии.

33. x, y, z –координаты текущей точки в поверхности, тогда придем к уравнению Ф(x, y, z)=0. – уравнение поверхности S, если ему удовлетворяет координаты x, y, z любой точки лежащей на поверхности и не удовлетвор. координ. x, y, z не одной точки не лежащей на поверхности.Всякую линию в пространстве мы можем рассматривать как линию пресечения двух поверхностей. Линия в пространстве может быть задана параметрическим уравнением. (х=x(t); y=y(t); z=z(t))

34. Пусть плоскость задана точкой M₀(x₀;y₀;z₀) и вектором , перпендикулярной этой плоскости.

Возьмем произвольную точку M(x;y;z) и составим вектор 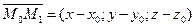. При любом расположении точки М на плоскости Q , поэтому .

Общее уравнение плоскости.

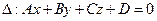
· Если D=0, то данному уравнению удовлетворяет точка О (0;0;0)

· Если С=0 то вектор . Следовательно, плоскость параллельна оси oz, если В=0 – то oy, если А=0 – то ox.

· Если C=D=0, то плоскость проходит через О (0;0;0), параллельно оси oz. Аналогично при A=D=0 и B=D=0.

· Если А=В=0 то уравнение примет вид плоскость параллельна плоскости Oxy.

· Если A=B=D=0, то уравнение имеет вид . Это уравнение плоскости Oxy.

35. Ax+By+Сz-Ax₀-By₀-Сz₀=0

-Ax₀-By₀-Сz₀=D, где D=Ax+By+Сz

Ax+By+Сz+D=0

Частный случай:

Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)

Если A=0, то By+Сz+D=0

Если B=0, то Ax +Сz+D=0

Если C=0, то Ax+By+D=0

Если A=B=0, то Сz+D=0

Если A=C=0, то By+D=0

Если A=D=0, то By+Сz=0

Если B=D=0, то Ay+Сz=0

36. Ax+By+Сz+D=0

1. пусть D=0

Точка (0,0,0) явл. решением. Плоскость проходит через начало координат.

2. Если C=0, то Ax+By+D=0 уравнение определяет плоскость параллельную оси OZ

3. By+Сz=0; Ax +Сz=0; Ax+By=0 (плоскость проходит через ось OX, OY, OZ)

4. B=0, C=0 Ax+D=0; By+D=0; Cz+D=0

5. Ax=0(x=0); By=0(y=0); Cz=0(z=0) находится в плоскости.

37. Уравнение плоскости в отрезках.

Пусть плоскость отсекает на осях отрезки, т.е. проходит через точки:

; ;

 

38. Нормальное уравнение плоскости в координатной форме.

39. Уравнение плоскости, проходящей через три точки

К (х₁;у₁) М (х₂;у₂) N (x₃;y₃)

Возьмем на плоскости точку P (x;y;z).

Составим векторы:

Эти векторы лежат в одной плоскости, следовательно они компланарны:

40.

=0 условие перпендикулярности двух плоскостей.

условие параллельности двух плоскостей.

41. Дано:

M₀ (x₀;y₀;z₀)

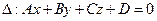
Расстояние d от точки М₀ до плоскости ∆ равно модулю проекции вектора (где М₁(x₁;y₁;z­₁) - произвольная точка плоскости) на направление нормального вектора

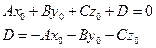
!!!Если плоскость задана уравнением:

то расстояние до плоскости находится по формуле:

42. Уравнение с угловым коэффициентом.

k= tg α – угловой коэффициент.

Если b=0 то прямая проходит через начало координат. Уравнение примет вид

Если α=0, то k = tg α = 0. То прямая пройдет параллельно оси ох.

Если α=π/2, то уравнение теряет смысл. В этом случае уравнение примет вид и пройдет параллельно оси оу.

Общее уравнение прямой.

A, B, C – произвольные числа, причем А и В не равны нулю одновременно.

· Если В=0, то уравнение имеет вид или 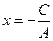. Это уравнение прямой, параллельной оси оу. и проходящей через точку

· Если В≠0, то получаем уравнение с угловым коэффициентом .

· Если А=0, то уравнение имеет вид . Это уравнение прямой, параллельной оси ох.

· Если С=0, то уравнение проходит через т. О (0;0).

Уравнение прямой, проходящей через точку, в данном направлении.

т М (х₀;у₀).

Уравнение прямой записывается в виде .

Подставим в это уравнение точку М

Решим систему:

Уравнение прямой, проходящей через 2 точки.

К (х₁;у₁) М (х₂;у₂)

Уравнение прямой в отрезках.

К (а;0); М (0;b)

Подставим точки в уравнение прямой:

Уравнение прямой, проходящей через данную точку, перпендикулярно данному вектору.

М₀ (х₀;у₀).

Возьмем произвольную точку М (х;у).

Т.к. , то

Нормальное уравнение прямой.

Уравнение прямой можно записать в виде:

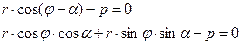
Т.к. ; , то:

 

43.

Дано: прямые L₁ и L₂ с угловыми коэффициентами

Требуется найти угол между прямыми:

 

44. k₂ =k₁ условие параллельности прямых.

k₂ = -1\ k₁ условие перпендикулярности прямых

45.

46. Векторное уравнение прямой.

Положение прямой можно задать по точке и направляющему вектору.

Пусть прямая L задана ее точкой M₀(x₀;y₀;z₀) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z). Обозначим радиус-векторы точек M и M₀ через r и r₀.

Тогда уравнение прямой запишется в виде:

где t – скалярный множитель (параметр).

Параметрические уравнения прямой.

Канонические уравнения прямой.

S(m;n;p) – направляющий вектор прямой L. M₀(x₀;y₀;z₀) – точка на прямой. соединяет M₀ с произвольной точкой М.

47. Общее уравнение прямой.

Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:

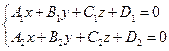
Т.к. прямая перпендикулярна векторам n₁ и n₂ то направляющий вектор запишется как векторное произведение:

48. Уравнение прямой в пространстве, проходящей через две точки.

M₁(x₁;y₁;z₁) M₂(x₂;y₂;z₂)

В качестве направляющего вектора можно задать вектор

Следовательно:

, тогда

Угол между прямыми в пространстве

;

 

условие параллельности двух прямых в пространстве

=0 условие перпендикулярности прямых в пространстве

50. Угол между прямой и плоскостью.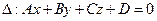

Прямая L:

Пусть φ – угол между плоскостью и прямой.

Тогда θ – угол между и .

Найдем , если

=0 условие параллельности прямой и плоскости.

условие перпендикулярности прямой и плоскости

51,52. возможны 3 случая:

1. Если не равно 0 (прямая и плоскость не параллельны,то находим

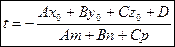
2. =0(прямая параллельна плоскости) не равно 0(точки пересечения нет)

3. =0; =0 прямая лежит на плоскости.

53. Ax²+2Bxy+Cy²+2Dx+2Ey+F=0, где

Окружность (x-a)²+(y-b)²=R²

(a, b) – центр окружности

Если а=0, b=0, то x²+y²=R²

54. Эллипсом называется

геометрическое место всех

точек плоскости, сумма

расстояний от которых до

до фокусов есть величина

постоянная, большая, чем расстояние между фокусами.

Пусть М (х;у) – произвольная точка эллипса.

Т.к. MF₁ + MF₂ = 2a

Т.к.

То получаем

Или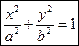

56. Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до фокусов есть величина постоянная.

Пусть M(x;y) – произвольная точка гиперболы. Тогда согласно определению гиперболы |MF₁ – MF₂|=2a или MF₁ – MF₂=±2a,

 

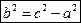
58. Парабола – множество всех точек плоскости, каждая из которых одинаково удалена от фокуса, и директрисы. Расстояние между фокусом и директрисой называется параметром параболы и обозначается через р>0.

Пусть M(x;y) – произвольная

точка M с F. Проведем отрезок

MN перпендикулярно

директрисе. Согласно

определению MF=MN.

60. Уравнение вида Ax²+Cy²+2Dx+2Ey+F=0 всегда определяет либо окружность (при А=С), либо эллипс (при А*С>0), либо гиперболу (при А*С<0), либо параболу (при А*С=0), при этом возможны случаи вырождения: для эллипса (окружности) – в точку или мнимый эллипс (окружность), для гиперболы – в пару пересекающихся прямых, для параболы – в пару параллельных прямых.

Общее уравнение второй степени с двумя неизвестными: Ax²+2Bxy+Cy²+2Dx+2Ey+F=0

Коэффициент В с произведением координат преобразовывает уравнение путем поворота координатных осей.

 

61. Поверхность, образованная вращением некоторой плоской кривой вокруг оси, лежащей в ее плоскости, называется поверхностью вращения. Пусть некоторая кривая L лежит в плоскости Oyz. Уравнение этой кривой запишутся в виде:

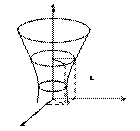Найдем уравнение поверхности, образованной вращением кривой L вокруг оси Oz.

Возьмем на поверхности точку

M (x;y;z). Проведем через точку

М плоскость, перпендикулярную

оси oz, и обозначим точки

пересечения ее с осью oz

и кривой L соответственно O₁ и N.

Обозначим координаты точки

N (0;y₁;z₁). Отрезки O₁M и O₁N

являются радиусами одной и той же окружности. Поэтому O₁M = O₁N. Но O₁M = (x²+y²)^0.5, O₁N=|y₁|.

Следовательно, |y₁|=(x²+y²)^0.5 или y₁=±(x²+y²)^0.5. Кроме того, очевидно, z₁=z.

Следовательно – искомое уравнение поверхности вращения, ему удовлетворяют координаты любой точка М этой поверхности и не удовлетворяет координаты точек, не лежащих на поверхности вращения.

(x-x₀)²+(y-y₀)²+(z-z₀)²=R² кононическое уравнение сферы.

 

62. Конус.

Поверхность, образованная прямыми линиями, проходящими через данную точку Р и пересекающими данную плоскую линию L (не проходящую через Р) называется конической поверхностью или конусом. При этом линия L называется направляющей конуса, точка Р – ее вершиной, а прямая, описывающая поверхность, называется образующей.

- уравнение конуса

Цилиндр.

Поверхность, образованная движением прямой L, которая перемещается в пространстве, сохраняя постоянное направление и пересекая каждый раз некоторую кривую К, называется цилиндром. При этом кривая К называется направляющей цилиндра, а прямая L – образующая.

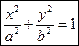- уравнение цилиндра

 

63.

1. Эллипсоид.

2. Однополостный гиперболоид.

3. Двуполостный гиперболоид.

4. Эллиптический.

5. Гиперболический.

6. Конус