Симплекс-метод в решении задач линейного программирования

Графический метод в решении задач линейного программирования

1. Теоретические сведения

Графический метод основан на геометрической интерпретации задачи ЛП и применяется в основном при решении задач в двумерном пространстве.

Необходимо найти вектор , который удовлетворяет системе ограничений и минимизирует функцию Z.

Каждое неравенство определяет в плоскости Х₁0Х₂ полуплоскость с граничной прямой . Точки, лежащие в полуплоскости, удовлетворяют данному неравенству.

Тривиальные неравенства определяют первый квадрат в системе координат.

Множество точек пересечения всех этих полуплоскостей образуют многоугольник решений (область допустимых решений ОДР).

Каждая точка этого многоугольника есть решение системы ограничений (допустимый план задачи ЛП).

Многоугольник решений может быть и неограничен областью или выражаться в прямую, луч, отрезок или вообще в точку.

Если ОДР пустая, то система ограничений несовместна.

Графическое решение задачи ЛП начинают с построения многоугольника решений.

При фиксированном Z=Z₀ равенство представляет собой уравнение прямой, называемой линией уровня, для всех точек которой функция принимает одно и тоже значение .

Если перемещать эту прямую в направлении вектора

это выражение называется антиградиентом, которое показывает направление убывания функции.

Антиградиент всегда должен быть перпендикулярен линии уровня.

Далее будем перемещать линию уровня до тех пор, пока она не окажется в таком положении, что все точки многоугольника решений будут лежать по одну её сторону, или хотя бы одна точка будет лежать на этой прямой.

Таких положений может быть не более двух. Одно из них соответственно min, а другое max.

Соответствующая точка называется оптимальным планом и является решением задачи ЛП.

Если же ОДР не замкнута, то одно или оба этих положений могут отсутствовать.

Очевидно, что прямая проходит хотя бы через одну условную точку многоугольника решений, поэтому оптимальному плану соответствует хотя бы одна условная точка.

Линия уровня может совпадать со стороной многоугольника решений, в этом случае оптимальное решение не единственно (альтернативный оптимум) – оптимальными планами являются обе условные точки и все точки отрезка между ними (∞). Значение функции во всех точках альтернативного оптимума будет одно и тоже.

Характерные черты ЛП:

1. Допустимая область всегда является выпуклым множеством, даже в том случае, когда она ограничена.

2. Оптимальное решение всегда достигается в вершине допустимой области.

3. Если оптимальное решение не одно, то значение функции совпадает во всех точках решения.

 

2. Пример решения задачи ЛП графическим методом

 

 

Симплекс-метод в решении задач линейного программирования

1. Теоретические сведения

Симплексное преобразование.

В основе симплекс-метода лежит идея поиска базисного решения с последующим переходом от одного базиса и другому таким образом, чтобы целевая функция все время увеличивается, если речь идет о задаче максимизации.

Пусть имеем задачу Линейного Программирования канонической форме:

Матрица ограничений имеет вид:

 

_{; ; …;}

 

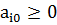
_{Применим метод} полного исключения к расширенной матрице ограничений

1) выбираем направляющий элемент Ai,j на данной итерации, в результате преобразования Гаусса, получим новые значения коэффициентов.

Преобразование Гаусса называется симплексным преобразованием когда направляющий элемент определяется по следующим правилам:

1) Направляющий столбец выбирают из условия, что в нем имеется хотя бы один положительные элемент

2) Направляющую строку выбирают так, чтобы отношение

Задача линейного программирования с помощью симплекс метода, основывается на представлении решения в табличной форме.

Пусть имеется линейная форма

С₁х₁+с₂х₂+…+c_nx_n max

И ограничения даны в следующей форме

a₁₁x₁+a₁₂x₂+…+a_1nx_n a₁₀

a₂₁x₁+a₂₂x₂+…+a_2nx_n a₂₀

_{_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _}

A_m1x₁+a_m2x₂+…+a_mnx_n a_m0

Приведем к каноническому виду

 

Далее составим симплексную таблицу:

С

С1

С2

С3

…

Сj

…

Cn

Bx

A0

A1

A2

A3

…

Aj

…

A11

An+1

…

An+m

Cn+1

Xn+1

a10

a11

a12

a13

…

a1j

…

a1n

…

Cn+2

Xn+2

a20

a21

a22

a23

…

a2j

…

a2n

…

…

…

…

…

…

…

…

…

…

…

…

…

…

Cn+i

Xn+i

ai0

ai1

ai2

ai3

…

aij

…

ain

…

…

…

…

…

…

…

…

…

…

…

…

…

…

Cn+m

Xn+m

am0

am1

am2

am3

…

amj

…

amn

…

a00

a01

a02

a03

…

a0j

…

a0n

ao,n+1

…

a0,n+m

 

a_0k (k= ) – индексная строка, элементы вычисляются следующим образом:

a_0k = =C_n+i-C_k

i – номер строки, т.к. на 1 шаге заполнения таблицы, все C_n+I = 0, то элементам индексной строки присваиваются значения соответствующих элементов данного столбца, взятых с обратным знаком, то есть

a_0k = - C_k индексная строка изучает для определения направляющего столбца

a₀₀ = Σ C_n+k * a_k0 , k – номер базисной переменной

Индексация идет по строкам таблицы. В столбце В_х записываются базисные переменные на 1 шаге в качестве базисных выбирают фиктивные переменные

{X _n+n}, (K= ) в дальнейшем их нужно вывести из базиса

В столбец с записанным коэффициентом при X_n+k на первом шаге значения этих коэффициентов равны 0.

Для перехода от базиса фиктивных переменных и базису реальных.

В качестве направляющего столбца выбирают a_j, для которого выполняется условие a_0j = min {a_0l}, (l= ), при a_0l < 0

 

Выбирают направленную строку, для чего каждый элемент столбца свободных членов делится на соответствующий элемент направленного столбца.

Элемент столбца свободных членов находится в одной строке с элементом направленного столбца

=min

Из всех возможных соотношений выбирается min, при a_rj>0, (r= )

Применяя эти правила, определяем направляющий элемент. Далее выполняется шаг симплексных преобразований. Переменная, которая соответствует направляющему столбцу вводится в базис, а переменная, соответствующая направляющей строке выводится из базиса.

При этом для переменной вводимой в базис, изменяется соотношение значения коэффициентов целевой функции.

a_ij направляющий элемент, то переход от данной таблицы к следующей осуществляется с помощью следующего правила:

а) A_il ^(k+1)= , k=1,2…

i - номер направляющей строки

j – номер направляющего столбца

l=

То есть все элементы направляющей строки делим на направляющий элемент.

В итоге направляющий элемент:

A_ij ^(k+1) =1

 

б) В направляющем столбце нужно получить

a_rj^(k+1)=0, r= r≠i,при a_ij ^(k+1)=1,то есть в направляющем столбце должны быть все 0,кроме направляющего элемента, который равен 1.

Для всех остальных элементов, включая индексную строку проводим следую

следующие вычисления:

a_rl ^(k+1)= a_rl ^(k) – , l , r i

Симплексное преобразование повторяют до тех пор, пока не реализуется один из двух возможных исходов.

А) Все a_0l ≥ 0 – это условие оптимального базиса последней таблицы.

Б) Найдется элемент a0i<0, при котором все элементы столбца a_rj≤0.

Это признак неограниченной целевой функции на множестве допустимых решений.

 

 

2. Пример решения задачи ЛП Симплекс-методом

Дано:

2x₁ + 3x₂ → max
5x₁ + 2x₂ ≤ 18
x₁ + 2x₂ ≤ 10
4x₁ + 5x₂ ≤ 20

Решение:

Приводим ЗЛП к каноническому виду:

2x₁ + 3x₂ → max
5x₁ + 2x₂ + x₃ = 18
x₁ + 2x₂ + x₄ = 10
4x₁ + 5x₂ + x₅ = 20

базисные переменные	x1	x2	x3	x4	x5	свободные члены
x3
x4
x5
z	-2	-3

За ключевой выберем столбец 2, так как -3 максимальный по модулю отрицательный элемент в строке z.

За ключевую выберем строку 3, так как отношение свободного члена к соответствующему элементу ключевого столбца для 3 строки является наименьшим.

5 - разрешающий элемент.

базисные переменные	x1	x2	x3	x4	x5	свободные члены	отношение
x3
x4
x5
z	-2	-3					-

Разделим элементы ключевой строки на разрешающий элемент.

От элементов строки 1 отнимаем соответствующие элементы ключевой строки, умноженные на 2.

От элементов строки 2 отнимаем соответствующие элементы ключевой строки, умноженные на 2.

От элементов строки 4 отнимаем соответствующие элементы ключевой строки, умноженные на -3.

базисные переменные	x1	x2	x3	x4	x5	свободные члены
x3	3.4				-0.4
x4	-0.6				-0.4
x2	0.8				0.2
z	0.4				0.6

Т.к. среди элементов z строки (за исключением элемента столбца свободных членов) нет отрицательных, найдено оптимальное решение.

Ответ:

X_опт = (0; 4; 10; 2; 0)
z_опт = 12

 

Транспортная задача

1. Теоретические сведения