Постановка задачи и стратегия решения.

Предположим, что в пункте А₁, А₂,..,А_n хранится однородный груз в количестве а₁, а₂,..,а_m единиц. Этот груз следует доставить в n заданных пунктов назначения В₁, В₂,..,В_n, причем в каждый из них требуется завезти b₁,b₂,..,b_m единиц этого груза.

Обозначим C_ij стоимость перевозки груза из пункта A_i в пункт B_j.

Транспортные задачи делятся на 2 группы:

1) Задачи, удовлетворяющие условию баланса (закрытая транспортная задача):

_I = _j

Это означает, что общий запас груза на всех пунктах хранения равен суммарной потребности всех пунктов потребления (назначения).

 

2) Задачи с нарушенным балансом (открытая транспортная задача). Среди них выделяют 2 случая:

 

а) _I > _j

 

б) _I < _j

 

Рассмотрим формализацию закрытой транспортной задачи.

Обозначим x_ij количество груза, перевозимого из A_i в B_j. Тогда суммарная стоимость перевозок имеет вид:

ƒ(x) = c_ij x_ij

Ограничения представляются уравнениями вывоза и привоза груза

Первое уравнение системы означает, что из каждого пункта а_i вывозится весь груз А.

Второе уравнение системы означает, что удовлетворяются все потребности b_j.

Третье уравнение системы – груз либо вывозится, либо нет.

Решение x_ij этой системы называют планом перевозки.

1. Метода нахождения начального плана перевозок.

Клетки матрицы перевозок, где x_ij>0 называются базисными клетками. Остальные, где x_ij=0 называются свободными клетками. В матрице перевозок имеется (m+n-1) базисных клеток. Их число совпадает с числом независимых уравнений-ограничений.

Значение x_ij в матрице перевозок находится по формуле:

x_ij = min (*)

Значение x_ij=0 в свободной клетке не пишется явно, а вместо этого в ней ставится прочерк.

· Метод северо-западного угла

Вычисления осуществляются по формуле:

x_ij = min , начиная с элемента x₁₁ стоящего в северо-западном углу матрицы перевозок.

· Метод наименьшей (min) стоимости

Получаемы методом северо-западного угла, начальный план не зависит от стоимости и поэтому, в общем случае, далек от наилучшего. В методе минимальной стоимости учитываются затраты на перевозку.

По формуле (*) последовательно заполняются клетки с наименьшей стоимостью перевозок. Если имеются несколько клеток с наименьшей стоимостью, то из них выбирается любая.

· Метод потенциалов:

Метод обеспечивает улучшения начального плана перевозок при этом происходит переход от одной матрицы к другой до тех пор пока уменьшение суммарной стоимости перевозок станет не возможной.

Введем:

1)Цикл – замкнутая ломанная с вершинами расположенными в оль строк и столбцов матрицы перевозок.

В каждой вершине встречаются два звена причем одно из них располагается по строке а другое по столбцу.

Число вершин цикла всегда четно.

Цикл может само пересекаться- ломаная, но точки само пресечения не могут быть вершинами цикла.

2)Означенный цикл – это цикл в котором некоторой вершине приписан знак «+», а затем при обходе цикла в каком-либо направлении знаки чередуются.

3) сдвиг по циклу на число θ (тета) >= 0, при этом значении X_ij стоящие в положительной вершине цикла увеличивается на число θ, а стоящие в отрицательной вершине уменьшается на θ.

4) Потенциал – это число (α_i, i= 1,m)(β_j,j=1,m) каждому свободному пункту хранения a_i ставиться в соответствие α_i, а пункту потребления в соответствии β_j.

· Алгоритм:

1)Найти начальный план любым методом.

2)Для каждой базисной клетки составить уравнение α_i+β_j = c_ij

Т.к. эти уравнения образуют систему n+m -1 уравнении с m+n неизвестными.(Она имеет бесконечное множество решении)то для определенности следует предположить что α₁= 0, следует все остальные потенциалы находятся однозначно.

3) Для каждой свободной клетки вычислить оценки по следующей формуле Δ_ij= c_ij- α_i-β_j

4) Проанализировать относительные оценки:

а)если все относительные оценки отрицательны т.е. Δ_ij = 0, то задача решена и следует выписать полученный план из матрицы и подсчитать его стоимость.

б)если есть Δ_ij<0 найти среди них наименьшее отрицательную оценку и отметить ее каким-нибудь знаком.

5)для свободной клетки с выбранной оценкой Δ_ij (X)построить означенный цикл, все его вершины кроме 1-ой (X) должны находиться в базисных клетках.

Свободная клетка берется со знаком (+).

6) Выполнить сдвиг по построенному на шаге 5 циклу на величину θ равную наименьшей из чисел, стоящих в положительных вершинах, при этом числа стоящие в отрицательных вершинах уменьшить на θ, а в положительных увеличить на θ.

Если наименьшее значение θ достигается в нескольких отрицательных вершинах цикла то при сдвиге следует поставить базисный 0 во всех кроме одной.

Иногда число базисных клеток сохраняется и будет равно n+m-1 что необходимо проверять при расчетах!

Элементы матрицы не ходящие в цикл остаются без изменении.

Перейти к шагу 2.

· Замечание:

 

1)При решении задач может возникнуть ситуация в которой θ тогда при сдвиге свободная клетка становиться базисной(точка заменяется на базисный 0(ноль))

 

2) Значение суммарной стоимости перевозок при переходе от одной к другой матрице связаны следующим соотношением: f^k+1=f^k + θ* Δ_ij

Где k это номер итерации.

θ и Δ_ij находятся на шагах 3 и 6.

 

 

2. Пример решения транспортной задачи методом потенциалов

1. Начальный план перевозок:

Общее число запасов на складах:

; Общая потребность:

	B1	B2	B3	B4	B5	Запасы
А1	*				*
А2		*	*		*
А3	*	*	*
потребители

Задача является закрытой.

N=7, n+m-1=5+3-1=7.

Общие затраты на перевозку всей продукции: F = 21740

2. Составляем уравнения вида di+Bj=Cij:

d1+B2=14

d1+B3=16

d1+B4=28

d2+B1=19

d2+B4=36

d3+B4=39

d3+B5=41.

Пусть d1=0, тогда d2=8, d3=11; B1=11, B2=14, B3=16, B4=28, B5=30

3. Вычисляем относительные оценки:

11=11

15=0

22=-5

23=2

25=-2

31=15

32=5

33=4

 

4. Строим означенный цикл

5.

	B1	B2	B3	B4	B5	Запасы
А1	*	14 -		28 +	*
А2		17 + *	*	36 -	*
А3	*	*	*
потребители		]140

	B1	B2	B3	B4	B5	Запасы
А1
А2
А3
потребители		]140

 

	B1	B2	B3	B4	B5
А1
А2
А3

В приведенной выше таблице нет отрицательных оценок (план улучшить нельзя), следовательно достигнуто оптимальное решение.

 

	B1	B2	B3	B4	B5
А1
А2
А3

Общие затраты на перевозку всей продукции, для оптимального плана составляют:

F=

 

 

 

Двойственная задача

1. Теоретические сведения

Каждую задачу ЛП можно определить обратно поставленной в соответствие другой задаче, тоже ЛП, которую называют двойственной по отношению к исходной задаче. Исходная и двойственная задача тесно связаны между собой и образуют единственную пару двойственных задач.

Часто бывает так, что задача в исходной формулировке сложна для решения. В этом случае проще перейти к двойственной задаче, решить ее и затем пересчитать и исследовать решение исходной задачи.

В зависимости от структуры модели исходной задачи различают симметричную, несимметричную и смешанную двойственные задачи.

Виды математических моделей двойственных задач:

1. Симметричная двойственная задача

Рассмотрим неканоническую модель исходной задачи ЛП. Ищем максимум целевой функции

L(x) = c₁*x₁ + … + c_n*x_n → max

при следующих ограничениях

a₁₁*x₁ + … + a_1n*x_n ≤ b₁ | y₁

a₂₁*x₁ + … + a_2n*x_n ≤ b₂| y₂

…………………………………………

a_m1*x₁ + … + a_mn*x_n ≤ b_m| y_m

x_j ≥ 0 (j = 1, n)

Составим математическую модель следующим образом:

1) Каждое неравенство системы ограничений исходной задачи привести в соответствие переменным y_i.

2) Составить целевую функцию, коэффициентами которой являются свободные члены системы ограничений исходной задачи.

3) Составить систему ограничений. Коэффициенты этой системы образуют транспонированием матрицы коэффициентов системы ограничений исходной задачи. При этом знаки неравенств меняются на противоположные. Свободные члены системы ограничений теперь являются коэффициентами целевой функции исходной задачи. Требование максимизации целевой функции заменить минимизацией и наоборот. Все переменные двойственной задачи неотрицательны.

Математическая модель двойственной задачи имеет следующий вид:

 

S(y) = b₁*y₁ + … + b_m*y_m→ min

a₁₁*x₁ + … + a_1m*y_m≥c₁

a₂₁*x₁ + … + a_2m*y_m≥c₂

…………………………………………

a_n1*x₁ + … + a_nm*x_m≥c_n

y_i ≥ 0 (i = 1, m)

 

2. Несимметричные двойственные задачи

 

Рассмотрим математическую модель исходной задачи в канонической форме

L(x) = c₁*x₁ + … + c_n*x_n → max

a₁₁*x₁ + … + a_1n*x_n ≤ b₁ | y₁

a₂₁*x₁ + … + a_2n*x_n ≤ b₂ | y₂

…………………………………………

a_m1*x₁ + … + a_mn*x_n ≤ b_m| y_m

x_j ≥ 0 (j = 1, n)

Составим математическую модель двойственной задачи. Для ее составления пользуемся тем же правилом, что и для составления симметричной задачи, но с учетом следующих особенностей. Ограничениями двойственной задачи будут неравенства. Если в целевой функции двойственной задачи требуется найти минимум, то знаки “≥”, если максимум, то “≤”. Переменные y_iпроизвольные по знаку, то есть могут принимать как положительные, так и отрицательные значения.

S(y) = b₁*y₁ + … + b_m*y_m → min

a₁₁*x₁ + … + a_1m*y_m ≥ c₁

a₂₁*x₁ + … + a_2m*y_m ≥ c₂

…………………………………………

a_n1*x₁ + … + a_nm*x_m ≥ c_n

Совместное рассмотрение пары двойственных задач имеет практическое значение, так как имея оптимальное решение одной задачи на основе теоремы двойственности можно найти оптимальное решение другой задачи, не решая ее.

3. Смешанные двойственные задачи

 

Математическая модель исходной задачи имеет условно симметричную и несимметричную задачи. При составлении двойственных задач необходимо выполнять правила составления симметричных и несимметричных задач.

Приведем основные теоремы, необходимые для решения двойственных задач:

1) Если одна из двойственных задач имеет оптимальное решение, то другая также имеет оптимальное решение, причем для любых оптимальных решений xиy выполняется равенство

L(x)_max = S(y)_min

Если одна из двойственных задач не имеет решения, то другая задача также не имеет допустимого решения.

2) Если в оптимальном решении одной из двойственных задач какая-либо переменная строго больше нуля, то соответствующее ей ограничение в другой двойственной задаче выполняется как строгое равенство, и наоборот, если при оптимальном решении одной из двойственных задач какое-либо ограничение выполняется как строгое неравенство, то соответствующая ему переменная в другой задаче равна нулю.

 

Пример решения двойственной задачи

1. -1x₁ + 1x₂ + 1x₃ = 1

1x₁ + 1x₂ + 1x₄ = 7

1x₁ + 1x₂ - 1x₅ = 3

Введем искусственные переменные x: в 3-м равенстве вводим переменную x₆;

-1x₁ + 1x₂ + 1x₃ + 0x₄ + 0x₅ + 0x₆ = 1

1x₁ + 1x₂ + 0x₃ + 1x₄ + 0x₅ + 0x₆ = 7

1x₁ + 1x₂ + 0x₃ + 0x₄-1x₅ + 1x₆ = 3

Для постановки задачи на минимум целевую функцию запишем так:

F(X) = 2x₁-3x₂+Mx₆ → min

Из уравнений выражаем искусственные переменные:

x₆ = 3-x₁-x₂+x₅

которые подставим в целевую функцию:

F(X) = (2-M)x₁+(-3-M)x₂+(M)x₅+(3M) → min

Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид:

 

Решим систему уравнений относительно базисных переменных:

x₃, x₄, x₆,

Полагая, что свободные переменные равны 0, получим первый опорный план:X1 = (0,0,1,7,0,3)

Базис	B	x1	x2	x3	x4	x5	x6
x3		-1
x4
x6						-1
F(X0)	3M	-2+M	3+M			-M

 

Базис	B	x1	x2	x3	x4	x5	x6	min
x3		-1
x4
x6						-1
F(X1)	3M	-2+M	3+M			-M

 

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x2		-1
x4				-1
x6				-1		-1
F(X1)	-3+2M	1+2M		-3-M		-M

 

Разрешающий элемент равен (2) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	min
x2		-1						-
x4				-1
x6				-1		-1
F(X2)	-3+2M	1+2M		-3-M		-M

 

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x2				1/2		-1/2	1/2
x4							-1
x1				-1/2		-1/2	1/2
F(X2)	-4			-21/2		1/2	-1/2-M

Разрешающий элемент равен (1) и находится на пересечении ведущего столбца и ведущей строки.

Базис	B	x1	x2	x3	x4	x5	x6	min
x2				1/2		-1/2	1/2	-
x4							-1
x1				-1/2		-1/2	1/2	-
F(X3)	-4			-21/2		1/2	-1/2-M

 

Получаем новую симплекс-таблицу:

Базис	B	x1	x2	x3	x4	x5	x6
x2				1/2	1/2
x5							-1
x1				-1/2	1/2
F(X3)	-6			-21/2	-1/2		-M

 

Конец итераций: индексная строка не содержит положительных элементов - найден оптимальный план

Окончательный вариант симплекс-таблицы:

Базис	B	x1	x2	x3	x4	x5	x6
x2				1/2	1/2
x5							-1
x1				-1/2	1/2
F(X4)	-6			-21/2	-1/2		-M

 

Оптимальный план можно записать так:

x₂ = 4

x₅ = 4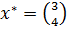

x₁ = 3

F(X) = -6

Составим двойственную задачу к прямой задаче.

- y₁ + y₂ + y₃≤2

y₁ + y₂ + y₃≤-3

y₁ + 7y₂ + 3y₃ → max

y₁ ≤ 0

y₂ ≤ 0

y₃ ≥ 0

Решение двойственной задачи дает оптимальную систему оценок ресурсов.

Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи.

Из теоремы двойственности следует, что Y = C*A^-1.

Составим матрицу A из компонентов векторов, входящих в оптимальный базис.

 

Определив обратную матрицу D = А^-1 через алгебраические дополнения, получим:

 

Как видно из последнего плана симплексной таблицы, обратная матрица A^-1 расположена в столбцах дополнительных переменных.

Тогда Y = C*A^-1 =

 

Оптимальный план двойственной задачи равен:

y₁ = -2¹/₂

y₂ = ^-1/₂

y₃ = 0
=

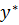Z(Y) = 1*-2¹/₂+7*^-1/₂+3*0 = -6