1. Теоретические сведения
Рассмотрим частный случай общей задачи нелинейного программирования 1,2, предполагая, что система ограничений 2 содержит только уравнения, отсутствует условие неотрицательности переменных и как целевая, так и функция ограничения непрерывны со своими частными производными.
f(x1, x2,..,xn) –> max(min) (3)
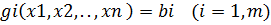(4)
В курсе математического анализа задачу 3,4 называют задачей на условный экстремум или классической задачей оптимизации.
Чтобы найти решение этой задачи вводят набор переменных 
которые называются множителями Лагранжа.
Далее составляют функцию Лагранжа:
F(x1, x2,..,xn ,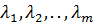 
) = F(x1, x2,.., 
)+ 
(5)
Далее находим частные производные
= 
- 
=0, j=(1,n) (6)
= 
- 
i=(1,m)
Всякое решение системы (6) определяет точку x, в которой может иметь место экстремум функции f. Следовательно, решив систему (6) получают все точки, в которых функция 3 может иметь экстремальное значение.
Дальнейшее исследование найденных точек проводят так же, как и в случаях безусловного экстремума.
Т.о. определение экстремальных точек задачи 3,4 методом Лагранжа включает следующие этапы:
1. Составляют функцию Лагранжа
2. Находят частные производные от функции Лагранжа по переменным 
и приравнивают их к 0.
3. Решая систему 6, находят точки, в которых целевая функция может иметь экстремум.
4. Среди точек, подозрительных на экстремум, находят такие, в которых достигается экстремум, и вычитают значение функции 3 в этих точках.
2. Пример решения задачи методом множителей Лагранжа
x1 + x2 + x3 = 18
z= 
→ max
F(x)=f(x)+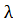 
(18- x1 - x2 - x3)
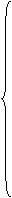F(x1,x2,x3, )= 
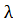(18- x1 - x2 - x3)
=0
=0
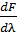=0
=0
F(x1)=2x1 
- 
F(x2)= 
-
F(x3)= 
18- x1 - x2 - x3 =0
x1=4; x2=6; x3=8
= 
z=14155776
Метод штрафных функций
1. Теоретические сведения
Рассмотрим задачу определения максимального значения вогнутой функции f(x1, x2,..,xn) при следующих условиях:
где 
Вместо того, чтобы непосредственно решать эту задачу, находят максимальное значение функции F(x1, x2,..,xn)=f(x1, x2,..,xn)+H(x1, x2,..,xn).
Здесь H – функция, определяемая системой ограничений (штрафная функция).
Штрафную функцию можно построить различными способами. Однако, наиболее часто она имеет вид:
H(x1, x2,..,xn) = 
= 
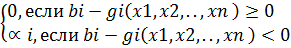(1)
где 
>0 – некоторые постоянные числа, представляющие собой весовые коэффициенты.
Используя штрафную функцию переходят от одной точки к другой до тех пор, пока не получат приемлемое решение.
При этом, координаты последующей точки находят по следующей формуле:
(2)
где 
Из соотношения (2) следует, что если предыдущая точка находится в ОДР исходной задачи, то второе слагаемое в квадратных скобках равно нулю и переход к последующей точке определяется только градиентом целевой функции.
Если же указанная точка не принадлежит ОДР, то за счет данного слагаемого на последующих итерациях достигается возвращение в ОДР.
При этом, чем < , тем быстрее находится приемлемое решение. Однако, точность его определения снижается.
Поэтому итерационный процесс обычно начинают при сравнительно малых значениях и, продолжая его, эти значения постепенно увеличивают.
Этапы решения:
1. Определяют исходное допустимое решение (x0);
2. Выбирают шаг вычислений (
);
3. Находят по всем переменным частные производные от целевой функции и функций, определяющих ОДР задачи;
4. По формуле (2) находят координаты точки, определяющие возможное новое решение задачи;
5. Проверяют, удовлетворяют ли координаты найденной точки системе ограничений задачи. Если нет, то переходят к следующему этапу. Если координаты точки определяют допустимое решение задачи, то исследуют необходимость перехода к последующему допустимому решению. В случае такой необходимости, переходят к этапу 2. В противном случае, найдено приемлемое решение исходной задачи.
6. Устанавливают значения весовых коэффициентов 
и переходят к этапу 4.
2. Пример решения задачи методом штрафных функций