ОСНОВНЫЕ ТЕОРЕМЫ О ПРЕДЕЛАХ.

ОСНОВНЫЕ СВОЙСТВА ФУНКЦИИ»

МОНОТОННОСТЬ ФУНКЦИИ.

Функция у= f (х) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции, т.е. если , то .

Функция у=f(х) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции, т.е. если , то .

Функцию, которая на заданном промежутке только возрастает или только убывает, называют монотонной на этом промежутке. О монотонности функции можно судить по ее графику.

 

x

b

a

y

y=f1(x)

y=f3(x)

y=f2(x)

y=f₁(x) возрастает на [a; b] – монотонная;

y=f₂(x) убывает на [a; b] – монотонная;

y=f₃(x) возрастает на [a; x₀) и убывает на (x₀; b] – не является монотонной.

 

ЧЕТНОСТЬ – НЕЧЕТНОСТЬ ФУНКЦИИ

Функция y=f(x) называется четной на D(у),если для любого xÎD(у) и -хÎD(у) и имеет место равенство: f(-x) = f(x).

График четной функции симметричен относительно оси Оу.

Функция y=f(x) называется нечетной на D(у), если для любого хÎD(у) и -хÎD(у) и имеет место равенство: f(-x) = - f(x).

График нечетной функции симметричен относительно начала координат.

 

Не всякая функция является четной или нечетной, обычно такую функцию называют функцией общего вида.

 

ПЕРИОДИЧНОСТЬ ФУНКЦИИ

Функция y=f(x)называется периодической с периодом Т, если для любого хÎD(f) числа х+Т и х-Т также принадлежат D(f) и имеет место равенство:f(x+T)=f(x-T)=f(x).

Если Т – период функции, то k× T, где kÎ Z, k≠О, также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период. Значения периодической функции через промежуток, равный периоду, повторяются. Этим пользуются при построении графиков периодических функций.

При вычислении периодов тригонометрических функций целесообразно использовать следующие соотношения:

1.

2.

3.

 

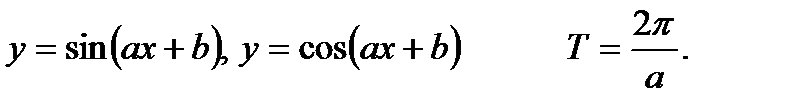
ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И НУЛИ ФУНКЦИИ.

Значения аргумента х из области определения функции у = f (х), при которых соответствующие значения функции равны нулю, называются нулями функции.

Значения аргумента, при которых функция обращается в нуль, - это абсциссы точек пересечения графика функции с осью Ох.

 

Числовые промежутки, на которых функция сохраняет свой знак, т.е. остается положительной или отрицательной, называются промежутками знакопостоянства функции.

Промежутки знакопостоянства – это промежутки между нулями функции, т.к. при переходе через нуль функция меняет свой знак на противоположный. О промежутках знакопостоянства и нулях функции легко судить по ее графику.

 

x3

x4

x2

x1

x0

x

y

>0

<0

x₀, x₁, x₂, x₃, x₄ – нули функции;

f(x) >0 на (x₀; x₁); (x₂; x₃); (x₄; +¥0 - промежутки знакопостоянства,

f(x) <0 на (-¥; x₀); (x₁; x₂); (x₃; x₄) - промежутки знакопостоянства.

«ПРЕДЕЛ ФУНКЦИИ»

 

ОСНОВНЫЕ ТЕОРЕМЫО ПРЕДЕЛАХ.

 

- справедливы как для пределов числовых последовательностей, так и для пределов функций при и при .

1.Теорема о единственности предела.

- единственный.

2.Предел суммы равен сумме пределов

3.Предел произведения равен произведению пределов

4.Предел частного равен частному пределов, если предел делителя отличен от нуля:

5.Постоянный множитель выносится за знак предела

6.Предел постоянной равен самой постоянной:

7.Предел сложной функции:

если и ,

то , где f(u(x)) –сложная функция.

8.Предел степени равен степени предела:

.

 

ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ.

а) ДЛЯ ФУНКЦИЙ

		,

 

«НЕПРЕРЫВНОСТЬ ФУНКЦИИ»

Определение: функция у=f(x) в точке х₀ является непрерывной тогда и только тогда, когда выполняются условия:

1. функция у=f(x) определена в точке х₀ , т.е. существует f(x₀);

2. для функции у=f(x) существует конечный предел ;

3. 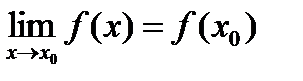,т.е. значение функции в этой точке и значение предела совпадают.

Примеры:

у 2

0 1 х 0 1 х

у 2

у=f1(x)

y=f2(x)

0 1 х 0 1 х

y=f3(x)

y=f4(x)

y 2 1

y 2 1

Исследуем каждую из приведенных функций на непрерывность в точке х=1 согласно приведенному определению:

1).

2).

3).

4).

 

Определение: еслифункция у=f(x) непрерывна в каждой точке некоторого промежутка, то ее называют непрерывной на данном промежутке.

 

ТЕОРЕМА 1: Если у=f(x) и у=g(x) непрерывны в точке х₀,то в точке х₀ будут непрерывны функции и .

ТЕОРЕМА 2: Если у=f(x) и у=g(x) непрерывны в точке х₀ и , то в точке х₀ будут непрерывны функции .

 

Следствие из теорем 1,2: Непрерывными во всех точках области определения являются функции:

ü многочлен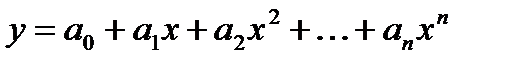

ü дробно-рациональная функция

ü тригонометрические функции , , ,

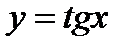ü обратные тригонометрические функции , , ,

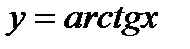ü функции , , ,

 

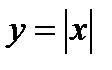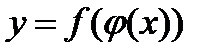ТЕОРЕМА 3: Если функция у=f(u) непрерывна в точке u₀, а функция непрерывна в точке , то сложная функция непрерывна в точке x₀.

 

«ПРОИЗВОДНАЯ ФУНКЦИИ»

Производной функции y=f(x) в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:

 

«ТАБЛИЦА ПРОИЗВОДНЫХ»

 

1. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ:

 

 

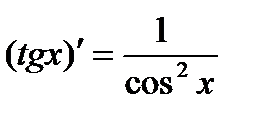
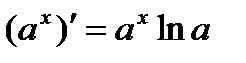
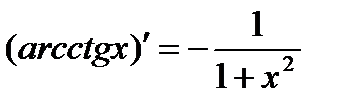
2. ТЕОРЕМЫО ПРОИЗВОДНЫХ:

1. Производная суммы-разности двух функций:

2. Производная произведения двух функций:

3. Вынесение числового множителя за знак производной:

, где с -число.

4. Производная частного двух функций:

.

 

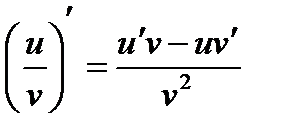3. СЛОЖНАЯ ФУНКЦИЯ y = f (g (x)), где y=f (u), u=g (x):

4. ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ :

.

 

5. ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ НЕЯВНО F (x; y)=0:

 

Для нахождения производной по х функции у дифференцируем обе части равенства F (x; y(х))=0, учитывая, что у зависит от х, т.е., рассматриваем ее как сложную функцию, а затем получившееся равенство разрешаем относительно .

 

6. ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ:

, где t – параметр, находится по формуле .

7. ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ:

 

Так как производная функции с одной переменной также является функцией с одной переменной, то от нее также можно находить производную, которую называют производной второго порядка:

 

Аналогично определяют производные более высоких порядков.