Есть биномиально распределенная случайная величина (берется из схемы Бернулли (схема независимых испытаний, успех – p, неудача – q)). Тогда вероятность того, что в событие A при n испытаниях появится точно m раз, стремится к нормальному распределению:
где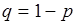 
; 
.
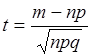22. Интегральная предельная теорема Муавра-Лапласа
Интегральная предельная теорема:
Если вероятность «p» события «A» в каждом испытании постоянна и отлична от 0 и 1, то вероятность «P(a, b)» того, что событие «A» появится в «n» испытаниях от «a» до «b» раз, приближенно равна определенному интегралу:
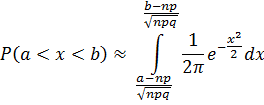
23. Математическое ожидание случайной величины и его свойства
математическое ожидание – среднее значение случайной величины.
Свойства мат. ожиданий:
1) E * const = const
2) E (cX) = c E(X)
3) E(X+Y) = EX + EY
4) E(XY) = E(X) * E(Y) (только для независимых случайных величин)
отняв мат ожидание от случайной величины - центрирование
24. Статистическое оценивание математического ожидания случайной величины
Пусть x1, x2, x3,…, xn – это n независимых наблюдений
величины Х, тогда для оценки математического ожидания случайной величины используют статистику X:
Эта оценка является состоятельной, несмещенной и эффективной.
25. Дисперсия случайной величины и ее свойства
дисперсия – разброс значений, которые может принимать случайная величина.
Свойства дисперсии:
1) D * const =0
2) D (cX) = c2 DX
3) D(X+Y) = DX + DY (только для независимых случайных величин)
стандартное отклонение – корень из дисперсии
деление на стандартное отклонение - нормирование
26. Статистическое оценивание дисперсии случайной величины
Как нам оценить дисперсию?
Да вот так:
– эта хрень называется «несмещенная оценка дисперсии»
Как бы ES2 = DX. Пам. пам. пам.
27. Оценка вероятности по частоте
При проведении экспериментов часто приходится оценивать неизвестную вероятность события P по его частоте X со шрихом (нет символа ^_^) в N независимых экспериментах. Частота некоторого события в N независимых экспериментах есть не что иное, как среднее арифметическое наблюдаемых значений величины Х, которая в каждом отдельном опыте принимает значение 1 (если событие совершилось), или значение 0 (если событие не произошло):
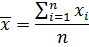
28. Закон больших чисел
закон больших чисел – чем больше раз повторять случайный эксперимент, тем с меньшей вероятностью случайная величина отклонится от своего мат. ожидания (на нем основан статистический метод)
29. Доверительное оценивание параметров распределений
Какова точность оценки параметра? В каких границах он может лежать?
Доверительная область – это область в пространстве параметров, в которую с заданной вероятностью входит неизвестное значение оцениваемого параметра распределения. «Заданная вероятность» называется доверительной вероятностью и обычно обозначается γ (гамма)
30. Построение доверительного интервала для матожидания нормального распределения
Центрирование случайной величины – когда от нее отнимают ее мат ожидание, и получают новую случ. величину, у которой мат. ожидание = 0.
P(a < EX < b) = γ
a, b – доверительный интервал
Если задана доверительная вероятность, то a и b выглядят так:
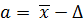
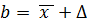
Где 
– величина доверительного интервала
31. Построение доверительного интервала для дисперсии нормального распределения
Процедура деления случайной величины на ее стандартное отклонение приводит к тому, что ее DX = 1 – нормирование случайной величины
Не знаю, к чему я это вчера написал, но суть в том, что:
(D-t < D < D+t) – доверительный интервал
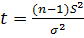– формула доверительного интервала для дисперсии. S2 – несмещённая оценка дисперсии; σ – среднее квадратичное отклонение
32. Статистические гипотезы. Проверка статистических гипотез
Проверки статистических гипотез — один из классов задач в математической статистике.
Пусть в (статистическом) эксперименте доступна наблюдению случайная величина X, распределение которой P известно полностью или частично. Тогда любое утверждение, касающееся P, называется статистической гипотезой.
На практике обычно требуется проверить какую-то конкретную гипотезу H0. Такую гипотезу принято называть нулевой. При этом параллельно рассматривается противоречащая ей гипотеза H1, называемая конкурирующей или альтернативной.
В большинстве случаев статистические критерии основаны на случайной выборке (X1, X2, …, Xn) фиксированного объема n >= 1 из распределения P. В последовательном анализе выборка формируется в ходе самого эксперимента и потому её объем является случайной величиной.
Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости.
33. Вероятности ошибок первого и второго рода
Проверка статистической гипотезы означает проверку согласования исходных выборочных данных с выдвинутой основной гипотезой. При этом возможно возникновение двух ситуаций – основная гипотеза может подтвердиться, а может и опровергнуться. Следовательно, при проверке статистических гипотез существует вероятность допустить ошибку, приняв или опровергнув верную гипотезу.
При проверке статистических гипотез можно допустить ошибки первого или второго рода
Ошибкой первого рода (ошибка альфа) называется ошибка, состоящая в опровержении верной гипотезы.
Ошибкой второго рода (ошибка бета) называется ошибка, состоящая в принятии ложной гипотезы.
Уровнем значимости a называется вероятность совершения ошибки первого рода.
Значение уровня значимости а обычно задаётся близким к нулю, потому что чем меньше значение уровня значимости, тем меньше вероятность совершения ошибки первого рода, состоящую в опровержении верной гипотезы Н0.
| Верная гипотеза | |||
| H0 | H1 | ||
| Результат применения критерия | H0 | H0 верно принята | H1 неверно принята (Ошибка второго рода) |
| H1 | H0 неверно отвергнута (Ошибка первого рода) | H0 верно отвергнута |
34. Построение статистических критериев.
Статистический критерий — строгое математическое правило, по которому принимается или отвергается та или иная статистическая гипотеза с известным уровнем значимости.
Построение критерия представляет собой выбор подходящей функции от результатов наблюдений (ряда эмпирически полученных значений признака), которая служит для выявления меры расхождения между эмпирическими значениями и гипотетическими.
35. Статистические критерии согласия.
Критерии согласия. Проверка на согласие подразумевает проверку предположения о том, что исследуемая случайная величина подчиняется предполагаемому закону. (Например, закон, что вероятность того, что на игральной костяшке выпадет 1,2,3,4,5 или 6 равна 1/6).
+ предыдущий вопрос