Функциональные уравнения

Пример 1.

1) Пусть

2) Подставим в исходное уравнение, получим

3)Заменим z на получим или после преобразований в правой части уравнения:

4)Итак, получили два уравнения:

5)Умножим обе части 1-го уравнения на (-2) и сложим со 2-ым уравнением, получим:

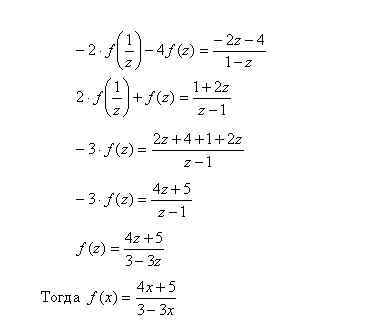
Пример 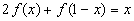2. ²

1)Заменим в уравнении на ,получим ² .

2) Умножим обе части исходного уравнения 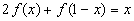² на (-2) и сложим с уравнением ²,

получим:

.

Пример 3.

1. Пусть тогда уравнение принимает вид: .
2. Заменим в уравнении на , получим .
3. Умножим уравнение 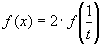на (-2) и сложим с уравнением , получим Таким образом,

Пример 4.

1) Заменим в уравнение на , .

2)Умножим уравнение на и вычтем из уравнения ,получим -

, где

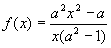
Пример 5.

,

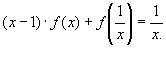1)Заменим в уравнении на получим .

2)Выразим из исходного уравнения , получим

или .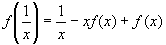

3)Подставим в уравнение ,получим .

Выполним преобразования

Пример 6.

.

1. Заменим на , получим
2. Умножим обе части уравнения на и вычтем из уравнения

получим

Пример 7.

1)Пусть , тогда уравнение принимает вид:

2)Пусть тогда исходное уравнение принимает вид:

3)Умножим обе части уравнения из п.1 на 2, а обе части уравнения из п.2 на (-3) и почленно сложим получившиеся уравнения:

Пример 8.

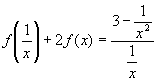1) Заменим на , получим или .

2)Умножим обе части уравнения из п.1 на (-2) и сложим с исходным уравнением:

получаем:

Литература

1. Кострикина Н.П. “Задачи повышенной трудности в курсе алгебры 7-9 классов” - М: “Просвещение”, 1991г.
2. Смышляев В.К.. Практикум по решению задач школьной математики. – М: “Просвещение”, 1978г.

 

 

Введение
Функциональное уравнение это уравнение, в котором неизвестными
являются функции (одна или несколько). Например,
f(x)+xf(x+1) = 1
Некоторые фу нкциональны е уравнения знакомы нам еще из школьного
курса это f(x) = f(-x), f(-x) = f(x), f(x+T) = f(x), которые задают
такие свойства функций, как чётность, нечётность, периодичность.
Задача решения функциональных уравнений является одной из самых
старых в математическом анализе. Они появились почти одновременно с
зачатками теории функций. Первый настоящий расцвет этой дисциплины
связан с проблемой параллелограмма сил. Ещё в 1769 году Даламбер свёл
обоснование закона сложения сил к решению функционального уравнения
(1)
То же уравнение и с той же целью было рассмотрено Пуассоном в 1804
году при некотором предположении аналитичности, между тем как в 1821
году Коши (1789 – 1857) нашёл общие решения
этого уравнения, предполагая только непрерывность f (x).
Даже известная формула неевклидовой геометрии для угла параллельности

была получена Н. И. Лобачевским (1792 – 1856) из функционального
уравнения
, (2)
которое он решил методом, аналогичным методу Коши. Э то уравн ение
можно привести к уравнению
.
Ряд геометрических задач, приводящих к функциональным уравнениям,
рассматривал английский математик Ч. Баббедж (1792— 1871). Он
изучал, например, периодические кривые второго порядка, определяемые
следующим свойством для любой пары точек кривой: если абсцисса второй
точки равна ординате первой, то ордината второй точки равна абсциссе
первой. Пусть такая кривая является графиком функции у = f (х); (х, f
(х)) — произвольная ее точка. Тогда, согласно условию, точка с
абсциссой f (х) имеет ординату х. Следовательно,
(3)
Функциональному уравнению (3) удовлетворяют, в частности, функции:
,
Одними из простейших функциональных уравнений являются уравнения Коши

f(x+y) = f(x)+f(y), (4)
f(x+y) = f(x) · f(y), (5)
f(xy) = f(x)+f(y), (6)
f(xy) = f(x) · f(y),

 

 

Эти уравнения Коши подробно изучил в своём (Курсе Анализа), изданном
в 1821 году. Непрерывные решения этих четырёх основных уравнений имеют
соответственно вид
,,,
В классе разрывных функций могут быть и другие решения. Уравнение (4
) ранее рассматривалось Лежандром и Гауссом при выводе основной
теоремы проективной геометрии и при исследовании гауссовского закона
распределения вероятностей.
Функциональное уравнение (4) было опять применено Г. Дарбу к
проблеме параллелограмма сил и к основной теореме проективной
геометрии; его главное достижение значительное ослабление
предположений. Мы знаем, что функциональное уравнение Коши (4)
характеризует в классе непрерывных функций линейную однородную функцию
f (x) = ax. Дарбу же показал, что всякое решение, непрерывное хотя
бы в одной точке или же ограниченное сверху (или снизу) в произвольно
малом интервале, также должно иметь вид f (x) = ax. Дальнейшие
результаты по ослаблению предположений следовали быстро один за другим
(интегрируемость, измеримость на множестве положительной меры и даже
мажорируемость измеримой функцией). Возникает вопрос: существует ли
хоть одна какаянибудь аддитивная функция (т. е. удовлетворяющая (4
)), отличная от линейной однородной. Найти такую функцию действительно
нелегко! В ходе работы мы покажем, что при рациональных x значения
любой аддитивной функции должны совпадать со значениями некоторой
линейной однородной функции, т. е. f (x) = ax для x Q. Казалось бы,
что тогда f (x) = ax для всех действительных x. Если f (x)
непрерывна, то это действительно так, если же данное предположение
отбросить то нет. Первый пример отличного от f (x) = ax разрывного
решения функционального уравнения (4) построил в 1905 году немецкий
математик Г. Гамель с помощью введённого им базиса действительных
чисел.
Многие функциональные уравнения не определяют конкретную функцию, а
задают широкий класс функций, т. е. выражают свойство, характеризующее
тот или иной класс функций. Например, функциональное уравнение f (x
+1) = f (x) характеризует класс функций, имеющих период 1, а
уравнение f (1+ x) = f (1x) класс функций, симметричных относительно
прямой x = 1, и т. д.
Вообще, для функциональных уравнений, не сводящихся к
дифференциальным или интегральным, известно мало общих методов
решения. Далее будут рассмотрены некоторые приёмы, позволяющие решать
функциональные уравнения.

 

Функциональные уравнения

Функциональное уравнение — это уравнение, в котором неизвестными являются функции (одна или несколько). Например,

Решить функциональное уравнение — значит, найти неизвестную функцию, при подстановке которой в исходное функциональное уравнение оно обращается в тождество (если неизвестных функций несколько, то необходимо найти их все).

Соотношения, задающие функциональные уравнения, являются тождествами относительно некоторых переменных, а уравнениями их называют потому, что неизвестные функции — искомые.

Многие функциональные уравнения содержат несколько переменных. Все эти переменные, если на них не наложены какие-то ограничения, являются независимыми.

Всегда четко должно быть оговорено, на каком множестве функциональное уравнение задается, т.е. какова область определения каждой неизвестной функции. Общее решение функционального уравнения может зависеть от этого множества.

Кроме области определения функций, важно знать, в каком классе функций ищется решение. Количество и поведение решений очень строго зависит от этого класса.

Вообще для функциональных уравнений, не сводящихся к дифференциальным или интегральным, известно очень мало общих методов решения. Рассмотрим основные приемы, помогающие найти решения таких уравнений.

Идея непрерывности

Определение. Функция называется непрерывной в точке , если выполняются следующие два условия:

1) точка принадлежит области определения функции ;

2) , разумеется, в предположении, что этот предел существует.

Если хотя бы одно из этих условий нарушается, функция не является непрерывной в точке , она будет разрывной в этой точке.

Определение. Функция называется непрерывной на отрезке , если она непрерывна во всех точках этого отрезка.

Справедлива следующая теорема:

Теорема Больцано — Коши. Если функция непрерывна на отрезке и на концах этого отрезка принимает неравные значения и , то она принимает все промежуточные между и значения на отрезке .

Пример 1. Функция непрерывна на всей вещественной прямой и удовлетворяет равенству для всех . Доказать, что уравнение имеет хотя бы одно решение.

Решение. Рассмотрим функцию . Предположим, что для всех . Тогда в силу непрерывности либо для всех , либо для всех . (Если бы существовали такие и , что , то по теореме Больцано — Коши, внутри отрезка была бы точка, в которой обращалась бы в нуль, что противоречит предположению.

Пусть для определенности , то есть для всех . Обозначим . Тогда, так как , то , что противоречит тому, что . Значит, при некотором имеем .

Пример 2. Функция задана на всей вещественной оси, причем выполняется равенство

Доказать, что не может быть непрерывной.

Решение. Функция не может принимать значение . Действительно, при имеем . Значит, для всех или . Выразим из нашего равенства :

Значит, неравенство невозможно, иначе .

Если же , то должно выполняться неравенство , откуда и

следовательно, получаем, что . Противоречие.

Пример 3. Найти все непрерывные функции , удовлетворяющие соотношению для любого .

Решение. В данное уравнение подставим вместо (это можно сделать, так как функция определена для всех ), и еще несколько раз проделаем то же самое, получим

По непрерывности функции в нуле имеем

Получили, что , то есть функция — постоянная.

Уравнения Коши

1. Уравнение

в классе непрерывных функций имеет решение .

Такое же решение оно имеет и в классе монотонных функций.

2. Уравнение

в классе непрерывных функций имеет решение (если не считать .

3. Уравнение

в классе непрерывных функций имеет решение (если не считать ).

4. Уравнение

в классе непрерывных функций имеет решение (если не считать ).