Основные элементарные функции комплексного переменного находятся по формулам:
Гиперболические функции связаны с тригонометрическими функциями следующими соотношениями:
; 
; 
; 
.
Функция 
для каждого 
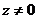определена однозначно и называется главным значением логарифма числа 
. Функция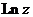 
в отличие от для каждого 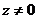принимает бесконечно много значений, т. е. представляет собой бесконечное множество комплексных чисел:
Тем же свойством обладает и степенная функция 
, если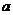 
– недействительное или действительное иррациональное число. Если 
– целое число, то функция однозначна и находится по формуле
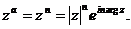
Если 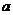– рациональное нецелое число, представимое в виде несократимой дроби 
то принимает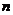 
различных значений:
Множество 
, 
есть множество решений уравнения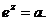 
Пусть в промежутке 
действительной оси задана непрерывная комплекснозначная функция
Тогда образ промежутка 
на расширенной комплексной плоскости 
при отображении 
называется непрерывной кривой.
Направление движения точки z, соответствующее возрастанию параметра 
, называется положительным направлением кривой.
Кривая, заданная параметрическим уравнением , 
называется гладкой, если производная
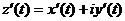
непрерывна и отлична от нуля в промежутке , причем 
если кривая замкнутая.
Множество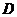 
точек расширенной комплексной плоскости называется областью, если оно
1) открытое, т.е. с каждой своей точкой содержит некоторую окрестность этой точки;
2) связное, т. е. любые две точки множества можно соединить непрерывной кривой, состоящей лишь из точек этого множества.
За положительное направление границы области берется то, при котором область остается слева.
Теоретические упражнения
1. Доказать, что для любого комплексного числа справедливы формулы:
1)  ;
| 5)  ;
|
2)  ;
| 6)  ;
|
3)  ;
| 7) 
|
4)  ;
| 8)  .
|
2. Доказать, что для любых комплексных чисел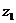 
и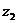 
справедливы формулы:
;
.
Задачи
1. Найти действительные и мнимые части следующих значений функций: а) 
; б) 
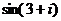; в) 
.
Решение:
а) по формуле экспоненты
.
Значит,
б) По формуле синуса суммы имеем
.
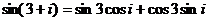Так как 
, а 
, то
.
Значит,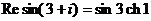 
, 
.
в) Так как 
(рис.10), то
2. Найти все значения:
а) Ln (-1 + i); б) 
Решение:
а) Используя результат пункта «в» предыдущей задачи, получим:
б) Согласно формуле для , 
Так как 
(рис.11), то
и
3. Решить уравнение: 
Решение. Подставив вместо 
и 
их выражения через 
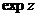, получим:
.
Обозначив 
, получим:
или
.
Решая это квадратное уравнение, находим:
, 
.
Для нахождения имеем следующие уравнения:
1. 
.
Так как 
- действительное положительное число, то главное значение его аргумента равно нулю и
, откуда
.
2. 
.
Так как 
- действительное отрицательное число, то главное значение его аргумента равно 
и
, откуда
.
Итак, исходное уравнение имеет бесконечное множество решений:
; 
.
4. Изобразить кривые, заданные следующими параметрическими уравнениями, и указать их направления:
а) 
;
б) 
;
в) 
;
г) 
Решение:
а) пусть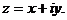 
Тогда из параметрического уравнения 
получим:
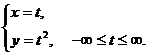
Это есть парабола, ориентированная слева направо (рис.12). Причем ее следует рассматривать как замкнутую на 
кривую.
б) Уравнение 
задает на плоскости упорядоченное множество точек , расстояние от которых до начала координат равно 
и таких, что угол между действительной осью и вектором 
равен и меняется от 0 до 
. Это будет
верхняя половина окружности радиуса R с центром в начале координат, ориентированная против часовой стрелки (рис.13).
в) Запишем уравнение в параметрическом виде:
.
Когда меняется от 
до 
, координата 
меняется от 
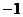до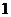 
, а когда меняется от до 
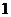, тогда уменьшается от до 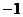. Следовательно, эта система уравнений определяет на плоскости отрезок с концами в точках 
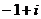и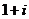 
, проходимый дважды: сначала от точки 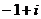к точке 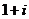, а затем от точки 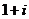к точке 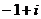(рис.14).
г) В данном случае:
или 
, 
.
Подставив данные выражения для 
в тождество 
, получим эллипс 
, обходимый по часовой стрелке (рис.15), т. к. если меняется от 0 до , то меняется от 
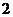до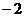 
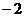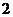и y < 0, а если меняется от до 2 , то меняется от до и 
.
5. Доказать, что кривая, заданная уравнением 
является гладкой.
Доказательство. Найдем производную по параметру
Очевидно, 
непрерывна при 
. Так как
всегда строго больше нуля, то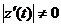 
, откуда следует: 
Выполнение всех этих условий и означает гладкость кривой.
6. Изобразить область и указать направление границы, если область содержит точку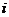 
и граница области задана условием:
Решение. Множество точек плоскости, удовлетворяющих условию 
, есть совокупность двух выходящих из начала координат и составляющих с действительной осью соответственно углы 
и 
. Эти лучи делят плоскость на две области, одна из которых содержит точку 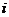. Направление границы – снизу вверх (рис.16).
