Методические указания и задания
К контрольным работам студентов
II курса заочного отделения
Для ЗРФ
Составители: Ваксман К.Г.
Михайлова А.В.
Москва,
2006 г.
Контрольная работа № 7 для ЗРФ
Тема: «Дифференциальное исчисление функций нескольких переменных и
Кратные интегралы»
Краткие теоретические сведения.
- Частные производные первого порядка. Дана функция
 .
.
При нахождении частной производной по одному аргументу второй аргумент считается постоянной величиной
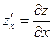 (аргумент у – постоянная величина);
(аргумент у – постоянная величина);  (аргумент х – постоянная величина)
(аргумент х – постоянная величина)
Например: 1)  ,
,  ;
;
2)  ,
, 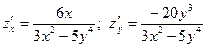 (используем формулу
(используем формулу  ).
).
Частные производные второго порядка находятся как производные от производных первого порядка.
 ;
;  ;
;  ;
; 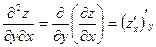 .
.
2.1. Полным дифференциалом функции  называется главная линейная часть приращения функции при приращении аргументов
называется главная линейная часть приращения функции при приращении аргументов  и
и  , отличающаяся от полного приращения функции на бесконечно малую величину высшего порядка относительно
, отличающаяся от полного приращения функции на бесконечно малую величину высшего порядка относительно  и
и  .
.
Пусть дана функция  и точка
и точка  . Полным дифференциалом
. Полным дифференциалом  при приращении
при приращении  и
и  будет
будет  .
.
2.2 Уравнение касательной плоскости к поверхности  в точке
в точке 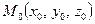
 .
.
3. Двойной интеграл
3.1 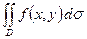 – это двойной интеграл от функции
– это двойной интеграл от функции  по области
по области  ,
, 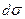 – это элемент площади области. Геометрический смысл двойного интеграла при
– это элемент площади области. Геометрический смысл двойного интеграла при 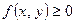 , при
, при 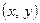 в области
в области  – это объём цилиндрического тела, ограниченного сверху поверхностью
– это объём цилиндрического тела, ограниченного сверху поверхностью  , с боков – цилиндрической поверхностью с образующими, параллельными оси z, снизу – плоской фигурой
, с боков – цилиндрической поверхностью с образующими, параллельными оси z, снизу – плоской фигурой  на плоскости
на плоскости  .
.
3.2 Если  , то двойной интеграл
, то двойной интеграл 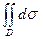 численно равен площади S области
численно равен площади S области  .
.
3.2.1 Двойной интеграл вычисляется сведением к вычислению двух повторных определённых интегралов.
3.2.2 Вычисление двойного интеграла в декартовой системе координат  .
.
а) необходимо построить область интегрирования  в плоскости
в плоскости  .
.
б) установить порядок интегрирования.







 в) Пусть область
в) Пусть область  заключена внутри прямоугольника:
заключена внутри прямоугольника: 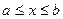 ,
,  , стороны которого касаются границы области в точках
, стороны которого касаются границы области в точках 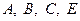 . Точками
. Точками  и
и  граница области разбивается на две линии ABC и AEC, каждая из которых пересекается с любой прямой, параллельной оси у в одной точке. Поэтому их уравнения можно записать так: линия ABC:
граница области разбивается на две линии ABC и AEC, каждая из которых пересекается с любой прямой, параллельной оси у в одной точке. Поэтому их уравнения можно записать так: линия ABC:  ; линия AEC:
; линия AEC: 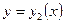 . Аналогично, точками В и Е граница разбивается на линии ВАЕ:
. Аналогично, точками В и Е граница разбивается на линии ВАЕ:  и ВСЕ:
и ВСЕ: 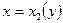 .
.
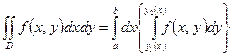 .
.
Сначала вычисляем «внутренний» (в  ) интеграл по у, считая х постоянной, а затем вычисляем «внешний» интеграл от полученной функции по х. Можно изменить порядок интегрирования:
) интеграл по у, считая х постоянной, а затем вычисляем «внешний» интеграл от полученной функции по х. Можно изменить порядок интегрирования:  .
.
г) Для вычисления площади 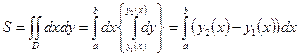 или при другом порядке интегрирования
или при другом порядке интегрирования 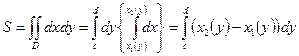 .
.


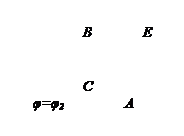 3.2.3 Вычисление площади в полярных координатах
3.2.3 Вычисление площади в полярных координатах 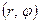 . Совместим начало декартовой системы координат с полюсом, а ось ох с полярной осью. Тогда
. Совместим начало декартовой системы координат с полюсом, а ось ох с полярной осью. Тогда  ,
,  ,
, 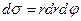 .
.




|
 заключена между линиями
заключена между линиями 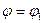 и
и  , которые касаются границы области в точках А и В, разделяющими границу на две линии.
, которые касаются границы области в точках А и В, разделяющими границу на две линии.  и
и  .
.
а) Пусть полюс не содержится внутри области интегрирования  .
.
б) Пусть полюс находится внутри или на границе области интегрирования  ,
,
 .
.
Примечание. При вычислении интегралов полезно воспользоваться формулами тригонометрии 
 , а также
, а также  ,
,  ,
, 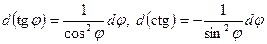 .
.
4. Тройной интеграл
4.1. 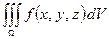 – это тройной интеграл от функции
– это тройной интеграл от функции  по пространственной области
по пространственной области  ,
,  – это элементы объема области
– это элементы объема области  .
.
Физический смысл тройного интеграла 4.1:
при  в области
в области  – это
– это
масса неоднородного тела в области 
с плотностью 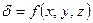 .
.
4.2. Если  в области
в области  , то тройной интеграл численно равен объему тела
, то тройной интеграл численно равен объему тела  .
.  .
.
4.3. Вычисление тройного интеграла в декартовой системе координат  .
.  .
.
4.3.1. Необходимо построить или хотя бы схематически представить пространственную область  .
.
4.3.2. Опишем около  цилиндрическую поверхность с образующей, параллельной оси
цилиндрическую поверхность с образующей, параллельной оси  . Она касается области
. Она касается области  вдоль линии
вдоль линии  , которая делит поверхность, ограничивающую область на 2 части: нижнюю
, которая делит поверхность, ограничивающую область на 2 части: нижнюю  и верхнюю
и верхнюю  .
.
4.3.3. Этой цилиндрической поверхностью тело  спроектируется на плоскость
спроектируется на плоскость  в область D, линия
в область D, линия  спроектируется на границу области D. Необходимо построить в плоскости
спроектируется на границу области D. Необходимо построить в плоскости  область D.
область D.
4.3.4. Вычисление тройного интеграла сведем к повторному интегрированию сначала по направлению оси z от  до
до  , а затем по области D.
, а затем по области D.
4.3.5. Для вычисления объема тела:
 .
.
4.3.6. Вычисление объема тела в цилиндрической системе координат 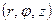 . Связь между цилиндрической и декартовой системой координат, если полюс и начало декартовой системы координат совмещены, а полярная ось идет по оси ох:
. Связь между цилиндрической и декартовой системой координат, если полюс и начало декартовой системы координат совмещены, а полярная ось идет по оси ох:  ,
, 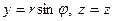 .
.
Элемент объема  ;
;  .
.
Примеры решения контрольных заданий
Пример 1.  ,
,
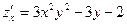 ;
;  ;
;  ;
; 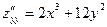
 ;
;  .
.  .
.
Пример 2. Дана функция  , точка
, точка 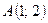 и
и  ,
, 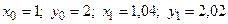 . Найти:
. Найти:
2а) полный дифференциал  при переходе из точки А в точку В.
при переходе из точки А в точку В.
2б) составить уравнение касательной плоскости к поверхности  в точке
в точке  , где
, где 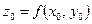 .
.
Решение.
2а) Найдём приращение аргументов 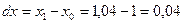 ;
; 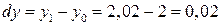 .
.  ;
; 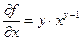 ;
; 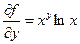 ;
;  ;
; 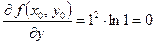 .
.
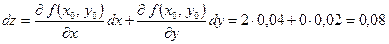 .
.
2б)  ;
; 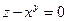 .
.
 ;
;  ;
; 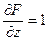 ;
;  .
.
 ;
; 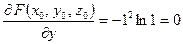 .
.
Уравнение касательной плоскости в точке  по 2.2
по 2.2
 , т.е.
, т.е.  или
или 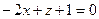 .
.
Пример 3. Вычислить с помощью двойного интеграла в полярных координатах площадь фигуры, ограниченной кривой, заданной уравнением в декартовых координатах 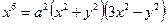
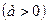 .
.
Решение: Переведем уравнение кривой в полярные координаты  ,
,  ,
,  . Тогда
. Тогда 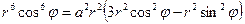 ,
, 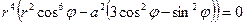 ,
,  ,
, 
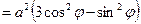 .
.  – это полюс. Уравнение границы области:
– это полюс. Уравнение границы области:  . Это выражение имеет смысл при
. Это выражение имеет смысл при  ;
; 
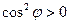 , (т.к. при
, (т.к. при 
 , получим
, получим  , что не имеет смысла). Тогда
, что не имеет смысла). Тогда 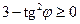 или
или  , т.е.
, т.е.  , т.е.
, т.е.  и
и  .
.  . Учтем формулы приведения
. Учтем формулы приведения  ,
,  и четность функций
и четность функций  ,
,  , поэтому
, поэтому  , где
, где  вычисляем при изменении
вычисляем при изменении  от 0 до
от 0 до  . По формуле 3.2.3 б)
. По формуле 3.2.3 б)
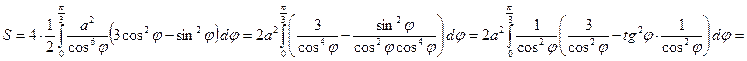

 .
.
Пример 4. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями  .
.
I.  – плоскость
– плоскость  ;
;
II.  – параболический цилиндр с образующей, параллельной оси у;
– параболический цилиндр с образующей, параллельной оси у;
III.  – параболический цилиндр с образующей, параллельной оси z;
– параболический цилиндр с образующей, параллельной оси z;
IV.  – параболический цилиндр с образующей, параллельной оси z.
– параболический цилиндр с образующей, параллельной оси z.
|
 находится между поверхностями III и IV, снизу ограничена плоскостью
находится между поверхностями III и IV, снизу ограничена плоскостью  (I), сверху накрыта поверхностью II.
(I), сверху накрыта поверхностью II.
 |
– 
 |
|


 .
На плоскости
.
На плоскости 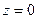 область D:
область D:
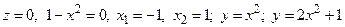 .
.


 куб. ед.
куб. ед.