5 контрольных заданий:
1. Дана функция  , точка
, точка  и вектор
и вектор  . Найти:
. Найти:
1)  в точке
в точке  ;
;
2) производную в точке  по направлению вектора
по направлению вектора  .
.
2. Дана кривая 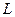 . С помощью криволинейных интегралов:
. С помощью криволинейных интегралов:
а) вычислить массу  отрезка кривой
отрезка кривой 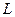 от точки
от точки  до точки
до точки  , если
, если
задана плотность  .
.
б) вычислить работу силы  при перемещении точки по кри-
при перемещении точки по кри-
вой от точки  до точки
до точки  .
.
3. На поверхности  , отсекаемой координатными плоскостями, распределен электричес-
, отсекаемой координатными плоскостями, распределен электричес-
кий заряд с плотностью  . Вычислить суммарный заряд поверхности.
. Вычислить суммарный заряд поверхности.
4.Даны векторное поле  и плоскость
и плоскость 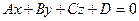 (р), которая совместно с координатными плоскостями образует пирамиду
(р), которая совместно с координатными плоскостями образует пирамиду  . Пусть
. Пусть  – основание пирамиды, принадлежащее плоскости (р),
– основание пирамиды, принадлежащее плоскости (р), 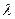 – контур, ограничивающий
– контур, ограничивающий  ;
;  – нормаль к
– нормаль к  , направленная вне пирамиды
, направленная вне пирамиды  . Требуется вычислить:
. Требуется вычислить:
1) Поток вектора  через поверхность
через поверхность  в направлении нормали
в направлении нормали  ;
;
2) Циркуляцию векторного поля  по замкнутому контуру
по замкнутому контуру 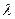 непосредственно и применив теорему Стокса к контуру
непосредственно и применив теорему Стокса к контуру 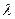 и ограниченной им поверхности
и ограниченной им поверхности  с нормалью
с нормалью  .
.
3) Поток векторного поля  через полную поверхность пирамиды
через полную поверхность пирамиды  в направлении внешней нормали к её поверхности непосредственно и применив теорему Гаусса-Остроградского. Сделать чертёж.
в направлении внешней нормали к её поверхности непосредственно и применив теорему Гаусса-Остроградского. Сделать чертёж.
5.Проверить, является ли векторное поле  потенциальным или соленоидальным. В случае потенциальности поля
потенциальным или соленоидальным. В случае потенциальности поля  найти его потенциал.
найти его потенциал.
| № вар-та | Задания |
| 1. | 1)  2)
2) 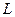 : окружность : окружность  . . 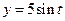 ; от ; от  , против часовой стрелки до , против часовой стрелки до  ; ;
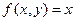 ; ;  .
3) .
3) 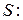  ; ;  .
4) .
4)  .
5) .
5) 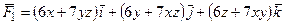 . .
|
| 2. | 1)  2)
2) 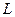 : отрезок прямой : отрезок прямой 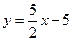 ; ;  ; ; 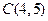 ; ;  ; ;
 .
3) .
3) 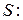  ; ;  .
4) .
4) 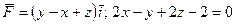 .
5) .
5)  . .
|
| 3. | 1)  2)
2) 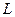 : отрезок прямой : отрезок прямой  ; ; 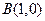 , , 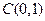 ; ;
 ; ;  .
3) .
3) 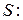  ; ;  .
4) .
4)  .
5) .
5)  . .
|
| 4. | 1)  2)
2) 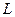 : парабола : парабола  ; ;  , ,  ; ;  ; ;  .
3) .
3) 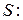  ; ;  .
4) .
4) 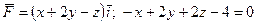 .
5) .
5)  . .
|
| 5. | 1) 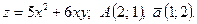 2)
2) 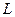 : эллипс : эллипс  , , 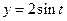 ; от ; от  до до  против часовой стрелки против часовой стрелки
 ; ;  .
3) .
3) 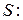  ; ;  .
4) .
4)  .
5) .
5)  . .
|
| 6. | 1)  2)
2) 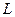 : отрезок прямой : отрезок прямой  ; ;  , ,  ; ;  ; ;  .
3) .
3) 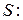  ; ; 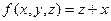 .
4) .
4)  .
5) .
5)  . .
|
| 7. | 1)  2)
2) 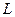 : кривая : кривая  ; ;  , ,  ; ;  ; ;  .
3) .
3) 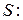  ; ;  .
4) .
4)  .
5) .
5)  . .
|
| 8. | 1) 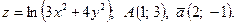 2)
2) 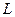 : отрезок прямой : отрезок прямой 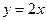 ; ;  , ,  ; ;  ; ;  .
3) .
3) 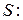  ; ;  .
4) .
4)  .
5) .
5)  . .
|
| 9. | 1)  2)
2) 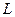 : отрезок прямой : отрезок прямой  ; ;  , ,  ; ;  ; ;
 .
3) .
3) 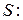  ; ;  .
4) .
4)  .
5) .
5)  . .
|
| 10. | 1)  2)
2) 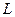 : кривая : кривая  ; ;  , , 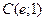 ; ;  ; ;  .
3) .
3) 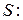  ; ;  .
4) .
4)  .
5) .
5) 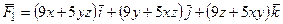 . .
|
|
Тема: «Ряды»
Краткая теория.
1. Числовые ряды
1.0)  , Число
, Число  – общий или n -ый член ряда.
– общий или n -ый член ряда.
1.1) Сумма ряда. Пусть  ,
, 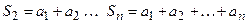 .
.  называется n -ой частной суммой. Если существует
называется n -ой частной суммой. Если существует  , то ряд называется сходящимся, а число S – суммой ряда. Иначе ряд – расходящийся.
, то ряд называется сходящимся, а число S – суммой ряда. Иначе ряд – расходящийся.
1.2)  ;
;  – остаток ряда. Если
– остаток ряда. Если  , то
, то  .
.
1.3) Необходимый признак сходимости ряда. Если ряд 1.0) сходится, то  . Применяется для доказательства расходимости ряда, таким образом:
. Применяется для доказательства расходимости ряда, таким образом:
1.3.1) Если  , то ряд
, то ряд  расходится.
расходится.
1.4) Знакоположительные ряды:  ,
,  .
.
Достаточные признаки сходимости:
1.4.1) Признаки сравнения.
Даны ряды (1)  и (2)
и (2) 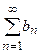 .
.
1.4.1.2 – 1.4.1.3) Пусть  , начиная с
, начиная с  , где N = любое натуральное число.
, где N = любое натуральное число.
Если ряд 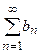 сходится, то ряд
сходится, то ряд  сходится.
сходится.
Если ряд  расходится, то ряд
расходится, то ряд 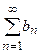 расходится.
расходится.
1.4.1.4.) Если  , то ряды
, то ряды  и
и 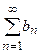 сходятся и расходятся одновременно.
сходятся и расходятся одновременно.
1.4.2) Интегральный признак Коши.
Дан ряд  ,
,  . Пусть
. Пусть  – монотонно убывающая функция, т.е.
– монотонно убывающая функция, т.е.  , тогда если: а)
, тогда если: а) 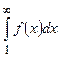 сходится, то
сходится, то  сходится; б)
сходится; б) 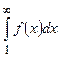 расходится, то
расходится, то  расходится.
расходится.
1.4.3) Признак Даламбера.
Дан ряд  . Пусть
. Пусть  .
.
При  .
.
1.4.4) Радикальный признак Коши.
Дан ряд  . Пусть
. Пусть 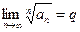 . При
. При  .
.
1.5) Знакочередующиеся ряды.
1.5.0) Ряд  , где
, где  .
.
1.5.1) Признак Лейбница.
Пусть а)  , (
, (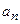 – монотонно убывают); б)
– монотонно убывают); б)  , тогда ряд
, тогда ряд  сходится и его сумма
сходится и его сумма  .
.
1.5.2) Следствие: Остаток ряда  . Если ряд
. Если ряд  сходится, то
сходится, то  . Остаток ряда по абсолютной величине меньше первого члена остатка.
. Остаток ряда по абсолютной величине меньше первого члена остатка.
1.6) Знакопеременный ряд.  , где
, где  имеют разные знаки.
имеют разные знаки.
1.7) Если ряд из абсолютных величин членов ряда  сходится, то ряд
сходится, то ряд  сходится абсолютно.
сходится абсолютно.
1.8) Если ряд  расходится, а ряд
расходится, а ряд  сходится, то говорят, что ряд
сходится, то говорят, что ряд  сходится условно.
сходится условно.
1.9) Знакочередующиеся ряды являются частным случаем знакопеременных рядов, поэтому, если для знакочередующегося ряда ряд из абсолютных величин  расходится, то надо применить признак Лейбница, чтобы проверить, сходится ли исходный ряд условно.
расходится, то надо применить признак Лейбница, чтобы проверить, сходится ли исходный ряд условно.
2. Степенные ряды
2.1)  ; Числа
; Числа 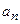 – коэффициенты ряда. При
– коэффициенты ряда. При  ряд
ряд  сходится,
сходится,  называется центром сходимости.
называется центром сходимости.
2.1.1) При  имеем ряд по степеням х:
имеем ряд по степеням х:  .
.
Заменой  ряд 2.1) приводится к виду 2.1.1)
ряд 2.1) приводится к виду 2.1.1) 
2.2) Радиусом сходимости степенного ряда называется такое число R, что при всех х, таких, что  степенной ряд абсолютно сходится, а для всех х, таких, что
степенной ряд абсолютно сходится, а для всех х, таких, что  степенной ряд расходится. Интервал
степенной ряд расходится. Интервал  называется интервалом сходимости. При
называется интервалом сходимости. При 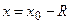 и
и 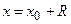 ряд может сходиться или расходиться. Это необходимо исследовать по признакам 1.3.1), 1.4.1), 1.4.2). Для рядов, расходящихся при всех х, кроме
ряд может сходиться или расходиться. Это необходимо исследовать по признакам 1.3.1), 1.4.1), 1.4.2). Для рядов, расходящихся при всех х, кроме  , радиус сходимости
, радиус сходимости  , а для рядов, сходящихся при всех х,радиус сходимости
, а для рядов, сходящихся при всех х,радиус сходимости  .
.
2.3) План нахождения интервала сходимости и радиуса сходимости  .
.
2.3.0) Дан ряд 
2.3.1) Составим ряд из абсолютных величин членов ряда 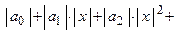
 Интервалы сходимости рядов 2.3.0) и 2.3.1) одинаковы.
Интервалы сходимости рядов 2.3.0) и 2.3.1) одинаковы.
2.3.2) К ряду 2.3.1), все члены которого положительны, можно применить признак Даламбера или радикальный признак Коши.
Применение признака Даламбера:  . В точках х, в которых этот предел меньше 1, ряд сходится, а в которых он больше 1, ряд расходится, значение
. В точках х, в которых этот предел меньше 1, ряд сходится, а в которых он больше 1, ряд расходится, значение  , при котором это предел равен 1, является значением радиуса сходимости
, при котором это предел равен 1, является значением радиуса сходимости  . Вид предела для определения интервала сходимости при применении радикального признака Коши
. Вид предела для определения интервала сходимости при применении радикального признака Коши  .
.
2.3.3) Исследуем сходимость числовых рядов на границах интервала сходимости по признакам 1.3.1), 1.4.1) или 1.4.2).
3. Разложение функции в степенные ряды.
3.1) Ряд Тейлора в окрестности 

 – значение n -ой производной функции
– значение n -ой производной функции  в точке
в точке  . Если
. Если  , то разложение по степеням х называется рядом Маклорена.
, то разложение по степеням х называется рядом Маклорена.
Таблица рядов Маклорена  в окрестности
в окрестности  ,
,  – функция от х,
– функция от х, 
| № | Ряд | Интервал сходимости |

| 
| |

| 
| |

| 
| |

| 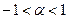
| |

| 
| |

| 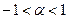
| |

| 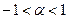
| |

| 
| |

| 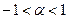
| |

| 
|
4. Применение рядов Тейлора
4.1) Вычисление определённых интегралов с помощью разложения функции в степенной ряд и затем интегрирования его почленно.
4.2) Решение дифференциальных уравнений.
Задано дифференциальное уравнение  и начальные условия в точке х = 0. Предположим, что в окрестности х = 0 решение уравнения можно разложить в степенной ряд
и начальные условия в точке х = 0. Предположим, что в окрестности х = 0 решение уравнения можно разложить в степенной ряд 
а) Этот ряд можно почленно дифференцировать столько, сколько надо, внутри интервала сходимости.
или б) Можно продифференцировать уравнение несколько раз, рассматривая у как функцию от х.
5. Разложение функции в ряд Фурье
5.1) Если  задана на
задана на  , то ряд Фурье для
, то ряд Фурье для  :
:
 , где
, где  .
.
Сумма ряда Фурье – периодическая функция с периодом  .
.
5.2) Если  – четная функция, то
– четная функция, то  , где
, где  .
.
5.3) Если  – нечетная функция, то
– нечетная функция, то 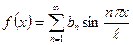 , где
, где  .
.