Определение. Целое неотрицательное число k называют суммой целых неотрицательных чисел m и p, если существуют непересекающиеся представители чисел m и p, объединение которых является представителем числа k.
Обозначают m + p, то есть k = m + p 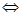 (
(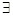 Am, Ap)[ Am
Am, Ap)[ Am 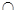 Ap =
Ap = 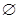
 Am
Am  Ap = Ak].
Ap = Ak].
Теорема.Сумма целых неотрицательных чисел не зависит от выбора их представителей.
Доказательство. Пусть множества Аm,Ap,Bm,Bp представители произвольных чисел m и p, причем
Am 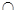 Ap=Bm
Ap=Bm 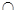 Bp=
Bp= 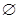 . Так как Am~ Bm
. Так как Am~ Bm  Ap ~ Bp
Ap ~ Bp  Am
Am  Ap ~ Bm
Ap ~ Bm  Bp. Если Am
Bp. Если Am  Ap
Ap  k
k  Bm
Bm  Bp
Bp  k, то есть сумма m + p, по определению равная k, не зависит от выбора представителей чисел m и p.
k, то есть сумма m + p, по определению равная k, не зависит от выбора представителей чисел m и p.
Теорема.Сумма целых неотрицательных чисел существует и единственна, то есть
( m, p
m, p  N0)(
N0)(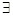 !k
!k  N0)[k = m + p].
N0)[k = m + p].
Доказательство. Докажем теорему о существовании и единственности суммы. Пусть m, p — произвольные целые неотрицательные числа, Am и Ap — их непересекающиеся представители. Так как множества Am и Ap — конечные, то их объединение Am  Ap так же конечное множество из цепочки
Ap так же конечное множество из цепочки 
 Am
Am  Ap находится в некотором классе k разбиения множества М / ~, причем только в нем одном, то есть Am
Ap находится в некотором классе k разбиения множества М / ~, причем только в нем одном, то есть Am  Ap — представитель числа k
Ap — представитель числа k  по определению суммы целых неотрицательных чисел число k — сумма чисел m и p.
по определению суммы целых неотрицательных чисел число k — сумма чисел m и p.
Поскольку класс, в котором находится объединение множеств Am и Ap единственный, то и сумма чисел m и p единственная. Таким образом, для любых произвольных чисел m и p существует единственное число k, являющееся их суммой.
Определение. Сложением целых неотрицательных чисел называют определенную на множестве N0 бинарную операцию, в которой образом пары чисел m и p является их сумма — число k. При этом компоненты пары называются слагаемыми.
Сложение целое неотрицательное число ассоциативно, то есть ( m, p, k
m, p, k  N0)[(m + p) + k = m + (p + k)].
N0)[(m + p) + k = m + (p + k)].
Пусть m, p, k — произвольные целые неотрицательные числа, Am, Ap, Ak — их попарно непересекающиеся представители, то есть Am 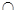 Ap =
Ap = 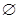 , Ap
, Ap 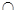 Ak=
Ak= 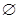 , Am
, Am 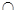 Ak=
Ak= 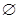 . Так как для любых m, p, k
. Так как для любых m, p, k  N0 по определению объединения их непересекающихся представителей имеет место (Am
N0 по определению объединения их непересекающихся представителей имеет место (Am  Ap)
Ap)  Ak = Am
Ak = Am  (Ap
(Ap  Ak),
Ak),
то (m + p) + k = m + (p + k).
Или через количественную характеристику множеств:
(а + в) + с = а + (в + с) 
 а = n (А), в = n (В), с = n (С), то по определению суммы двух чисел имеем:
а = n (А), в = n (В), с = n (С), то по определению суммы двух чисел имеем:
а + в = n (А  В), в + с = n (В
В), в + с = n (В  С)
С)  (а + в) + с = n ((А
(а + в) + с = n ((А  В)
В)  С).
С).
Так как объединение множеств ассоциативно, то (А  В)
В)  С=А
С=А  (В
(В  С)
С) 
 n((А
n((А  В)
В)  С)=n(А
С)=n(А  (В
(В  С)), то по определению суммы двух чисел имеем: n (А
С)), то по определению суммы двух чисел имеем: n (А  (В
(В  С)) = а + (в + с).
С)) = а + (в + с).
Таким образом, ( а, в, с
а, в, с  N0)[(а + в) + с = а + (в + с)].
N0)[(а + в) + с = а + (в + с)].
Рассмотрим свойства операции сложения на множестве натуральных чисел.
Свойство 1. Существует нейтральный элемент сложения, это число 0, т.е. ( )[m +0=m]
)[m +0=m]
Свойство 2.Сложение целых неотрицательных чисел коммутативно: ( m, p
m, p  N0)[m + p = p + m]
N0)[m + p = p + m]
Доказательство. Пусть m, p — произвольные целые неотрицательные числа, Аm и Аp — их непересекающиеся представители. Так как ( m, p
m, p  N0)(
N0)(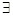 !k
!k  N0)[k = m + p] по теореме о существовании и единственности суммы, то
N0)[k = m + p] по теореме о существовании и единственности суммы, то
(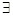 Am, Ap)[ Am
Am, Ap)[ Am 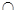 Ap =
Ap = 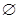
 Am
Am  Ap = Ak] по определению суммы.
Ap = Ak] по определению суммы.
Так как объединение множеств коммутативно, то
(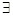 Ap, Am)[ Ap
Ap, Am)[ Ap 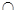 Am =
Am = 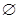
 Ap
Ap  Apm = Ak]
Apm = Ak]  p + m = k (по определению суммы).
p + m = k (по определению суммы).
Итак, m + p = k  p + m = k
p + m = k  по симметричности отношения «равно»
по симметричности отношения «равно»
m + p = k  k = p + m
k = p + m  по транзитивности отношения «равно»
по транзитивности отношения «равно»
m+ p = p + m  (
( m, p
m, p  N0)[m + p =p +m ].
N0)[m + p =p +m ].
Из теоремы существования и единственности суммы следует, что:
( m, p
m, p  N0´ N0)(
N0´ N0)(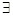 ! k
! k  N0)[m + p = k], то есть операция нахождения суммы целых неотрицательных чисел есть бинарная операция на множестве N0.
N0)[m + p = k], то есть операция нахождения суммы целых неотрицательных чисел есть бинарная операция на множестве N0.
Свойство 3. Сложение целых неотрицательных чисел монотонно относительно отношений «равно», «меньше», «больше».
Монотонность операции сложения относительно отношения «равно»:
(  m, p, k
m, p, k  N0)[m = p
N0)[m = p  m + k = p + k].
m + k = p + k].
Монотонность операции сложения относительно отношения «меньше»:
(  m, p, k
m, p, k  N0)[m<p
N0)[m<p  m+k <p + k].
m+k <p + k].
Монотонность сложения относительно отношения «больше»:
(  m, p, k
m, p, k  N0)[m > p
N0)[m > p  m + k >p + k].
m + k >p + k].
Свойство 4. Операция сложение целых неотрицательных чисел сократимо относительно отношений «равно», «меньше», «больше».
Сократимость операции сложения относительно отношения «равно»:
(  m, p, k
m, p, k  N0)[ m + k = p + k
N0)[ m + k = p + k  m =p].
m =p].
Сократимость операции сложения относительно отношения «<»: ( m, p, k
m, p, k  N0)[m + k< p + k
N0)[m + k< p + k  m < p].
m < p].
Сократимость операции сложения относительно отношения «больше»: ( m, p, k
m, p, k  N0) [ m + k > p + k
N0) [ m + k > p + k  m > p].
m > p].
Определение. Целое неотрицательное число k называют разностью целых неотрицательных чисел m и p, если дополнение некоторого представителя числа m является представителем числа k. Обозначают: m — p.
Из определения разности целых неотрицательных чисел следует:
k = m — p 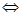
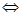 (
(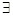 Am, Ap)[Ap
Am, Ap)[Ap 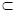 Am
Am  Am\Ap = Ak]
Am\Ap = Ak]
Теорема о связи между разностью и суммой. Разность чисел m и p равна числу k тогда и только тогда, когда число m равно сумме чисел p и k.
m — p = k 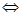 (
(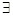 Am, Ap)[Ap
Am, Ap)[Ap 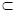 Am
Am  Am\Ap = Ak] (по определению разности)
Am\Ap = Ak] (по определению разности) 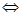
(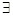 Ap, Аk)[Ap
Ap, Аk)[Ap 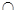 Ak =
Ak = 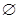
 Ap
Ap  Ak = Am]
Ak = Am] 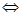 m = p + k (определение суммы).
m = p + k (определение суммы).
Теорема о существовании и единственности разности. Разность целых неотрицательных чисел существует тогда и только тогда, когда m > p 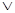 m = p. Если разность существует, то она единственна.
m = p. Если разность существует, то она единственна.
Доказательство. Докажем теорему о существовании и единственности разности. Пусть m, p — произвольные целые неотрицательные числа. Докажем необходимое и достаточное условия существования разности, то есть докажем, что (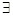 k
k  N0)[k = m — p
N0)[k = m — p 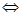 m
m 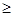 p].
p].
Имеем: k = m — p  m — p = k
m — p = k  m = p + k
m = p + k  (по определению отношения «меньше») m > p
(по определению отношения «меньше») m > p 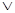 m = p.
m = p.
Докажем единственность разности методом от противного. Предположим, что разность не единственна, то есть, что m — p = k  m — p = t
m — p = t  k
k 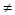 t. Имеем: m — p = k
t. Имеем: m — p = k  m — p = t
m — p = t  m = p + k
m = p + k  m = p + t
m = p + t  p + k = p + t
p + k = p + t  (по сократимости сложения относительно отношения «равно») k = t
(по сократимости сложения относительно отношения «равно») k = t  (m — p = k
(m — p = k  m — p = t)
m — p = t)  Л. Следовательноразность единственна.
Л. Следовательноразность единственна.
Определение. Вычитанием целых неотрицательных чисел называют частично определенная на множестве N0 бинарная операция, в которой образом пары (m, p), находящейся в отношении «больше» или«равно», является разность m — p. Первый компонент пары называется уменьшаемым, второй — вычитаемым.
Рассмотрим свойства операции вычитания.
Свойство 1. Существование нейтрального элемента:
( m
m  N0)[m — 0 = m] — 0 — нейтральный элемент при вычитании.
N0)[m — 0 = m] — 0 — нейтральный элемент при вычитании.
Свойство 2. Для операции вычитания имеет место «самонейтрализация»
( m
m  N0)[m — m = 0].
N0)[m — m = 0].
Свойство 3. Вычитание монотонно относительно отношений «равно», «меньше», «больше»:
Доказательство. Монотонность операции вычитания относительно отношения «равно»:
(  m, p, k
m, p, k  N0)[m = p
N0)[m = p  k
k 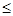 m
m  m — k = p — k].
m — k = p — k].
Докажем монотонность операции вычитания относительно отношения «равно». Пусть m, p, k — произвольные целые неотрицательные числа. По условию m=p  m=k+t
m=k+t  p=k + t
p=k + t  p— k=t.
p— k=t.
Имеем: m — k = t  p — k = t
p — k = t  m — k = p — k.
m — k = p — k.
Доказательство. Монотонность операции вычитания относительно отношения «меньше»:
(  m, p, k
m, p, k  N0)[m < p
N0)[m < p  k
k 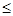 m
m  m — k < p — k].
m — k < p — k].
Докажем монотонность операции вычитания относительно отношения «меньше».
По условию m < p  (
(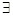 t
t  N)[p = m + t]. k
N)[p = m + t]. k 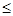 m
m  (
(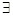 s
s  N0)[m = k + s]
N0)[m = k + s]  m — k = s.
m — k = s.
Имеем: p = m + t  m = k + s
m = k + s  p = (k + s) + t = k + (s + t)
p = (k + s) + t = k + (s + t)  p — k = s + t
p — k = s + t 
 s < p — k.
s < p — k.
Имеем: m — k = s  s < p — k
s < p — k  m — k < p — k.
m — k < p — k.
Доказательство. Монотонность операции вычитания относительно отношения «больше»:
(  m, p, k
m, p, k  N0)[m > p
N0)[m > p  k
k 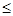 m
m  m — k > p — k].
m — k > p — k].
Докажем монотонность операции вычитания относительно отношения «больше».
По условию: m > p  p < m
p < m  (по монотонности относительно отношения «меньше») p — k < m — k (k
(по монотонности относительно отношения «меньше») p — k < m — k (k 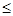 p)
p)  m — k > p — k.
m — k > p — k.
Свойство 4. Операция вычитания сократима относительно отношений «равно», «меньше», «больше».
Сократимость операции вычитания относительно отношения «равно»:
Сократимость операции вычитания относительно отношения «меньше»: ( m, p, k
m, p, k  N0)[ m — k < p — k
N0)[ m — k < p — k  m < p].
m < p].
Сократимость вычитания относительно отношения «больше»: ( m, p, k
m, p, k  N0)[m — k > p — k
N0)[m — k > p — k  m > p].
m > p].