ЕН. Ф. 01 МАТЕМАТИКА
Методические указания
и варианты заданий к контрольной работе № 1
Специальности: 250201 Лесное хозяйство
280402 Природоохранное обустройство территорий
Уфа 2009
УДК 51(07)
ББК 22.1я73,22.161.6
М 54
Рекомендовано к изданию методической комиссией факультета лесного хозяйства (протокол № 6 от 24.04.2009 года)
Составители: доцент, к.соц.н. Саитова Р.З.
доцент, к.физ.-мат.н. Маннанов М.М.
Рецензент: доцент кафедры физики Юмагужин Р.Ю.
Ответственный за выпуск: зав. кафедрой математики
доцент, к.физ.-мат.н. Лукманов Р.Л.
ВВЕДЕНИЕ
Целью настоящих методических указаний является помощь студентам в освоении и закреплении следующих разделов математики: линейная и векторная алгебра, аналитическая геометрия.
Расчетно-графическая работа № 1 состоит из 5 заданий. В каждом задании 30 вариантов. Номер варианта студент выбирает по формуле: № = a · b + c, где a – номер задания, b и с – предпоследняя и последняя цифры шифра (номера зачетной книжки или студенческого билета).
Например, номер студенческого билета (зачетки) студента 1265. Тогда в первом задании этот студент выполняет вариант:
№ = 1 · 6 + 5 = 11. Во втором задании: № = 2 · 6 + 5 = 17 и т.д. Если получается вариант больше 30, то нужно вычитать 30. Например, для этого же студента третье задание будет высчитываться: 5 · 6 + 5 = 35. Следовательно, этот студент решает 35 – 30 = 5 – пятый вариант третьего задания.
Прежде чем приступать к выполнению работы, целесообразно изучить соответствующие разделы в учебниках, рекомендованных в библиографическом списке.
ПРИМЕРЫРЕШЕНИЯ ЗАДАЧ
Задача 1
Й способ решения
Пусть требуется, используя формулы Крамера, решить систему

Подсчитаем сначала главный определитель системы ∆, воспользовавшись следующим правилом вычисления определителей третьего порядка:
 = а 11 ·
= а 11 · 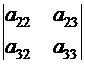 – а 12 ·
– а 12 ·  + а 13 ·
+ а 13 ·  .
.
У нас ∆ =  = 1 ∙ (1 – 12) + 2 ∙ (2 – 9) + 1 ∙ (8 – 3) = – 20.
= 1 ∙ (1 – 12) + 2 ∙ (2 – 9) + 1 ∙ (8 – 3) = – 20.
Так как ∆ ≠ 0, делаем вывод о том, что система имеет единственное решение. Для его отыскания вычислим вспомогательные определители ∆ x, ∆ y, ∆ z:
∆ x =  = 4 · (1 – 12) – (– 2) · (5 + 6) + 1 · (20 + 2) = 0,
= 4 · (1 – 12) – (– 2) · (5 + 6) + 1 · (20 + 2) = 0,
∆ y =  = 1 · (5 + 6) – 4 · (2 – 9) + 1 · (– 4 – 15) = 20,
= 1 · (5 + 6) – 4 · (2 – 9) + 1 · (– 4 – 15) = 20,
∆ z =  = 1 · (– 2 – 20) – (– 2) · (– 4 – 15) + 4 · (8 – 3) = – 40.
= 1 · (– 2 – 20) – (– 2) · (– 4 – 15) + 4 · (8 – 3) = – 40.
Далее, воспользовавшись формулами Крамера, окончательно получим
x =  = 0, y =
= 0, y =  = – 1, z =
= – 1, z = 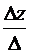 = 2.
= 2.
Всем трем равенствам они удовлетворяют, поэтому делаем вывод о правильности полученного решения: x = 0; y = – 1; z = 2.
Й способ решения
Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы:

Решение. Обозначим через А – матрицу коэффициентов при неизвестных; Х – матрицу-столбец неизвестных x, y, z и Н – матрицу-столбец свободных членов:
А =  , Х =
, Х = 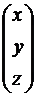 , Н =
, Н =  .
.
С учетом этих обозначений данная система уравнений принимает следующую матричную форму:
А · Х = Н. (1)
Если матрица А – невырожденная (ее определитель ∆ отличен от нуля), то она имеет обратную матрицу А –1. Умножив обе части уравнения (1) на А –1 слева, получим:
А –1 · А · Х = А –1 · Н.
Но А –1 · А = Е (Е – единичная матрица), а ЕХ = Х, поэтому
Х = А –1 · Н. (2)
Равенство (2) называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А –1.
Пусть имеем невырожденную матрицу
А =  . Тогда А –1 =
. Тогда А –1 =  ,
,
где Аij (i = 1, 2, 3; j = 1, 2, 3) – алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (– 1) i + j на минор (определитель) второго порядка, полученный вычеркиванием i -й строки j -го столбца в определителе матрицы А, т.е. Aij = (– 1) i + j · Mij.
Вычислим определитель ∆ и алгебраические дополнения Аij элементов матрицы А.
∆ =  = 10 ≠ 0, следовательно, матрица А имеет обратную матрицу А –1.
= 10 ≠ 0, следовательно, матрица А имеет обратную матрицу А –1.
А 11 = (– 1)1+1 ∙  = 5, А 21 = (– 1)2+1 ∙
= 5, А 21 = (– 1)2+1 ∙  = 3,
= 3,
А 12 = (– 1)1+2 ∙  = – 5, А 22 = (– 1)2+2 ∙
= – 5, А 22 = (– 1)2+2 ∙  = 1,
= 1,
А 13 = (– 1)1+3 ∙  = – 5, А 23 = (– 1)2+3 ∙
= – 5, А 23 = (– 1)2+3 ∙ 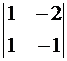 = – 1,
= – 1,
А 31 = (– 1)3+1 ∙  = – 1, А 32 = (– 1)3+2 ∙
= – 1, А 32 = (– 1)3+2 ∙  = 3,
= 3,
А 33 = (– 1)3+3 ∙  = 7.
= 7.
Тогда А –1 =  =
=  .
.
По формуле (2) находим решение данной системы уравнений
в матричной форме:
Х = А –1 · Н =  ·
·  ·
·  =
=
=  ·
·  =
=  ·
·  =
=  .
.
Отсюда x = 3, y = 0, z = – 2.
Й способ решения
Метод Гаусса
Решить систему уравнений: 
Составим расширенную матрицу системы:
 .
.
Разрешающим элементом а 11 удобно иметь единицу, поэтому переставим второе уравнение на место первого.
Получим нули в первом столбце, умножив первое уравнение последовательно на (– 2) и (– 3) и складывая со вторым и третьим.

 ~
~ 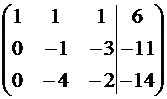 ~
~  .
.
С помощью второго элемента второй строки сделаем нуль
во втором столбце третьей строки, для чего умножим вторую строку на (– 2) и сложим с третьей.

 ~
~  ~
~  .
.
Таким образом, свели матрицу к треугольному виду. Запишем полученную систему уравнений:

Из последнего уравнения сразу находим значения z = 3, подставляя которое во второе уравнение находим y = 11 – 3 z = 11 – 9 = 2. Затем из первого уравнения найдем x = 6 – y – z = 6 – 2 – 3 = 1. Поэтому x = 1, y = 2, z = 3.
Задача 2
Даны вершины треугольника ABC: A (– 2, 5), B (10, – 4), C (8, 10). Требуется найти: 1) длину стороны AB; 2) уравнения сторон AB и AC в общем виде и их угловые коэффициенты; 3) угол A в радианах;
4) уравнение медианы AD; 5) уравнение высоты CE и ее длину;
6) уравнение окружности, для которой высота CE есть диаметр и точки пересечения этой окружности со стороной AC.
Решение.
1. Расстояние d между точками A (х 1; y 1) и B (х 2; y 2) вычисляем по формуле:
d =  (1)
(1)
Применяя (1), находим длину стороны AB:
dAB =  =
=  = 15.
= 15.
2. Уравнение прямой, проходящей через точки A (х 1; y 1) и B (х 2; y 2), имеет вид:
 . (2)
. (2)
Подставив в (2) соответствующие координаты точек A и B находим уравнение прямой (AB):
 =
=  ;
;  =
=  ;
;
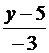 =
=  ; 4 y – 20 = – 3 x – 6; 3 x + 4 y – 14 = 0 (AB).
; 4 y – 20 = – 3 x – 6; 3 x + 4 y – 14 = 0 (AB).
Чтобы найти угловой коэффициент прямой AB (kAB), решим полученное уравнение прямой относительно y:
4 y = 3 x + 14,  откуда
откуда 
Подставляя в (2) координаты точек A и C, находим уравнения прямой (AC):



 откуда
откуда 
3. Если даны две прямые, угловые коэффициенты которых соответственно равны k 1 и k 2, то угол φ между этими прямыми определяется по формуле:
 . (3)
. (3)
Искомый угол A образован прямыми AB и AC, угловые коэффициенты которых найдены ранее в пункте 2. Для определения угла A положим 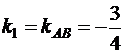 и
и  . Применяя (3), получим:
. Применяя (3), получим:
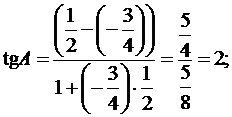 откуда
откуда  .
.
Используя таблицу перевода градусной меры в радианную, получим A = 1,107 рад.
4. Если AD есть медиана, то точка D является серединой стороны BC. Для вычисления координат точки D применяем формулы деления отрезка на две равные части:

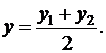 (4)
(4)
Подставив в (4) координаты точек B и C, находим координаты точки D:

 D (9; 3).
D (9; 3).
Подставив в (2) координаты точек A (– 2; 5) и D (9; 3), находим искомое уравнение медианы AD:
2 x + 11 y – 51 = 0 (AD).
5. Высота CE перпендикулярна стороне AB. Известно, что если две прямые взаимно перпендикулярны, то их угловые коэффициенты обратны по величине и противоположны по знаку. Следовательно,  . Так как
. Так как 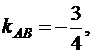 то
то 
Уравнение прямой, проходящей через данную точку, имеет вид:
 (5)
(5)
Подставив в (5) координаты точки C и найденный угловой коэффициент  , получим искомое уравнение высоты CE:
, получим искомое уравнение высоты CE:



Чтобы найти длину CE, определим сперва координаты точки E – точки пересечения высоты CE и прямой AB. Для этого решаем совместно систему уравнений (AB) и (CE):

Решение этой системы дает x = 2 и y = 2. Следовательно, E (2; 2). Длину высоты CE определяем как расстояние между двумя точками по формуле (1).
dCE =  = 10.
= 10.
6. Уравнение окружности с центром в точке K (a; b) и радиусом R имеет вид:
(x – a)2 + (y – b)2 = R 2. (6)
По условию, высота CE служит диаметром искомой окружности. Следовательно, центр окружности K является серединой отрезка CE. Используя (4), находим координаты точки K.
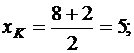
 K (5; 6).
K (5; 6).
Так как dCE = 10, то радиус окружности R = 5. Следовательно,
(x – 5)2 + (y – 6)2 = 25 – уравнение искомой окружности. Чтобы найти точки пересечения этой окружности с прямой AC, решаем совместную систему уравнений:

Решив эту систему, получим две точки пересечения C (8; 10) и М (0; 6). Треугольник ABC, медиана AD, высота CE, окружность с центром в точке K и точки ее пересечения со стороной AC построены в системе координат xOy на рис. 1.

Рисунок 1
Задача 3
На плоскости даны два вектора  = {2; – 3} и
= {2; – 3} и  = {1; 2}. Найти разложение вектора
= {1; 2}. Найти разложение вектора  = {9; 4} по базису
= {9; 4} по базису  и
и  .
.
Решение: Так как векторы  и
и  неколлинеарны, то вектор
неколлинеарны, то вектор  можно единственным образом выразить через эти векторы:
можно единственным образом выразить через эти векторы:  = m
= m  + n
+ n  . Это соотношение и называется разложением вектора
. Это соотношение и называется разложением вектора  по базису
по базису  и
и  . Надо найти числа m и n. Для этого проделаем следующее:
. Надо найти числа m и n. Для этого проделаем следующее:
 = 9
= 9  + 4
+ 4  ,
,  = 2
= 2  – 3
– 3  ,
,  =
=  + 2
+ 2  ,
,
тогда 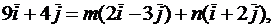

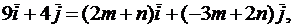
отсюда 

Окончательно,  = 2
= 2  + 5
+ 5  .
.
Задача 4
Даны координаты вершин А (0; 0; 1), В (2; 3; 5), С (6; 2; 3), D (3; 7; 2) пирамиды ABCD. Требуется:
1) записать векторы 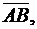

 в системе орт
в системе орт  ,
,  ,
, 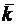 и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между векторами 
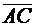 ;
;
3) найти проекцию вектора  на вектор
на вектор  ;
;
4) найти площадь грани ABC;
5) найти объем пирамиды ABCD;
6) составить уравнение ребра AC;
7) составить уравнение грани ABC.
1. Известно, что произвольный вектор  представляется в системе орт
представляется в системе орт  ,
,  ,
, 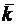 по формуле
по формуле
 = ax
= ax  + ay
+ ay  + az
+ az 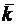 , (1)
, (1)
где ax, ay, az – координаты вектора  в системе координат, порожденной ортами, причем
в системе координат, порожденной ортами, причем
ax = npOx  , ay = npOy
, ay = npOy  , az = npOz
, az = npOz  .
.
Если заданы точки M 1(x 1, y 1, z 1), M 2(x 2, y 2, z 2), то для вектора
 =
=  .
.


 ,
,
то есть
 . (2)
. (2)
Воспользовавшись формулой (2) и координатами заданных точек А, В, С, D получим:



Если вектор  задан формулой (1), то его модуль вычисляется следующим образом:
задан формулой (1), то его модуль вычисляется следующим образом:
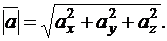 (3)
(3)
Используя формулу (3), получаем модули найденных векторов:
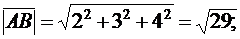


2. Известна формула cos  =
=  где
где  ·
·  – скалярное произведение векторов
– скалярное произведение векторов  и
и  , которое можно вычислить следующим образом:
, которое можно вычислить следующим образом:
 ·
·  =
=  .
.
У нас
cos φ = cos  =
= 
то есть  .
.
3. Известно, что
 ,
,
то есть в нашем случае

4. Воспользуемся формулой нахождения площади треугольника, построенного на векторах  и
и  :
:
 ,
,
где  – векторное произведение векторов, которое можно вычислить по следующему правилу:
– векторное произведение векторов, которое можно вычислить по следующему правилу:
 .
.
В нашем примере  , причем
, причем

Таким образом,
 (кв.ед.).
(кв.ед.).
5. Объем пирамиды, построенной на трех некомпланарных векторах  , можно найти по формуле
, можно найти по формуле

где  – смешанное произведение векторов, которое вычисляется следующим образом:
– смешанное произведение векторов, которое вычисляется следующим образом:
 .
.
У нас  где
где

то есть  (куб. ед.).
(куб. ед.).
6. Известно, что уравнение прямой, проходящей через две заданные точки пространства  и
и  , имеет вид:
, имеет вид:
 (4)
(4)
Подставив в (4) координаты точек A и C, получим

то есть уравнение ребра AC окончательно запишется следующим
образом:
 или
или  .
.
7. Уравнение плоскости, проходящей через три заданные точки 

 можно записать в виде:
можно записать в виде:
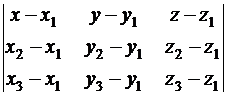 .
.
Подставляя в него координаты точек A, B, C, получим
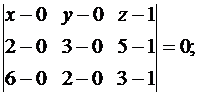



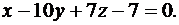
Задача 5
Составить уравнение геометрического места точек, отношение расстояний, которых до данной точки А (4; 0) и до данной прямой x = 1 равно 2.
Решение.
В системе координат xOy построим точку А(4; 0) и прямую х = 1.
Пусть М (х; у) – произвольная точка искомого геометрического места точек. Отпустим перпендикуляр МВ на данную прямую х = 1 и определим координаты точки В. Так как точка В лежит на заданной прямой, то ее абсцисса равна 1, ордината точки В равна ординате точки В. Следовательно, В (1; у)
По условию задачи, МА: МВ = 2. Расстояния МА и МВ находим по формуле

Тогда имеем:

Возведя в квадрат левую и правую части, получим:

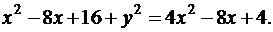
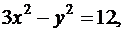 или
или 
Полученное уравнение представляет собой гиперболу, у которой действительная полуось равна 2, а мнимая равна  т.е.
т.е.
a = 2, b = 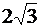 .
.
Определим фокусы гиперболы.
Для гиперболы выполняется равенство c 2 = a 2 + b 2. Следовательно, c 2 = 4 + 12 = 16, с = 4. F 1(– 4; 0), F 2(4; 0) – фокусы гиперболы. Заданная точка А (4; 0) является правым фокусом гиперболы.
Определим эксцентриситет полученной гиперболы:
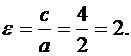
Уравнение асимптот гиперболы имеет вид  и
и  . Следовательно,
. Следовательно,  или
или  ,
,  – асимптоты гиперболы.
– асимптоты гиперболы.

Рисунок 2
РАСЧЕТНЫЕ ЗАДАНИЯ
Задание № 1
Решить систему линейных уравнений методом Крамера, Гаусса и матричным способом. Сделать проверку полученного решения.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11.  12.
12. 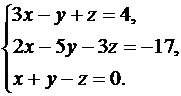
13.  14.
14. 
15.  16.
16. 
17.  18.
18. 
19. 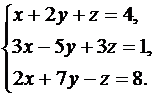 20.
20. 
21. 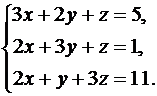 22.
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 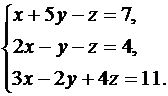
29.  30.
30. 
Задание № 2
1. Даны координаты вершин треугольника ABC. Требуется найти: 1) длину стороны AB; 2) уравнения сторон AB и AC в общем виде, их угловые коэффициенты; 3) угол A в радианах; 4) уравнение медианы AD; 5) уравнение высоты CE и ее длину; 6) уравнение окружности, для которой высота CE есть диаметр и точки пересечения этой окружности со стороной AC.
| № | А | В | С | № | A | B | C |
| 1. | (– 6; – 4) | (– 10; – 1) | (6; 1) | 16. | (0; – 1) | (12; 8) | (10; – 6) |
| 2. | (12; 0) | (18; 8) | (0; 5) | 17. | (– 6; 1) | (6; 10) | (4; – 4) |
| 3. | (– 2; – 6) | (– 6; – 3) | (10; – 1) | 18. | (– 2; – 4) | (10; 5) | (8; – 9) |
| 4. | (8; 2) | (14; 10) | (– 4; 7) | 19. | (– 3; 0) | (9; 9) | (7; – 5) |
| 5. | (2; – 4) | (– 2; – 1) | (14; 1) | 20. | (– 9; – 2) | (3; 7) | (1; – 7) |
| 6. | (2; – 1) | (8; 7) | (– 10; 4) | 21. | (– 5; 2) | (7; – 7) | (5; 7). |
| 7. | (5; – 3) | (1; 10) | (17; 2) | 22. | (– 7; 5) | (5; – 4) | (3; 10) |
| 8. | (14; – 6) | (20; 2) | (2; – 1) | 23. | (– 7; 1) | (5; – 8) | (3; 6) |
| 9. | (3; 4) | (– 1; 7) | (15; 9) | 24. | (0; 3) | (12; – 6) | (10; 8) |
| 10. | (1; – 2) | (7; 6) | (– 11; 3) | 25. | (– 8; 4) | (4; – 5) | (2; 9) |
| 11. | (– 5; 0) | (7; 9) | (5; – 5) | 26. | (– 2; 2) | (10; – 7) | (8; 7) |
| 12. | (– 7; 2) | (5; 11) | (3; – 3) | 27. | (1; 2) | (13; – 7) | (11; 7) |
| 13. | (– 5; – 3) | (7; 6) | (5; – 8) | 28. | (– 4; 1) | (8; – 8) | (6; 6) |
| 14. | (– 6; – 2) | (6; 7), | (4; – 7). | 29. | (– 7; – 1) | (– 5; – 10) | (3; 4) |
| 15. | (– 8; – 4), | (4; 5), | (2; – 9). | 30. | (– 3; 3) | (9; – 6) | (7; 8) |
Задание № 3
1. Даны векторы 
 ,
, 
 Показать, что векторы
Показать, что векторы 
 ,
,  образуют базис трехмерного пространства и найти координаты вектора
образуют базис трехмерного пространства и найти координаты вектора 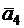 в этом базисе.
в этом базисе.
| № | 
| 
| 
| 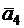
|
| 1. | {2, 0, 8} | {– 10, 3, 0} | {– 3, 5, 1} | {– 1, – 7, 9} |
| 2. | {1, 4, 0} | {– 5, 1, – 2} | {– 3, 1, – 3} | {2, – 7, 9} |
| 3. | {3, 7, 9} | {– 3, 0, 7} | {2, – 3, – 5} | {1, – 2, 0} |
| 4. | {– 1, 3, 5} | {5, – 1, 3} | {– 2, 9, – 2} | {8, 0, 1} |
| 5. | {5, 1, – 7} | {2, – 3, – 1} | {– 7, – 1, 1} | {3, 4, – 5} |
| 6. | {9, 7, 1} | {8, – 1, – 1} | {0, 5, 5} | {0, 0, 4} |
| 7. | {2, 9, 0} | {– 4, – 7, – 1} | {1, – 2, 5} | {3, 4, 0} |
| 8. | {1, 9, 0} | {– 3, – 2, 0} | {– 5, – 6, – 8} | {– 7, 0, 1} |
| 9. | {– 1, 5, 2} | {– 3, 3, – 7} | {5, – 2, 0} | {2, – 4, 0} |
| 10. | {8, 5, 9,} | {1, – 3, – 6} | {3, – 1, 5} | {0, 2, – 1} |
| 11. | {1, 2, 3} | {2, 1, 2} | {3, 2, 1} | {1, 1, 1} |
| 12. | {2, – 3, 5} | {1, 2, 3} | {3, – 1, – 2} | {– 1, 3, 5} |
| 13. | {2, – 3, 1} | {1, 2, 7} | {3, – 1, 5} | {0, 4, 1} |
| 14. | {1, 2, 3} | {2, 1, 4} | {– 1, 2, 5} | {1, 2, 8} |
| 15. | {3, – 1, 0} | {– 2, 1, 1} | {2, – 1, 4} | {2, 2, 2} |
| 16. | {1, – 8, 3} | {2, 1, 1} | {4, 7, – 4} | {1, 2, 1} |
| 17. | {5, – 1, 7} | {2, 1, 1} | {1, – 3, 0} | {3, – 6, 1} |
| 18. | {1, 2, 5} | {1, – 1, 3} | {3, – 6, – 1} | {1, 2, – 7} |
| 19. | {1, 2, 3} | {– 1, 3, 2} | {7, – 3, 5} | {6, 10, 17} |
| 20. | {4, 7, 8} | {9, 1, 3} | {2, – 4, 1} | {1, – 13, – 13} |
| 21. | {2; 1; 3} | {3; – 2; 1} | {1; – 3; – 4} | {7; 0; 7} |
| 22. | {5; 3; 1} | {– 2; – 1; 2} | {– 2; 1; 4} | {3; 0; 1} |
| 23. | {1; 3; 5} | {– 2; – 1; – 1} | {4; – 2; 4} | {– 7; 3; – 1} |
| 24. | {3; 1; 6} | {– 2; 2; – 3} | {– 4; 5; – 1} | {3; 0; 1} |
| 25. | {4; 1; 4} | {– 2; – 1; – 1} | {– 3; 1; 5} | {– 3; – 2; 1} |
Продолжение таблицы
| № | 
| 
| 
| 
|
| 26. | {1; 2; 5} | {2; – 3; 4} | {1; – 1; – 2} | {3; 0; 1} |
| 27. | {5; 1; 2} | {3; 4; – 1} | {– 4; 2; 1} | {– 3; 5; 4} |
| 28. | {2; 1; 5} | {– 4; 3; 5} | {1; – 1; – 4} | {4; – 1; – 3} |
| 29. | {3; 1; 4} | {– 4; 2; 3} | {2; – 1; – 2} | {– 7; – 1; 0} |
| 30. | {1; 4; 2} | {5; – 2; – 3} | {– 2; – 1; 1} | {– 3; 2; 4} |
Задание № 4
Даны координаты вершин пирамиды ABCD. Требуется:
1) записать векторы 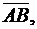

 в системе орт
в системе орт 
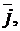
 и найти модули этих векторов;
и найти модули этих векторов;
2) найти угол между векторами 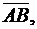
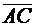 ;
;
3) найти проекцию вектора  на вектор
на вектор  ;
;
4) найти площадь грани ABC;
5) найти объем пирамиды ABCD;
6) составить уравнение ребра AC;
7) составить уравнение грани ABC.
| № | A | B | C | D |
| 1. | {1; 2; 1} | {– 1; 5; 1} | {– 1:2; 7} | {1; 5; 9} |
| 2. | {2; 3; 2} | {0; 6; 2} | {0; 3; 8} | {2; 6; 10} |
| 3. | {0; 3; 2} | {– 2:6; 2} | {– 2; 3; 8} | {0; 6; 10} |
| 4. | {2; 1; 2} | {0; 4; 2} | {0; 1; 8} | {2; 4; 10} |
| 5. | {2; 3; 0} | {0; 6; 0} | {0; 3; 6} | {2; 6; 8} |
| 6. | {2; 2; 1} | {0; 5; 1} | {0; 2; 7} | {2; 5; 9} |
| 7. | {1; 3; 1} | {– 1; 6; 1} | {– 1; 3; 7} | {1; 6; 9} |
| 8. | {1; 2; 2} | {– 1; 5; 2} | {– 1; 2; 8} | {1; 5; 10} |
| 9. | {2; 3; 1} | {0; 6; 1} | {0; 3; 7} | {2; 6; 9} |
| 10. | {2; 2; 2} | {0; 5; 2} | {0; 2; 8} | {2; 5; 10} |
| 11. | {1; 3; 2} | {– 1; 6; 2} | {– 1; 3; 8} | {1; 6; 10} |
| 12. | {0; 1; 2} | {– 2:4; 2} | {– 2; 1; 8} | {0; 4; 10} |
| 13. | {0; 3; 0} | {– 2; 6; 0} | {– 2; 3; 6} | {0; 6; 8} |
| 14. | {2; 1; 0} | {0; 4; 0} | {0; 1; 6} | {2; 4; 8} |
| 15. | {0; 2; 1} | {– 2; 5; 1} | {– 2; 2; 7} | {0; 5; 9} |
| 16. | {1; 1; 1} | {– 1; 4; 1} | {– 1; 1; 7} | {1; 4; 9} |
| 17. | {1; 2; 0} | {– 1; 5; 0} | {– 1; 2; 6} | {1; 5; 8} |
| 18. | {0; 1; 0} | {– 2; 4; 0} | {– 2; 1; 6} | {0; 4; 8} |
| 19. | {0; 1; 1} | {– 2; 4; 1} | {– 2; 1; 7} | {0; 4; 9} |
| 20. | {0; 2; 0} | {– 2; 5; 0} | {– 2; 2; 6} | {0; 5; 8} |
| 21. | {4; 2; 5} | {0; 7; 2} | {0; 2; 7} | {1; 5; 0} |
| 22. | {4; 4; 10} | {4; 10; 2} | {2; 8; 4} | {9; 6; 4} |
| 23. | {4; 6; 5} | {6; 9; 4} | {2; 10; 10} | {7; 5; 9} |
| 24. | {3; 5; 4} | {8; 7; 4} | {5; 10; 4} | {4; 7; 8} |
| 25. | {10; 6; 6} | {– 2; 8; 2} | {6; 8; 9} | {7; 10; 3} |
| 26. | {1; 8; 2} | {5; 2; 6} | {5; 7; 4} | {4; 10; 9} |
| 27. | {6; 6; 5} | {4; 9; 5} | {4; 6; 11} | {6; 9; 3} |
| 28. | {7; 2; 2} | {5; 7; 7} | {5; 3; 1} | {2; 3; 7} |
| 29. | {8; 6; 4} | {10; 5; 5} | {5; 6; 8} | {8; 10; 7} |
| 30. | {7; 7; 3} | {6; 5; 8} | {3; 5; 8} | {8; 4; 1} |
Задание № 5
В задачах 1-10 составить уравнение линии, для каждой точки которой ее расстояние до точки A (x 1; y 1) равно расстоянию до прямой y = b. Полученное уравнение привести к простейшему виду и построить кривую.
1. А (2; 1), b = -1. 2. А (– 2; – 2), b = – 4.
3. А (2; – 1), b = 2. 4. А (2; – 1), b = 1.
5. А (4; – 1), b = 1. 6. А (2; 5), b = 1.
7. А (3; – 4), b = 2. 8. А (– 4; 3), b = – 1.
9. А (– 2; – 3), b = – 1. 10. А (1; – 1), b = 3.
В задачах 11-20 даны координаты точек  и
и  . Требуется:
. Требуется:
1) составить каноническое уравнение эллипса, проходящего через данные точки A и B;
2) найти полуоси, фокусы и эксцентриситет этого эллипса;
3) построить эллипс.
11. А  , В
, В  .
.
12. А  , В
, В 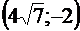 .
.
13. А  , В
, В  .
.
14. А