Бесконечно малые пределы

 

Ф-ция называется бесконечно малой при

Другими словами, если

1. Алгебраическая сумма бесконечно малых функций есть функция бесконечно малая.

Пусть

Из этого следует, что

1. Произведение бесконечно малой функции на ограниченную функцию есть величина бесконечно малая.

Пусть

Следствия.

a) Произведение постоянной величины на бесконечно малую есть ф-ция бесконечно малая.

Пусть функция Тогда существует такое число , что

для всех -окрестности точки х₀. И пусть – бесконечно малая ф-ция, при . Тогда для выполняется неравенство

Следовательно, .

Это означает, что при есть бесконечно малая ф-ция.

b) Произведение двух бесконечно малых есть бесконечно малая функция.

c) Произведение бесконечно малой на число есть функция бесконечно малая.

 

АРИФМЕТИКА ПРЕДЕЛОВ.

1. Предел алгебраической суммы двух ф-ций равен алгебраической сумме их пределов.

Пусть , .

Тогда

– бесконечно малая ф-ция.

Следствие.

Если ф-ция имеет предел, то этот предел единственный.

Доказательство.

Пусть

 

1. Предел произведения двух ф-ций равен произведению пределов этих ф-ций, если пределы сомножителей существуют.

 

Следствие

Постоянную величину можно выносить за знак предела.

 

1. Предел частного двух ф-ций равен частному от пределов этих ф-ций при условии, что пределы делимого и делителя существуют и предел делителя не равен 0.

 

 

ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ.

1 замечательный предел.

Доказательство. Функция – четная на , поэтому рассматриваем на . Из геометрических соображений т.е. на или на . Т.к. то по признаку существования пределов (Если 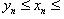и , то ) следует .

2 замечательный предел.

Пусть х→∞. Каждое значение х заключено между двумя положительными целыми числами:

Если x→∞, то n→∞, тогда

По признаку о существовании пределов:

НЕПРЕРЫВНЫЕ ФУНКЦИИ И ИХ СВОЙСТВА.

Пусть функция y=f(x) определена в точке х₀ и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке х₀, если существует предел функции в этой точке и он равен значению функции в этой точке:

Это означает:

- функция определена в точке х₀ и в ее окрестности;

- функция имеет предел при х→х₀

- предел функции в точке х₀ равен значению функции в этой точке, т.е. выполняется равенство.

Это означает, что при нахождении предела непрерывной функции f(x) можно перейти к пределу под знаком функции, то есть в функции f(x) вместо аргумента х подставить предельное значение х₀

1) Сумма, разность и произведение непрерывных в точке х₀ функций – есть функция, непрерывная в точке х₀.

2) Частное двух непрерывных функций – есть непрерывная функция при условии, что g(x) не равна нулю в точке х₀.

3) Суперпозиция непрерывных функций – есть непрерывная функция.

Это свойство может быть записано следующим образом:

Если u = f(x), v = g(x) – непрерывные функции в точке х = х0, то функция v = g(f(x)) – тоже непрерывнаяфункция в этой точке.

4)Функция, непрерывная в точке, является ограниченной в некоторой окрестности этой точки.

Точки разрыва функции – это точки в которых нарушается непрерывность функции.

Точка разрыва х₀ называется точкой разрыва 1 рода функции y=f(x), если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы)

и

При этом, если:

- А1=А2 то точка х₀ называется точкой устранимого разрыва;

- А1≠А2 то точка х₀ называется точкой конечного разрыва.

|A1 – A2| называется скачком функции.

Точка разрыва х₀ называется точкой разрыва 2 рода функции y=f(x), если по крайней мере один из односторонних пределов (слева или справа) не существует, либо равен бесконечности.

ЗАДАЧА О КАСАТЕЛЬНОЙ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ.

Задача о касательной

Касательной к данной кривой в данной точке М называется предельное положение МТ секущей ММ₁, проходящей через точку М, когда вторая точка пересечения М₁ неограниченно приближается по кривой к точке М₁.

Рассмотрим график непрерывной кривой , имеющей в точке М (х;у) невертикальную касательную. Найдем ее угловой коэффициент – угол касательной с осью Ох.

Для этого проведем через точку М и точку М₁ графика с абсциссой секущую. Обозначим через угол между секущей ММ₁ и осью Ох. Видно, что угловой коэффициент равен

При в силу непрерывности функции приращение тоже стремится к нулю; поэтому точка М₁ неограниченно приближается по кривой к точке М, а секущая ММ₁ поворачиваясь около точки М, переходит в касательную. Угол

Следовательно, .

Поэтому угловой коэффициент касательной равен

 

Определение производной

Рассмотрим функцию f(x), область определения которой содержит некоторый открытый интервал вокруг точки x₀. Тогда функция f(x) является дифференцируемой в точке x₀, и ее производная определяется формулой

 

ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.

Рассмотрим движение точки по прямой. Пусть задана координата точки в любой

момент времени x(t). Известно (из курса физики), что средняя скорость за

промежуток времени [t0; t0+ ∆t] равна отношению

расстояния, пройденного за этот промежуток времени, на время, т.е.

Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при

∆t → 0.

lim Vср (t) = n(t0) - мгновенная скорость в момент времени t0

, ∆t → 0.

а lim = ∆x/∆t = x'(t0) (по определению производной).

Итак, n(t) =x'(t).

Физический смысл производной заключается в следующем: произ­водная функции y

= f(x) в точке x0 - это скорость изменения функции f (х) в точке x

Производная применяется в физике для нахождения скорости по известной функции

координаты от времени, ускорения по известной функции скорости от времени.

u(t) = x'(t) - скорость,

a(f) = n'(t) - ускорение, или

a(t) = x"(t).

Если известен закон движения материальной точки по окружности, то можно найти

угловую скорость и угловое ускорение при вращательном движении:

φ = φ(t) - изменение угла от времени,

ω = φ'(t) - угловая скорость,

ε = φ'(t) - угловое ускорение, или ε = φ"(t).

Если известен закон распределения массы неоднородного стержня, то можно найти

линейную плотность неоднородного стержня:

m = m(х) - масса,

x Î [0; l], l - длина стержня,

р = m'(х) - линейная плотность.

С помощью производной решаются задачи из теории упругости и гармонических

колебаний. Так, по закону Гука

F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив

ω2 =k/m, получим дифференциальное уравнение пружинного маятника

х"(t) + ω2x(t) = 0,

где ω = √k/√m частота колебаний (l/c), k - жесткость пружины

(H/m).

Уравнение вида у" + ω2y = 0 называется уравнением гармонических

колебаний (механических, электрических, электромагнитных). Решени­ем таких

уравнений является функция

у = Asin(ωt + φ0) или у = Acos(ωt + φ0), где

А - амплитуда колебаний, ω - циклическая частота,

φ0 - начальная фаза.

ПРОИЗВОДНАЯ В ХИМИИ

Определение скорости химической реакции

Так как скорость реакции v непрерывно изменяется в ходе процесса, ее обычно выражают производной концентрации реагирующих веществ по времени.

Количество в-ва в момент времени t0 c = c(t) - Функция

Интервал времени ∆t = t2 – t1 - Приращение аргумента

Изменение количества в-ва ∆c = c(t+ t) – c(t) - Приращение функции

Средняя скорость химической реакции ∆c/∆t - Отношение приращён. функции к приращён. аргументу

Предел отношения приращённой функции к приращённому аргументу при стремлении Δt к нулю - есть скорость химической реакции в данный момент времени.

выражение v = c/t позволяет определить лишь среднюю скорость реакции за выбранный отрезок времени. Ученых же, как правило, интересует скорость в выбранный момент времени, т.е. так называемая мгновенная скорость реакции. Она определяется как производная функции c(t):

ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ ФУНКЦИЙ

При доказательстве правил дифференцирования будем считать функции f(x) и g(x) дифференцируемыми на некотором промежутке X. То есть, для любого справедливо , где 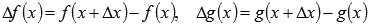- приращения соответствующих функций.

В другой записи

Вынесение постоянного множителя за знак производной. Докажем формулу По определению производной имеем:

Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому

Производная суммы, производная разности. Для доказательства второго правила дифференцирования воспользуемся определением производной и свойством предела непрерывной функции

.

Подобным образом можно доказать, что производная суммы (разности) n функций равна сумме (разности) n производных

Производная произведения функций. Докажем правило дифференцирования произведения двух функций . Запишем предел отношения приращения произведения функций к приращению аргумента. Будем учитывать, что и (приращение функции стремиться к нулю при приращении аргумента, стремящемся к нулю).

Производная частного двух функций (производная дроби). Докажем правило дифференцирования частного двух функций (дроби) Стоит оговориться, что g(x) не обращается в ноль ни при каких x из промежутка X. По определению производной

ПРОИЗВОДНЫЕ ОТ ОСНОВНЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ.

По определению производной для функции синуса имеем

Воспользуемся формулой разности синусов: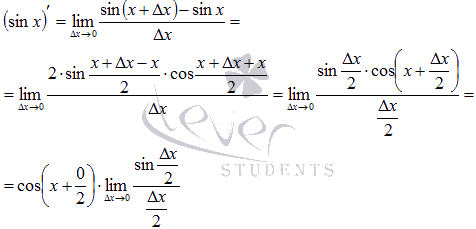

Осталось обратиться к первому замечательному пределу:

Абсолютно аналогично доказывается формула производной косинуса.

ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ.

Сложная функция – это функция, аргументом которой также является функция.

Формула нахождения производной сложной функции.

"Двухслойная" сложная функция записывается в виде

где u = g(x) - внутренняя функция, являющаяся, в свою очередь, аргументом для внешней функции f.

Если f и g - дифференцируемые функции, то сложная функция также дифференцируема по x и ее производная равна

Данная формула показывает, что производная сложной функции равна произведению производной внешней функции на производную от внутренней функции. Важно, однако, что производная внутренней функции вычисляется в точке x, а производная внешней функции - в точке u = g(x)!.

 

Производная обратной функции. Производные обратных тригонометрических функций.

Пусть функции y = f(x) и x = g(y) взаимно обратные, определенные на интервалах и соответственно. Если в точке существует конечная отличная от нуля производная функции f(x), то в точке существует конечная производная обратной функции g(y), причем . В другой записи

Можно это правило переформулировать для любого x из промежутка , тогда получим

 

Для обратной функцией является . Тогда по формуле производной обратной функции получаем

Для арккосинуса все делается абсолютно аналогично:

Найдем производную арктангенса. Для обратной функцией является .

Следовательно,

Схожим образом находится производная арккотангенса:

ПРОИЗВОДНАЯ ЛОГАРИФМИЧЕСКОЙ ФУНКЦИИ.

, по определению производной

 

ПРОИЗВОДНАЯ СТЕПЕННОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ.

, , , ;

y = xⁿ; ln y = n ln x; (ln y)’ = (n ln x)’; ; подставив место y выражение xⁿ получим .

ТЕОРЕМА ЛАГРАНЖА И ЕЁ СЛЕДСТВИЯ.

пусть функция f(x) определена и дифференцируема на промежутке (a;b) и x₁, x₂ – произвольные точки промежутка х₁<x₂, величина f(x₂)-f(x₁) называется конечным приращением функции. Конечное приращение равно произведению приращения аргумента функции на производную, вычисленную в промежуточной между x₁ и x₂ точке. f(b)-f(a)=(b-a)f’(c). Геометрически формула выражает, что на кривой y = f(x) найдётся точка [c, f(c)], касательная в которой параллельна хорде, проходящей через точки [a, f(a)]и [b, f(b)].

найдем f(x1), f(x2). проведем прямую (x1, f(x1))(x2,f(x2)). она пересекает ось Ох под углом α.

tgα=

будем перемещать секущую параллельно самой себе, пока она не станет касательной к графику функции. Она касается графика в точке с абсциссой С

tgα – производная от ф-ции, соответствующей точке

=f^’(c)

F(x₂)-f(x₁)=f^’(c)*(х₂-х₁)

 

Следствия из теоремы Лагранжа

1. Пусть функция f непрерывна на [a,b] и дифференцируема в интервале (a,b). Тогда для того, чтобы функция f на [a,b] была константой необходимо и достаточно, чтобы .

2. дифференцируемые функции производные которых равны для промежутка отличаются самое большее на постоянное слагаемое. f₂(x)-f₁(x)=c

f₁^’(x)=f₂^’(x)

f₁(x)=f₂(x)

f(c)=0

(f₁(x)-f₂(x))^’=f₁^’(x)-f₂^’(x)=c

f₂(x)-f₁(x)=c, f₂(x)=f₁(x)+c

корень уравнения f(x)=0 часто называется нулем функции f(x)

3.Между двумя последовательными нулями дифференцируемой функции лежит по меньшей мере один нуль ее производной

Доказательство

Пусть х₁, х₂ – нули f(x), x₂<x₁

f(x₂)-f(x₁)=(x₂-x₁)*f^’(c), где с (х₁; х₂)

0=(x₂-x₁)*f^’(c)

x₂ x₁ f^’(c)=0

 

МОНОТОННОСТЬ ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ

Возрастающие и убывающие функции также называются монотонными.

Теорема (необходимый признак монотонности функции)

Если дифференцируемая функция возрастает, то ее производная неотрицательна. Ели же дифференцируемая функция убывает, то ее производная неположительна.

Рассмотрим две достаточно близкие точки х и Δх

Найдем

Если f(x) – ф-ция возрастающая, то знак этого отношения совпадает со знаком приращения Δх.

Если f(x) – ф-ция убывающая, то знак отношения противоположен знаку Δх.

Поэтому

·

·

ч.т.д.

Это необходимый признак экстремума.

Теорема (достаточное условие монотонности ф-ции)

Если производная дифференцируемой функции больше 0 на промежутке, то ф-ция возрастает на этом промежутке.

Если производная отрицательна на промежутке, то ф-ция убывает.

Пусть – точки промежутка, на котором ф-ция возрастает. По теореме Лагранжа:

Левая часть этого равенства положительна

называется точкой максимума , если существует окрестность этой точки такая, что для всех из этой окрестности.

Значение в точке – максимум

Аналогично, называется точкой минимума , если существует окрестность этой точки такая, что для всех из этой окрестности.

Значение в точке – минимум

 

ЭКСТРЕМУМЫДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ.

Точка a называется точкой максимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≥ f (x).

Точка a называется точкой минимума функции f, если существует такая ε-окрестность точки a, что для любого x из этой окрестности выполняется неравенство f (a) ≤ f (x).

Точки, в которых достигается максимум или минимум функции, называются точками экстремума. В точке экстремума происходит смена характера монотонности функции. Так, слева от точки экстремума функция может возрастать, а справа – убывать. Согласно определению, точка экстремума должна быть внутренней точкой области определения.

Если для любого (x ≠ a) выполняется неравенство f (x) ≤ f (a) то точка a называется точкой наибольшего значения функции на множестве D:

Если для любого (x ≠ b) выполняется неравенство f (x) > f (b) то точка b называется точкой наименьшего значения функции на множестве D.

Точка наибольшего или наименьшего значения может быть экстремумом функции, но не обязательно им является.

Точку наибольшего (наименьшего) значения непрерывной на отрезке функции следует искать среди экстремумов этой функции и ее значений на концах отрезка.

ПРАВИЛО ЛОПИТАЛЯ

Пусть ф-ции - дифференцируемые и такие, что или .

Тогда

если предел последнего соотношения существует, то функции и непрерывны в точке .

Доказательство

ФОРМУЛА ТЕЙЛОРА ДЛЯ МНОГОЧЛЕНА

Пусть функция есть многочлен степени :

Преобразуем этот многочлен также в многочлен степени относительно разности , где – произвольное число, т.е. представим в виде

Для нахождения коэффициентов , ,…, продифференцируем раз равенство:

…

Подставляя в полученные равенства имеем:

…

Подставляю найденные значения , ,…, в равенство получим разложение многочлена в n -й степени по степеням :

 

 

ФОРМУЛА ТЕЙЛОРА ДЛЯ ФУНКЦИИ

Если ф-ция f(x) определаена в некоторой окрестности точки и имеет в ней производные до -го порядка включительно, то для любого из этой окрестности найдется точка такая, что справедлива формула

Можно записать в виде , где

Называется многочленом Тейлора, а

Называется остаточным членом формулы Тейлора, записанным в форме Лагранжа.

При получаем частный случай формулы Тейлора – формулу Маклорена.

 

ФОРМУЛЫМАКЛОРЕНА

1. Для

 

2. Для

 

 

 

3. Для

 

 

 

ПЕРВООБРАЗНАЯ И ИНТЕГРАЛ

функция F(x) называется первообразной для f(x), если F’(x)=f(x).

Если F(x) первообразная, то все остальные первообразные F(x)+c

Пусть F₁(x) и F₂(x) – первообразные f(x). Тогда F₁’(x)=F₂’(x)=f(x), а согласно следствию из теоремы лагранжа (если две функции имеют одинаковые производные, то они отличаются на постоянную с) значит F₁(x)=F₂(x)+c.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

СВОЙСТВА НЕОПРЕДЕЛЁННОГО ИНТЕГРАЛА.

1.Производная от него равна подынтегральной функции, а дифференциал подынтегральному выражению

2. интеграл от дифференциала функции равен этой функции.

3. Ненулевой постоянный множитель можно выносить из под знака интеграла

Доказательство. пусть F(x) – первообразная f(x), значит .

Возьмем (kF(x)+c)’=kf(x)

4.интеграл от алгебраической суммы нескольких функций равен сумме интегралов от этих функций.

Доказательство. . Пусть F(x) и G(x) – первообразные, тогда производная от выражения F(x)+c₁+G(x)+c₂ равна подынтегральной функции стоящей в левой части равенства.

МЕТОД ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ

Метод интегрирования по частям позволяет свести исходный неопределенный интеграл к более простому виду либо к табличному интегралу. Этот метод наиболее часто применяется, если подынтегральная функция содержит логарифмические, показательные, обратные тригонометрические, тригонометрические функции, а также их комбинации.

Доказательство: По правилу дифференцирования произведения имеем

Эти функции также непрерывны, значит можно взять интеграл от обеих частей равенства:

Операция интегрирования обратна дифференцированию:

После перестановок:

ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ И ЕГО СВОЙСТВА.

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x0 < x1 < x2 < xn = b Тогда говорят, что произведено разбиение R отрезка [a;b] Далее выберем произв. точку , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм при , если он существует независимо от разбиения R и выбора точек ξi, т.е. . Функция f(x) называется интегрируемой на [a;b].

Определённый интеграл численно равен площади фигуры, ограниченной осью абсцисс, прямыми x = a и x = b и графиком функции f(x).

Свойства:

1. То есть, значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Это свойство является следствием определения интеграла.

2. Другими словами, при перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Это свойство определенного интеграла также следует из понятия интеграла.

3. для интегрируемых на отрезке [a; b] функций y = f(x) и y = g(x).

Доказательство. Запишем интегральную сумму функции для данного разбиения отрезка и данного выбора точек :

где и - интегральные суммы функций y = f(x) и y = g(x) для данного разбиения отрезка соответственно.

Переходя к пределу при получим , что по определению интеграла равносильно утверждению доказываемого свойства.

4.

Доказательство

5. Если функция y = f(x) интегрируема на отрезке [a; b] и для любого значения аргумента , то .

 

Это свойство доказывается через определение интеграла Римана: любая интегральная сумма для любого выбора точек разбиения отрезка и точек при будет неотрицательной (не положительной).

5. допустимо интегрирование неравенств.

6. Пусть функция y = f(x) интегрируема на интервале X, причем и , тогда .

 

Это свойство справедливо как для , так и для или .

(свойство аддитивности)

7. теорема о среднем значении

Пусть функция f(x) непрерывна на [a, b], тогда .

Доказательство.

 

 

8. производная от интеграла с переменным верхним пределом.

Если функция y = f(x) непрерывна на отрезке [a; b], то для аргумента интеграл вида