Рис. 1.9
|
.
При равномерном вращении угловую скорость называют также угловой частотой вращения. Она показывает, на какой угол поворачивается радиус-вектор, определяющий положение материальной точки, за единицу времени. Величина 
дает число оборотов в единицу времени и называется частотой вращения. Время, за которое частица совершает полный оборот, называется периодом вращения.
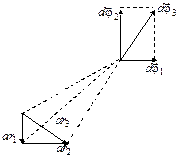Рис. 1.10
|
Вектор угловой скорости можно записать через вектор углового перемещения. Пусть за время 
радиус-вектор, определяющий положение материальной точки, поворачивается на угол 
. Элементарное угловое перемещение характеризуется не только своим значением, но и плоскостью, в которой оно происходит. Чтобы фиксировать эту плоскость следует 
рассматривать как вектор, перпендикулярный этой плоскости. Его направление находится по правилу правого винта: если винт вращать в сторону увеличения 
, то направление движения винта должно совпадать с вектором 
. Однако, чтобы иметь основание определенную так величину называть вектором, необходимо доказать, что она обладает его свойствами.
Действительно, путь, проходимый частицей при очень малом повороте, можно считать прямолинейным. Поэтому два совершаемых последовательно очень малых поворота 
и 
обусловливают, как видно из рис. 1.10, такое же перемещение частицы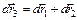 
, как и поворот 
, получаемый из 
и сложением по правилу параллелограмма. Отсюда следует, что очень малые повороты можно рассматривать как векторы. Тогда вектор угловой скорости можно записать следующим образом:
,
а перемещение частицы
. (1.1)
Вектор угловой скорости 
может изменяться как за счет изменения скорости вращения тела, так и за счет поворота оси в пространстве. Пусть за время 
вектор получает приращение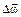 
. Изменение вектора угловой скорости со временем характеризуется величиной
,
которая называется угловым ускорением.
Отдельные точки вращающегося тела имеют различные линейные скорости 
, скорость каждой из точек непрерывно изменяет свое направление. Можно показать, что модуль линейной скорости зависит от угловой скорости и от расстояния до оси вращения. Пусть за малый промежуток времени тело повернулось на угол 
. Точка, находящаяся на расстоянии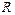 
от оси вращения проходит при этом путь 
. Модуль линейной скорости точки равен
.
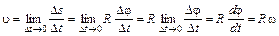Таким образом
. (1.2)
Рис. 1.11
|
Соотношение (1.2) связывает модули линейной и угловой скорости.
Найдем выражение, связывающее векторы и . Положение движущейся точки будем определять радиус-вектором 
, проведенным из начала координат, лежащего на оси вращения. Из рис. 1.11 видно, что векторное произведение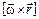 
совпадает по направлению с вектором 
и имеет модуль, равный 
. Следовательно,
.
Последнее выражение можно получить, если поделить (1.1) на .
Нормальное и тангенциальное ускорения материальной точки можно выразить через угловую скорость. Нормальное ускорение можно записать следующим образом:
.
Предположим, что ось вращения не поворачивается в пространстве. Тогда модуль тангенциального ускорения
.
Воспользовавшись соотношением (1.2), тангенциальное ускорение можно представить следующим образом:
,
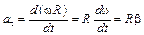где 
– модуль углового ускорения.
Таким образом, нормальное и тангенциальное ускорения растут линейно с увеличением расстояния до оси вращения. Модуль полного ускорения
,
Рис. 1.12
|
а тангенс угла между направлениями нормального и тангенциального ускорений (рис.1.12)
.
Таким образом, направление вектора 
не зависит от 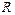, то есть одинаково для всех точек, лежащих на одном радиусе.