Пусть имеются две произвольные системы отсчета S и S', движущиеся относительно друг друга. В системе S заданы скорость 
и ускорение 
некоторой точки. Нужно найти соответствующие значения скорости 
и ускорения 
в системе S'. Рассмотрим последовательно три наиболее важных случая движения одной системы отсчета относительно другой.
1. S' -система движется поступательно по отношению к S -системе.
Рис. 3.1
|
Пусть в S -системе начало отсчета S' -системы характеризуется радиус-вектором 
, а ее скорость и ускорение – векторами 
и 
. Если положение точки А в S -системе определяется радиус-вектором 
, а в S' -системе – радиус-вектором 
, то 
(рис.3.1). Пусть далее за промежуток времени 
точка А совершит в S -системе элементарное перемещение 
. Это перемещение складывается из перемещения 
вместе с S' -системой и перемещения 
относительно S' -системы, то есть 
. Поделив данное выражение на dt, получим следующую формулу преобразования скорости:
. (3.1)
Продифференцировав (3.1) по времени, найдем формулу преобразования ускорения
. (3.2)
Отсюда видно, в частности, что при 
, то есть при движении S' -системы без ускорения относительно S -системы, ускорения точки А в обеих системах отсчета будут одинаковы.
2. S'- система вращается с постоянной угловой скоростью 
вокруг оси, неподвижной в S -системе.
Рис. 3.2
|
Возьмем начало отсчета в S - и в S' -системах в произвольной точке О на оси вращения. Тогда радиус-вектор точки А в обеих системах отсчета будет один и тот же: 
(рис.3.2).
Если точка А неподвижна в S' -системе, то это значит, что ее перемещение в S -системе за время dt обусловлено только поворотом радиус-вектора на угол 
(вместе с S' -системой) и равно, согласно (1.1), векторному произведению 
.
Если же точка А движется относительно S' -системы со скоростью , то за время dt она совершит дополнительное перемещение 
и тогда, как видно из рис. 3.2,
. (3.3)
Поделив это выражение на dt, получим следующую формулу преобразования скорости:
, (3.4)
где и – скорости точки А в S - и S' -системах отсчета соответственно.
Найдем связь между ускорениями в разных системах отсчета. В соответствии с (3.4) приращение 
вектора за время в S -системе должно складываться из суммы приращений векторов и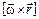 
, то есть
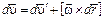. (3.5)
Рис. 3.3
|
Найдем 
. Если точка А движется в S' -системе с постоянной скоростью (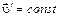
), то приращение этого вектора в S -системе обусловлено только его поворотом на угол (вместе с S' -системой) и равно, как и в случае с 
, векторному произведению 
. В этом не трудно убедиться, совместив начало вектора с осью вращения. Если же точка А имеет ускорение в S' -системе, то за время вектор получит еще дополнительное приращение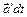 
и тогда
. (3.6)
Подставим (3.3) и (3.6) в равенство (3.5) и полученное выражение разделим на dt. В результате найдем следующую формулу преобразования ускорения:
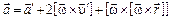, (3.7)
где и – ускорения точки А в S - и S' -системах отсчета. Второе слагаемое в правой части этой формулы носит название кориолисова (или поворотного) ускорения 
, а третье слагаемое – осестремительного ускорения 
:
, 
. (3.8)
Осестремительное ускорение в каждой точке направлено перпендикулярно плоскости, в которой лежат вектора линейной и угловой скоростей вращения неинерциальной системы отсчета.
Таким образом, ускорение точки относительно S- системы равно сумме трех ускорений: ускорения относительно S' -системы, кориолисова ускорения и осестремительного ускорения .
Осестремительное ускорение можно представить в виде 
, где 
– радиус-вектор, перпендикулярный оси вращения и характеризующий положение точки А относительно этой оси. Тогда формулу (3.7) можно записать так:
= 
. (3.9)
3. S' -система вращается с постоянной угловой скоростью 
вокруг оси, перемещающейся поступательно со скоростью и ускорением 
по отношению к S -системе.
Этот случай объединяет два предыдущих. Введем вспомогательную S" -систему отсчета, которая жестко связана с осью вращения S' -системы и перемещается поступательно в S -системе. Пусть и 
скорости точки А в S - и S" -системах отсчета, тогда в соответствии с (3.1) 
. Заменив , согласно (3.4), выражением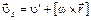 
, где – радиус-вектор точки А относительно произвольной точки на оси вращения S' -системы, получим следующую формулу преобразования скорости:
. (3.10)
Аналогичным образом, используя (3.2) и (3.9), найдем формулу преобразования ускорения:
. (3.11)
Напомним, что в последних двух формулах , и , – скорости и ускорения точки А соответственно в S - и S' -системах отсчета, и – скорость и ускорение оси вращения S' -системы в S -системе, – радиус-вектор точки А относительно произвольной точки на оси вращения 
-системы, – радиус-вектор, перпендикулярный оси вращения и характеризующий положение точки А относительно этой оси.
Силы инерции
Рассмотрим две системы отсчета: инерциальную S -систему и неинерциальную S' -систему. Пусть известны масса частицы m, сила 
, действующая на нее со стороны окружающих тел, и характер движения S' -системы относительно S -системы.
В общем случае S' -система вращается с постоянной угловой скоростью 
вокруг оси, перемещающейся поступательно с ускорением 
относительно S -системы. Согласно (3.11),
. (3.12)
Умножив обе части (3.12) на массу 
частицы и учтя, что в инерциальной системе отсчета 
, получим
. (3.13)
Это и есть основное уравнение динамики в неинерциальной системе отсчета, которая вращается с постоянной угловой скоростью 
вокруг оси, перемещающейся поступательно с ускорением . Из него видно, что даже при 
, частица будет двигаться в этой системе с ускорением, в общем случае отличным от нуля, причем так, как если бы на нее действовали некоторые силы, соответствующие трем членам уравнения (3.13). Эти силы назвали силами инерции. Уравнение (3.13) показывает, что введение сил инерции позволяет сохранить по форме основное уравнение динамики и для неинерциальных систем: слева – произведение массы частицы на ее ускорение (но уже для неинерциальной системы отсчета), справа – силы. Однако кроме силы , обусловленной действием окружающих тел, необходимо учесть и силы инерции – остальные слагаемые в правой части уравнения (3.13).
Перепишем уравнение (3.13) в таком виде:
, (3.14)
где
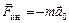(3.15)
– поступательная сила инерции, обусловленная поступательным движением неинерциальной системы отсчета;
(3.16)
– центробежная сила инерции;
(3.17)
– сила Кориолиса, или кориолисова сила инерции. Последние две силы обусловлены вращательным движением системы отсчета.
Мы видим, таким образом, что силы инерции зависят от свойств неинерциальной системы отсчета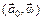 
, а также от радиус-вектора и скорости частицы в этой системе отсчета.
Если, например, неинерциальная система отсчета движется поступательно по отношению к инерциальной системе отсчета, то в этой системе на свободную частицу действует только сила (3.15), направление которой противоположно ускорению данной системы отсчета. Вспомним, как при резком торможении вагона силы инерции бросают нас вперед, то есть в сторону, противоположную вектору .
Силы инерции реально действуют на материальную точку в неинерциальной системе отсчета и могут быть измерены, например, с помощью пружинного маятника. Однако в отличие от обычных ньютоновских сил (сил взаимодействия между телами) для сил инерции нельзя указать, действие каких именно тел на рассматриваемую материальную точку они выражают. Следовательно, к этим силам не применим третий закон Ньютона. Эта особенность сил инерции не является неожиданной, так как величины 
, 
в уравнении (3.14) обусловлены только неинерциальностью системы отсчета и никак не связаны с действием на материальную точку со стороны других тел, учитываемым вектором .
Важно подчеркнуть, что благодаря отмеченной особенности сил инерции, в неинерциальных системах отсчета не существует замкнутых систем тел – для любого из тел системы силы инерции являются внешними. Поэтому в неинерциальных системах отсчета не выполняются законы сохранения импульса, момента импульса и энергии.
Рассмотрим некоторые простейшие примеры неинерциальных систем.
1. Система движется поступательно с ускорением 
. Если отвлечься от сравнительно слабого суточного вращения Земли, то примером такой системы отсчета может служить лифт, ускоренно поднимающийся или опускающийся по вертикали. Пусть к потолку кабины лифта прикреплен пружинный динамометр, к которому подвешено тело массой . Требуется определить силу, действующую на динамометр, а также ускорение, с которым будет двигаться тело, если его освободить. Рассмотрим решения этой задачи, основанные на использовании как скрепленной с лифтом подвижной неинерциальной системы отсчета, так и неподвижной земной системы отсчета, которую с достаточной степенью точности можно считать инерциальной. В инерциальной системе отсчета, связанной с Землей, на тело действуют две противоположно направленные силы – сила тяжести 
и сила упругости пружины динамометра 
. Равнодействующая этих сил сообщает телу ускорение . На основании второго закона Ньютона
.
Согласно третьему закону Ньютона, сила, действующая на динамометр 
. Тогда из последнего уравнения следует
.
Если тело освободить, то есть нарушить его связь с динамометром, то оно будет свободно падать под действием силы тяжести с ускорением
.
В неиненрциальной системе отсчета, связанной с лифтом, тело неподвижно. На тело действуют три силы 
и 
. Поэтому на основании уравнения (3.14)
или
,
откуда для 
получается то же самое значение, что и найденное выше:
.
Если тело освободить, то оно будет двигаться под действием двух сил 
и с ускорением
.
2. Система равномерно вращается с угловой скоростью . Примером такой системы отсчета может служить скамья Жуковского. Поместим на нее небольшой шар. Если скамья Жуковского не вращается, то шар лежит неподвижно. Если скамья вращается, то шар соскальзывает с нее. Рассмотрим объяснение этого опыта в инерциальной и неинерциальной системах отсчета.
В инерциальной системе отсчета на шар действуют две взаимно уравновешивающиеся силы – сила тяжести 
и сила реакции скамьи (влиянием трения шара о гладкий столик можно пренебречь). Начальная скорость шара равна линейной скорости той точки А столика, куда был положен шар. Если расстояние от оси вращения до точки А равно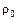 
, угловая скорость вращения , то вектор направлен по касательной к окружности радиуса 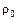и численно равен 
. Так как 
, то шар, положенный на столик, движется по инерции с постоянной скоростью до тех пор, пока не упадет, дойдя до края столика.
В неинерциальной системе отсчета, связанной с вращающейся скамьей, на шар действуют три силы: , и центробежная сила инерции . Первые две силы взаимно уравновешиваются. Поэтому шар движется под действием силы , ускоренно удаляясь от оси вращения.
В процессе движения шара по столику на шар действует также кориолисова сила инерции 
. Эта сила перпендикулярна к скорости шара относительно столика и параллельна горизонтальной плоскости. Поэтому относительно неинерциальной системы отсчета шар движется по криволинейной траектории. Для измерения центробежной силы инерции человек, сидящий на вращающемся стуле, должен удерживать шар с помощью пружинного динамометра так, чтобы шар был неподвижен относительно столика и кориолисова сила инерции равнялась нулю.
Таким образом, любую механическую задачу можно решать как в инерциальной, так и в неинерциальной системах отсчета. Выбор системы отсчета обычно диктуется или постановкой задачи, или стремлением получить решение возможно более простым путем. При это часто удобно пользоваться именно неинерциальными системами отсчета.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ..........................................................................................................
1. КИНЕМАТИКА...............................................................................................
1.1. Пространство и время.........................................................................
1.2. Системы отсчета................................................................................
1.3. Материальная точка.........................................................................
1.4. Способы описания движения материальной точки. Скорость. Ускорение
1.5. Кинематика вращательного движения........................................
1.6. Степени свободы и обобщенные координаты...........................
2. ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ..............................................
2.1. Первый закон Ньютона. Инерциальные системы отсчета.....
2.2. Сила. Масса тела...............................................................................
2.3. Второй закон Ньютона.....................................................................
2.4. Роль начальных условий.................................................................
2.5. Третий закон Ньютона......................................................................
2.6. Принцип относительности Галилея. Преобразования Галилея
3. ДВИЖЕНИЕ В НЕИНЕРЦИАЛЬНЫХ СИСТЕМАХ ОТСЧЕТА.....
3.1. Кинематика относительного движения.......................................
3.2. Силы инерции......................................................................................
Налоговая льгота по К-ОКП ОК-005-93, код продукции 954240
Изд. лиц. ЛР № 064401 от 22.01.96. Подписано к печати 12.01.2001.
Формат 60´84 1/16. Бумага белая писчая. Печать офсетная. Гарнитура "Таймс".
Усл. печ. л. 2,56. Уч.-изд. л. 2,86. Тираж 100 экз.
ЗАО "Издательство научно-технической литературы"
634050, Томск, пр. Ленина, 34а, тел. (382-2) 23-33-35
Копировальный центр "Южный",
Свид. ПД – Г №526,
г.Томск, ул. 19-й Гв. дивизии, 25