Реакция второго порядка имеет вид:
(5)
Будем считать, что исходные концентрации реагирующих веществ (а если речь идет о модели каких-то биологических процессов – исходные численности взаимодействующих элементов системы) равны при 
соответственно 
и 
. Обозначим 
- количество каждого из реагирующих веществ, израсходованного в течение времени 
. Поскольку вещества взаимодействуют в отношении 1:1, для каждого из них будет иметь одно и то же значение. Поэтому кинетическое уравнение можно записать так:
(6)
Это дифференциальное уравнение с разделяющимися переменными. Произведя эту операцию, получим
Используя алгебраическое тождество
получим удобный для интегрирования вид уравнения (6):
После интегрирования и нахождения постоянной интегрирования из условия при 
получим
Или
(7)
Легко убедиться, что при наличии большого избытка одного из реагентов, например, так что по все время процесса можно считать постоянной, реакция будет протекать как реакция первого порядка 
выражение для (что соответствует количеству продукта в правой части (5)) будет иметь вид такой же, как и в предыдущем разделе. Подобная ситуация типична для биохимических процессов, где вода является одним из реагирующих веществ, поскольку в большинстве биологических систем она присутствует в избытке, так что концентрация ее всегда практически постоянна.
Рассмотрим один пример реакции второго порядка. В уравнении реакции первого порядка, описывающем скорость размножения клеток
величина 
не является постоянной, так как следует учитывать, что клетки не только размножаются, но и погибают, выбывая из процесса экспоненциального роста. Поэтому Ферхюльстом и Пирлем (в 1924 г.) была предложена зависимость от числа клеток
так что кинетическое уравнение приняло вид
где 
и 
– константы.
Очевидно, что это уравнение второго порядка. Его решение имеет вид
Линейные цепи реакций
Множество метаболических процессов и процессов более высокого уровня биологической организации представляют цепи последовательных превращений, которые можно упрощенно представить в виде трехзвенной цепи: субстрат - промежуточный продукт – конечный продукт:
(8)
Оговорим вновь условия протекания процесса. При 
и 
. Система закрытая, так что 
в любой момент времени. Запишем систему уравнений:
(9)
Решение первого из уравнений (9) можно записать сразу:
Из условия постоянства массы вещества в системе имеем:
Подставляя это выражение в последнее из уравнении (9), получим
(10)
Общее решение этого уравнения с правой частью, отличной от нуля, как известно, складывается из решения однородного уравнения
и частного решения неоднородного уравнения. Это частное решение будем искать в виде
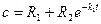
где 
и 
- искомые постоянные. Подставляя это выражение в уравнение (10), получим
Приравнивая свободные члены и коэффициенты при экспонентах, найдем
Полное решение уравнения (10) выглядит с учетом общего решения однородного уравнения так:
Из начальных условий найдем константу интегрирования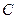 
:
В окончательном виде решение для с запишется:
Выражение для находится без труда из условия сохранения количеств вещества. После несложных преобразовании оно приводится к виду:
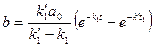
Частным случаем трехзвенной цепи является также последовательность превращений первого и пулевого порядков
В этом случае кинетические уравнения упрощаются:
и дают такие решения (при сохранении указанных условий):
Характерными примерами подобных цепей являются многие ферментативные реакции при высоких концентрациях субстрата, некоторые стадии всасывания аминокислот, условия размножения насекомых и др.