Алгоритм двухэтапного симплекс-метода

Курсовая работа

по дисциплине «Программирование и основы алгоритмизации (Введение в исследование операций)»

 

Выполнила: Пагава Т.

Студентка 1 курса,

Гр. 1о-109с

Проверила: Топорова М.И.

 

Москва 2012г

Содержание

 

1. Условие задачи…………………………………………………………………………….. 3

2.Формализация задачи………………………………...……………………….. 3

3. Методы решения……………………………………………………………… 5

4.Решение задачи………………………………………………………………... 4

Симплекс метод ………………………………………………………….. 8

 

1. Условие задачи

Издательство, показатели деятельности которого отражены в таблице, выпускает литературу четырех серии.

 

Показатель	Серия
Себестоимость единицы продукции, р./экз.   Удельная пропускная способность типографии, оттиск/экз.   Удельный расход бумаги, лист/экз.	0,5

 

Прибыль от реализации ед. продукции (р./экз.) соответственно для каждой серии: 2,3,4,5. Издательство располагает финансовыми средствами в 10000р., лимитами на бумагу в размере 90000 лис. И пропускной способностью типографии, 110000 оттисков. Поступило предписание, что тиражи серий не должны быть менее 2000, 1300, 1500 и 1000 экз. соответственно. При каких тиражах выпускаемых серий издательство получит максимальную прибыль? Как изменится решения задачи, если у издательства появится возможность получить дополнительные финансовые средства? Насколько имеет смысл их увеличить?

2. Формализация задачи.

Требуется найти тиражи выпускаемых серий, при которых прибыль от их реализации максимальна.

В качестве критериальной функции L возьмем прибыль от реализации продукции. Таким образом, мы принимаем в качестве параметров, описывающих работу типографии тиражи соответствующих серий:

 

Х₁ – тираж первой серии при этом X₁≥ 2000

Х₂ – тираж второй серии Х₂≥ 1300 (1)

Х₃ – тираж третий серии Х₃≥1500

Х₄ – тираж четвертой серии Х₄≥1000

 

И

L=2х₁+3Х₂+4х₃+5х₄ (2)

 

Рассмотрим пропускную способность типографии, она равна 110000, мы принимаем в качестве параметров, описывающих количество оттисков на экземпляр при производстве:

 

Первого тиража – Х₁

Второго тиража – 5Х₂

Третьего тиража – 2Х₃

Четвертого тиража – 2Х₄

 

Поэтому:

 

Х₁+5Х₂+3Х₃+2Х₄ ≤ 110000 (3)

 

Рассмотрим ограничения на бюджет. Себестоимость тиража:

 

Первой серии – 0,5Х₁

Второй серии – 4Х₂

Третьей серии – Х₃

Четвертой серии – 4Х₄

 

При этом бюджет ограничен 10000 р.

 

Поэтому:

 

0,5Х₁+2Х₂+Х₃+4Х₄ ≤ 10000 (4)

 

Рассмотрим ограничения на бумагу: расход бумаги на тираж

 

Первой серии – 3Х₁

Второй серии – 4Х₂

Третьей серии – 2Х₃

Четвертой серии – Х₄

 

При этом лимит на бумагу 90000 л.

 

Поэтому

 

3Х₁+4Х₂+2Х₃+Х₄ ≤ 90000 л. (5)

 

Необходимо найти такие значения Х₁, Х₂, Х₃, Х₄, которые удовлетворяют ограничениям (1,3,4,5) и обеспечивают максимум критериальной функции (2)

 

Цель задачи – получение максимальной прибыли – может быть достигнута несколькими способами. Математическим выражением цели является критериальная (целевая) функция L, структура которой отражает вклад каждого из способов в достижении цели. В сформулированной задаче представлено n таких способов. Под способом достижения цели в сформулированной задаче понимается получение прибыли от одного тиража.

Коэффициент С_j представляет собой удельную прибыль при применении j-го способа достижения цели. (В нашем случае прибыль от реализации j-го типа тиража). Отсюда целевая функция также имеет стоимостное выражение.

Переменные X_j – искомые величины, представляющие собой интенсивность использования j-го способа достижения цели.

Для достижения цели имеется: m- виды ресурсов; b_i – возможный объем потребления i-го ресурса. Коэффициент a_ij – это «расход» потребления i-го ресурса (пропускной способности) для производства j-го типа.

 

 

3. Методы решения

Данная задача относится к типу целочисленных.

Математическая модель целочисленной задачи:

Максимизировать

L=2Х₁+3Х₂+4Х₃+5Х₄

 

При ограничениях:

 

(1) 0,5Х₁+2Х₂+Х₃+4Х₄ ≤ 10000

3Х₁+4Х₂+2Х₃+Х₄ ≤ 90000

Х₁₁+5Х₂+3Х₃+2Х₄ ≤ 110000

Х₁ ≥ 2000

Х₂≥1300

Х₃≥1500

Х₄≥1000

 

Х_J ≥ 0. Целые j= 1,4

 

 

Экстремальная задача, переменные которой принимают лишь целочисленные значения, называется задачей целочисленного программирования, при их решении используются:

- методы отсечений

- методы разветвлений

- приближенные методы (даны допустимые решения, хотя и в общем случае неоптимальные)

- симплекс метод

-графический метод

- Двухэтапный симплекс (метод применяется к задачам, заданным не в канонической форме.)

 

Сформулированная ранее задача относится к классу задач целочисленного линейного программирования. Небольшая размерность задачи и то, что она не задана в канонической форме, позволяет нам применить двухэтапный симплекс метод.

 

4. Решение задачи

Прежде чем приступить к решению задачи запишем ее в общем виде:

 

(2) 0,5Х₁+2Х₂+Х₃+4Х₄+Х₅ = 10000, Максимализировать

3Х₁+4Х₂+2Х₃+Х₄+Х₆ = 90000,

Х₁₁+5Х₂+3Х₃+2Х₄+Х₇=110000, L= 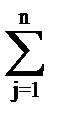С_jX_j

Х₁ -Х₈=2000, при ограничениях

Х₂-Х₉=1300,

Х₃-Х₁₀=1500, 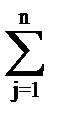a_ij*X_j=b_i

Х₄-Х₁₁=1000,

 

Где Xj≥0; j=1,…,11

 

Алгоритм двухэтапного симплекс-метода

1.

Привести задачу к стандартному виду. Если он является каноническим – решать одноэтапным симплекс-методом (см. 5)

2.

Составить вспомогательную задачу. Решить ее симплекс-методом.

3.

Если вспомогательная задача не имеет решения или по окончании решения получены ненулевые (положительные) коэффициенты в целевой функции вспомогательной задачи, то исходная задача не имеет решения, иначе см.4.

4.

Отбросить вспомогательную целевую функцию, выписать начальное допустимое базисное решение.

5.

Решить полученную каноническую задачу одноэтапным симплекс-методом.

(1.

Составление первого опорного плана. Переход к канонической форме задачи линейного программирования путем введения неотрицательных дополнительных базисных переменных.(метод искусственного базиса).

2.

Проверка плана на оптимальность. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.

3.

Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбирается наибольший по абсолютной величине. Затем элементы столбца свободных членов симплексной таблицы делят на элементы того же знака ведущего столбца.

4.

Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана—Гаусса.)

 

Воспользуемся искусственными переменными, решим следующую задачу (3).

 

(В качестве базиса мы можем взять только переменные Х_5, Х₆, Х₇, нам не хватает еще четырех базисных переменных.)

 

 

L=2Х₁+3Х₂+4Х₃+5Х₄ max

 

0,5Х₁+2Х₂+Х₃+4Х₄+Х₅ = 10000,

3Х₁+4Х₂+2Х₃+Х₄+Х₆ = 90000,

Х₁₁+5Х₂+3Х₃+2Х₄+Х₇=110000,

(3) Х₁ -Х₈+Х₁₂=2000

Х₂-Х₉+Х₁₃=1300

Х₃-Х₁₀+Х₁₄=1500

Х₄-Х₁₁+Х₁₅=1000

Х_12, Х_13, Х_14, Х₁₅ ≥0

Х_1, Х_2, Х_3, Х_4, Х_5, Х_6, Х_7, Х_8, Х_9, Х_10, Х₁₁ ≥0

 

Если эта задача достигает оптимума при нулевых значения искусственных переменных (Х₁₂ - Х₁₅), тогда исходная задача (2) имеет решение и оно совпадает с решением (3).

Воспользуемся двухэтапным методом.

На первом этапе будем минимизировать сумму искусственных переменных (если в результате мы получим ноль, значит задача (2) имеет решение, при этом мы найдем начальный опорный план и сможем перейти ко второму этапу. Что бы минимизировать сумму мы максимизируем W=-(-Х₁₂+Х₁₃+Х₁₄+Х₁₅).

 

Применим двухэтапный симплекс метод.

Исходными данными в подпрограмме является:

1) Размерность матрицы A=min

m=7, n=15

 

2) 0,5 2 1 4 1 0 0 0 0 0 0 0 0 0 0

3 4 2 1 0 1 0 0 0 0 0 0 0 0 0

1 5 3 2 0 0 1 0 0 0 0 0 0 0 0

A= 1 0 0 0 0 0 0 -1 0 0 0 0 0 0 0

0 1 0 0 0 0 0 0 -1 0 0 0 0 0 0

0 0 1 0 0 0 0 0 0 -1 0 0 0 0 0

0 0 0 1 0 0 0 0 0 0 -1 0 0 0 0

 

3) Вектор свободных членов в уравнении ограничений b_i, i=1…m

 

=10000, 90000, 110000, 2000, 1300, 1500, 1000, 0, -5800

 

4) Коэффициент при переменных в критериальной функции С_j

 

J= 1 … n

= (2,3,4,5,0,0,0,0,0,0,0,0,0,0,0)