9. Степенная функция
Ф-я заданная формулой f(x)=xa называется степенной с показателем а.
Цели:
1)обобщить и системат-ть знания уч-ся о степ.ф-и,а также познак-ть с многообразием св-в и гр-ков степ.ф-и в завис-ти от знач-я оснований и показателей степени.
2)Научить решать простейш.иррац.ур-я и неравенства.
Учащиеся должны знать:
-Df и св-ва степенной функции
-Ф-лу произ-й степенной функции (xn)'=nxn-1
Учащиеся должны уметь:
-Применять св-ва степ.ф-и д/исслед-я ф-й и построения графиков
Уч-ся должны представлять себе эскиз гр-ка степ.ф-и у=ха для любого рац.показателя а:
1)Гр-к люб.степ.ф-и проходит ч/з точку (1;1)
2)аÎN, а-чет.-график похож на параболу
3)аÎN,а-нечет,а>1- на кубическую параболу
4)аÎZ, а-нечет, а<0 – на гиперболу
5)аÎZ, а-чет, а<0 – две ветви гиперболы, симметричные относительно Оу
6)аÎQ, a<0 – одна ветвь гиперболы
7)аÎQ,a>0–одна ветвь параболы, ориен-тированная вверх (а>1) и вправо (0<a<1)
Методические замечания
1.Введению степ.ф-и должно предшест-ть повторение уч-ся примеров степ.ф-и
2.изучение св-в степ.ф-и д.б.построено в соот-вии с общ.схемой исслед-я ф-й в зависимости от значений параметра а
3.сделать акцент на изучение этой темы:
в основной школе - аÎN,Z,Q
в старшей школе-аÎR(люб.действит.число)
4.сформировать у уч-ся умение применять общ.пр-ла работы с показателями: aaab=aa+b;(aa)b=aab
Набор заданий и упражнений:
1.Задачи на отработку свойств степеней
2.з-чи на тождеств.преобраз-ния степеней
3.з-чи,форм-щие графич.культуру учащихся
4.реш-е иррац.уравнений и неравенств
5.применение произв-й к степ.ф-и (найти произ-ю,найти знач-е произ-й в точке; Ур-е кас-ной;нах-ние максимума и минимума; вы-числ-е интегралов,площадей плоск. фигур)
Иррациональные уравнения
1)возведение в степень, если уравнение содержит один корень (радикал)
2)если ур-е содержит неск.радикалов, то применяются м-ды: замена пер-й; умн-е на сопряж.множ-ль; преобраз-е иррац.ур-я в систему рациональных уравнений.
Замечание: требуется постоянная проверка равносильности переходов от одного преобразования к другому
Иррациональные неравенства
1) √f(x)<g(x) 2) √f(x)>Ög(x) f(x)<(g(x))2 f(x)>=0
f(x)>=0 g(x)>=0
g(x)>0 f(x)>g(x)
3) √f(x)>g(x) 4) √f(x)<Ög(x)
f(x)>=0 f(x)>=0
g(x)<0 или g(x)>=0
f(x)>=0 f(x)<g(x)
g(x)>=0
f(x)>(g(x))2
10. Показательная ф-я
Сущ-ют 2 подхода к изуч-ю этой темы:
1 подход (Колм., Мордк.):Показ.ф-я изуч-ся в 11 кл позже темы «Произ-я» 10 кл.
«+»:можно опираться на пон-е произ-й при изуч-и св-в ф-и; «-»:таблица произ-х будет сначала неполнойÞу уч-ся не будет сформировано целост.пон-е произ-й элем.ф-и
2 подход (Никольский,Алимов):Показ.ф-ю (10 кл) изучают раньше произ-й (11 кл).
Редко встреч-ся подход,когда внутри самой темы меняются местами изуч-е показ.и лог. ф-и:лог.ф-я рассм.раньше показат.,а показат.ф-я вводится как обратная к лог-кой.
Осн.пон-я:1)степень с иррац.пок-лем; иррац.ур-я; 2)показ.ф-я,ее св-ва и гр-к; 3)тожд.преобр-я показ.выр-й; 4)реш-е показ. ур-й и нер-в с опорой на св-ва показ.ф-и; 5)произ-я показ. ф-и (ax)’=axlna; (ex)’= ex.
Цели: 1)Познакомить уч-ся с показ.ф-ей. 2)Обучить приемам реш-я показ.ур-й и нер-в.
Методич.замечания:
(1)Пон-е корня n степени и степени с рац.по-казателем явл.обобщением пон-й(ранее изученных) кв.корня и степени с цел.пок-лем.
(2)Необ-мо уделить вним-е отработке св-в степеней и фор-ю навыков тожд.преобр-й.
(3)Пон-е степени с иррац.пок-лем вводится на наглядно-интуитивной основе.
(4)Изуч-е св-в показ.ф-и д.б.построено в соотв.с общ.схемой исслед-я.
(5)Вывод ф-лы произ.показ.ф-и производится на нагл.-интуит.основе.
Рассм.дифф.ур-е роста(убывания)пок-ля, сле-дует отметить,что показ.ф-я выступает как матем.модель,используемая для описания реальных процессов.
| a>1
| 0<a<1
| | 1)D(y)=(-µ;+µ)
2)E(y)=(0;+µ)
3)Общ.вида,непериод.
4) на (-µ;+µ)
5)ограничена снизу 0, сверху не огранич
6)не имеет ни наиб., ни наим.знач-й
7)непрерывна
8)выпукла вверх ø
9)Ох-горизонт.ас-та при х®+µ
10)Произ.всегда >0
(2x)’=2xln2>0
| 1)D(y)=(-µ;+µ)
2)E(y)=(0;+µ)
3)Общ.вида,непериод.
4)¯ на (-µ;+µ)
5) ограничена снизу 0, сверху не огранич
6)не имеет ни наиб., ни наим.знач-й
7)непрерывна
8)выпукла вниз è
9)Ох-горизонт.ас-та при х®-µ
10)Произ.всегда <0
((1/2)x)’=(1/2)xln(1/2)<0
| Набор з-ч и упр-й: 1)Чтение гр-ка (по гр-ку описать св-ва). 2)Построение гр-ка показ.ф-и. 3)Тожд.преобр-я показ.выр-й. 4)Исслед.показ. ф-и с пом.произ-й. 5)Реш-е простейш.показ. ур-й и нер-в. 6)С-мы показ.ур-й и нер-в. 7)З-чи на отработку осн.приемов реш-я показ.ур-й и нер-в.
| 11. Логарифмическая ф-я
Сущ-ют 2 подхода к изуч-ю этой темы:
1 подход (Колм., Мордк.):Лог.ф-я изуч-ся в 11 кл позже темы «Произ-я» 10 кл.
«+»:можно опираться на пон-е произ-й при изуч-и св-в ф-и; «-»:таблица произ-х будет сначала неполнойÞу уч-ся не будет сформировано целост.пон-е произ-й элем.ф-и
2 подход (Никольский,Алимов):Лог.ф-ю (10 кл) изучают раньше произ-й (11 кл).
Редко встреч-ся подход,когда лог.ф-я рассм.раньше показат.,а показат.ф-я вводится как обратная к лог-кой.
Осн.пон-я:1)лог.числа,св-ва лог-мов; 2)лог. ф-я,ее св-ва и гр-к; 3)тожд.преобр-я лог.выр-й; реш-е лог.ур-й и нер-в с опорой на св-ва лог. ф-и; 4)пон-е нат.лог-ма,число е; 5)произ-я лог. ф-и (logax)’=1/(xlna); (lnx)’=1/x.
Цели: 1)Познакомить уч-ся с лог.ф-ей. 2)Обучить приемам реш-я лог.ур-й и нер-в.
Методич.замечания:
(1)При изуч-и лог.ф-и нужно обратить вним-е на пон-е взаимнообрат.ф-й на примере показ.и лог.ф-й с одинак.осн-ми. Св-ва лог.ф-и следуют из св-в показ.ф-и и Th об обрат.ф-и. Полезно чтобы уч-ся повторили эту Th.
Th Гр-ки взаимнообрат.ф-й f(x) и g(x) сим-ны отн-но у=х.
Эта Th дает возм-ть легко построить гр-к y=logax, т.к. уже известно,как выглядит гр-к ф-и y=ax.
Пр  (2)Уч-ся должны усвоить обл-ти опр-я и обл-ти знач-я.
(3)Особ.вним.следует уделить осн.лог.тож-ву: alogab=b (b>0,a>0,a≠1),т.к.это св-во исп-ся при реш-и ур-й и нер-в.
(2)Уч-ся должны усвоить обл-ти опр-я и обл-ти знач-я.
(3)Особ.вним.следует уделить осн.лог.тож-ву: alogab=b (b>0,a>0,a≠1),т.к.это св-во исп-ся при реш-и ур-й и нер-в.
| a>1
| 0<a<1
| | 1)D(y)=(0;+µ)
2)E(y)=(-µ;+µ)
3)Общ.вида,непериод.
4) на (0;+µ)
5)не ограничена ни сверху,ни снизу
6)не имеет ни наиб., ни наим.знач-й
7)непрерывна
8)выпукла вверх æ
| 1)D(y)=(0;+µ)
2)E(y)=(-µ;+µ)
3)Общ.вида,непериод.
4)¯ на (0;+µ)
5)не ограничена ни сверху,ни снизу
6)не имеет ни наиб., ни наим.знач-й
7)непрерывна
8)выпукла вниз è
| Набор з-ч и упр-й: 1)Чтение гр-ка (по гр-ку описать св-ва). 2)Построение гр-ка лог.ф-и. 3)Тожд.преобр-я лог.выр-й. 4)Исслед.ф-и с пом.произ-й. 5)Реш-е прост.лог.ур-й и нер-в. 6)З-чи на закрепление осн.лог.тож-ва alogab=b. 7)З-чи на закрепление ф-лы перехода к нов.осн-ю logab=logcb/logca. 8)З-чи на исполь-зование св-в показ.и лог.ф-й:
Пр log2(4+2x)+log2(1-2x)=7
log2((4+2x)(1-2x))=log227
(4+2x)(1-2x)=128…
9)З-чи на отработку осн.приемов реш-я лог. ур-й и нер-в.
Производная функции
$2 подхода к ведению осн.оп-ций мат. анализа (дифф. и интегр.).
1 подход (Колм.,Башм.,Мордк.): «Произ-я»-10кл,«Интеграл»-11 кл.Тема «Произ-я» включает 2 раздела: 1)Пон-е «произ.» и пр-ла дифф. 2)Прилож-я произ-й.
Таблица произ-х неполная, т.к. еще не все элем.ф-и изучены.
2 подход (Алимов,Никольский):Произ-я и инте-гралы изуч-ся др.за др.в 11 кл. с опорой на сформирован.пон-е класса элем.ф-й.Это осн. мат-л 1-го полугодия в 11 кл.
При этом подходе уч-ся логически подводятся к построению таблицы произ-х осн.элем.ф-й.
Цели: 1)Сист-ция знаний об изуч.ранее ф-ях. 2)Познакомить уч-ся с нов. м-дом исслед-я свойств ф-й. 3)Показать применение нов.м-да к реш-ю прикладн.з-ч. 4)Раскрыть роль дифф. для науки. 5)Форм-е науч.стиля мышления у уч-ся.
З-чи,приводящ. к пон-ю произ-й: 1)З-ча о мгновен.ск-ти (мех.смысл). 2)З-ча о кас-й к кривой (геом.смысл).
Актуализация: знаний: 1)ф-я числ.арг-та; 2)∆х, ∆у; 3)ск-ть неравномерн.движ-я,сред.и мгновен.ск-ть; умений: 1)находить знач-е ф-и в точке; 2)находить ∆у по заданному ∆х; 3)на-ходить сред.ск-ть неравномерн.движ-я.
Знания,кот. приобретают уч-ся:
(1)Пон-е произ-й,точки max и min.
(2)Алгоритм нах-ния произв.по опр-ю: а)фиксируем зн-е х;находим f(x); б)даем х приращение ∆х; f(x+∆х); в)нахо-дим ∆f=f(x+∆х)-f(x); г)составляем отн-е: ∆f/∆х; д)находим предел lim∆f/∆х при ∆х→0.
Примеч-е. Применяется пон-е «предельный переход»,т.к.уч-ся не изучают строго орп-е предела ф-и.
(3) Геом.смысл произ-й: y=f(a)+f’(a)(x-a)–ур-е кас-й в точке а.
(4) Физ.смысл произ-й:S(t),t0Þv(t)=S’(t),v(t0)=…
(5)Общ.схему исслед-я ф-и с пом. произ-й.
(6)Достаточ.усл-е монот-ти ф-и (f’(x)³0 ; f’(x)£0 ¯)
(7) Пр-ла дифф.: а) (u+v)’=u’+v’; б) (uv)’=u’v+uv’
в) (u/v)’=(u’v-v’u)/v2;
г) f’(x)=h’(g(x))g’(x) – сложная ф-я.
Пр y’=(cos23x)’=2 cos3x(-sin3x)3=-3sin6x
(8) Таблицу производных: 1)С’=0; 2)(kx+b)’=k 3)(xn)’=nxn-1; 4)(sinx)’=cosx; 5)(cosx)’=-sinx; 6)(tgx)’=1/cos2x; 7)(ctgx)’=-1/sin2x; 8)(ax)’=axlna; 9)(ex)’=ex; 10)(lnx)’=1/x; 11)(logax)’=1/(xlna)
Умения, кот.форм-ся у уч-ся:
(1)Нах-ть произ-ю в точке и на отрезке
(2)Применять произ.для исслед.ф-й:монотон-ность,наличие экстремумов,max и min на отрезке.
(3)Применять произ.для реш-я сюжет.з-ч (физ. и математических).
(4)Применять произ.для приближ.вычислений f(x+∆х)»f(x)+f’(x)∆х
Пр 
f(x)= 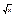 ; x=1; f(x)=1; f’(x)=1/(2 ; x=1; f(x)=1; f’(x)=1/(2 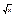 ); f’(1)=1/2; ); f’(1)=1/2;  »1+∆х/2. »1+∆х/2.
| Сложная функция
1. Понятие сложной функции
Рассм. фун-ю y=f(x). Аргументом м.б. какое-либо выр-е, например,
 Пр.
Пр.  Найти Найти 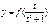
 Пусть f и g – 2 фун-и (y=f(x), x=g(t)).
Подставив вместо х в фун-ю y x=g(t), получим новую фун-ю, в которой аргументом будет t: y=f(g(t)). Эта фун-я наз-ся сложной фун-й или композицией ф-й f и g.
Обозначение: f
Пусть f и g – 2 фун-и (y=f(x), x=g(t)).
Подставив вместо х в фун-ю y x=g(t), получим новую фун-ю, в которой аргументом будет t: y=f(g(t)). Эта фун-я наз-ся сложной фун-й или композицией ф-й f и g.
Обозначение: f  g=f(g(t)).
2. Св-ва композиции фун-й
Пр. y1=x2, y2= g=f(g(t)).
2. Св-ва композиции фун-й
Пр. y1=x2, y2= 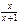 , y1 , y1  y2 -?; y2 y2 -?; y2  y1-?
y1 y1-?
y1  y2= y2=  ; y2 ; y2  y1= y1=  y1 y1  y2 ≠ y2 y2 ≠ y2  y1.
1 св-во: операция композиции фун-ий не коммутативна
Если t y1.
1 св-во: операция композиции фун-ий не коммутативна
Если t  D(g),то фун-я y=f(g(t)) не определена, т.к. чтобы вычислить y, надо найти g(t).
2 св-во: D(y) D(g),то фун-я y=f(g(t)) не определена, т.к. чтобы вычислить y, надо найти g(t).
2 св-во: D(y)  D(g), g- внутр. фун-я
Пр. f(x)= D(g), g- внутр. фун-я
Пр. f(x)=  g(t)=t2+1
D(g)=R
y=f(g(t))= g(t)=t2+1
D(g)=R
y=f(g(t))=  D(y)=(-µ;1)
D(y)=(-µ;1)  (-1;1) (-1;1)  (1; +µ) (1; +µ)  D(g).
3. Производная сложной функции
1. По определению y= D(g).
3. Производная сложной функции
1. По определению y= 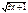 ∆x≠0, х+∆x
∆x≠0, х+∆x  D(y)
y(х+∆x)= D(y)
y(х+∆x)=  ∆y=
∆y=  - -  lim(∆x→0) ∆y/∆x=3/2*√3х+1
lim(∆x→0) ∆y/∆x=3/2*√3х+1
  2. Заполняем таблицу
2. Заполняем таблицу
| y(x)
| f(u)
| f| (u)
| 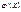
| y|(x)
| | (x+1)2
| u2
| 2u
|
| 2(x+1)
| | sin2x
| sinu
| cosu
|
| 2cos2x
| 
| √u
| 1/2√u
|
| 
| 3. Алгоритм
1) u=g(x)
2) f| (u), g|(x)
3)y|=f|(u)*g|(x) 
Оценка учебников
1. место темы в шк. курсе
2. введение понятия слож. фун-и
Башмаков
1)Понятие вводится в заключ. беседе главы «Фун-я и графики». Автор считает, что изучение этого понятия не обязательно.
2)Сразу вводится определение и обознач., рассм. пример; даётся алгоритм составления слож. ф-и в зависимости от порядка ф-й; рассм. св-ва операции композиции ф-й.
Колмогоров
1) Понятие вводится в главе «Произв. и её применение» в пункте «произв. слож. ф-и»
2) Понятие вводится посредством примера; опред. и обознач.; алгоритм вычисления слож. ф-и в точке; рассм. вопрос об обл. определения сл. ф-и.
Виленкин (углуб)
1) В главе «Фун-и и последов» вводится понятие сл. ф-и и термин композиции фун-ий, как операция над фун=й.
2) Рассм. примеры, опред. и обознач., алгоритм составления композиции фун-й f и g.
Алимов
1) Тема не рассм и понятие сл. ф. не формируется. Но упр-я, связанные со слож. фун-ей, разбросаны по всему учебнику.
2) Специального параграфа нет.
Муравин
1) Понятие ввод. в главе «Техника дифф» в параграфе «Слож.ф-я». Даётся формула дифф. слож. фун-и. Материал обязательный
2)Понятие ввод. на примере, в кот. док-ся возрастание слож. ф-и в силу возраст-я элем. фун-й, входящих в её состав. Определения и обознач. нет. Область опред-я и св-ва слож фун-и не рассм.
Дорофеев
1) Понятие ввод. в главе «Фун-я и графики», но параграфа нет. Ввод. посредством примера, в кот. сл. ф-я непрерывна в силу непрерывности элем. фун-й, входящих в её состав.
2)Даётся Th о непрерывности слож. фун-и; y=f(g(x)), где f- внешняя, g- внутр. Приводится пример.
|
Поиск по сайту:
|
 - период
- период

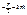

 симметрия относит. (0;0); периодич. на всей числовой оси.
симметрия относит. (0;0); периодич. на всей числовой оси.
 y=cosx
Св-ва фун-и y=cosx аналогично рассматрив-ся. Поэтому целесообразно ввести фун-ю y=cosx с использованием формул приведения
cosx=sinx(x+
y=cosx
Св-ва фун-и y=cosx аналогично рассматрив-ся. Поэтому целесообразно ввести фун-ю y=cosx с использованием формул приведения
cosx=sinx(x+  /2)
Эти фун-и имеют одинаковые по форме графики в силу параллельного переноса графика фун-и y=sinx на вектор (-
/2)
Эти фун-и имеют одинаковые по форме графики в силу параллельного переноса графика фун-и y=sinx на вектор (-  Замечание: св-ва фун-и y=cosx учащиеся могут сформулировать самостоят., опираясь на св-ва sinx и построенного графика.
1. D(f)=(-∞:+∞)=R
2. чёт, cos(-x)=cosx → график симм. относ Oy
3. периодич., Т=2
Замечание: св-ва фун-и y=cosx учащиеся могут сформулировать самостоят., опираясь на св-ва sinx и построенного графика.
1. D(f)=(-∞:+∞)=R
2. чёт, cos(-x)=cosx → график симм. относ Oy
3. периодич., Т=2  y↓ на
y↓ на 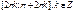 5. огранич. сверху и снизу: -1≤cosx≤1
6. yнаим=-1 для t=
5. огранич. сверху и снизу: -1≤cosx≤1
6. yнаим=-1 для t= 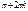 yнаиб=1 для t=
yнаиб=1 для t=  7. непрерывна на R
8. E(f)=[-1;1].
y=tgx
1. D(f)=R, кроме x=
7. непрерывна на R
8. E(f)=[-1;1].
y=tgx
1. D(f)=R, кроме x=  Показываем уч-ся систему координат, на которой пунктиром отмечены прямые. Графиком будет множ-во ветвей м/у пунктир. линиями.
2. периодич., Т=
Показываем уч-ся систему координат, на которой пунктиром отмечены прямые. Графиком будет множ-во ветвей м/у пунктир. линиями.
2. периодич., Т=  - период
tg(x-
- период
tg(x-  до
до  , затем будем сдвигать по Ox вправо и влево на
, затем будем сдвигать по Ox вправо и влево на  5. не огранич. ни снизу, ни сверху.
6. не имеет ни наим., ни наиб. зн-я
7. непрерывна на
5. не огранич. ни снизу, ни сверху.
6. не имеет ни наим., ни наиб. зн-я
7. непрерывна на  , фун-я терпит разрыв→эти прямые будут вертикальными асимптотами.
8. E(f)= (-∞:+∞).
9. График:
, фун-я терпит разрыв→эти прямые будут вертикальными асимптотами.
8. E(f)= (-∞:+∞).
9. График:
 y=ctgx
Уч-ся предлагается самостоятельно построить график ф-и y=-tg(x+
y=ctgx
Уч-ся предлагается самостоятельно построить график ф-и y=-tg(x+  После этого обосновывается, что построили график фун-и y=ctgx, т.к. ctgx=-tg(x+
После этого обосновывается, что построили график фун-и y=ctgx, т.к. ctgx=-tg(x+  /2).
Уч-ся сами могут описать св-ва y=ctgx, опираясь на св-ва tgx и построенный график.
1. D(y)=R, кроме x=
/2).
Уч-ся сами могут описать св-ва y=ctgx, опираясь на св-ва tgx и построенный график.
1. D(y)=R, кроме x=  5. не огранич. ни св., ни снизу
6. не имеет ни мин, ни максим. значения
7. непрерывна на
5. не огранич. ни св., ни снизу
6. не имеет ни мин, ни максим. значения
7. непрерывна на  (2)Уч-ся должны усвоить обл-ти опр-я и обл-ти знач-я.
(3)Особ.вним.следует уделить осн.лог.тож-ву: alogab=b (b>0,a>0,a≠1),т.к.это св-во исп-ся при реш-и ур-й и нер-в.
(2)Уч-ся должны усвоить обл-ти опр-я и обл-ти знач-я.
(3)Особ.вним.следует уделить осн.лог.тож-ву: alogab=b (b>0,a>0,a≠1),т.к.это св-во исп-ся при реш-и ур-й и нер-в.

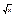 ; x=1; f(x)=1; f’(x)=1/(2
; x=1; f(x)=1; f’(x)=1/(2  Пр.
Пр.  Найти
Найти 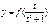
 Пусть f и g – 2 фун-и (y=f(x), x=g(t)).
Подставив вместо х в фун-ю y x=g(t), получим новую фун-ю, в которой аргументом будет t: y=f(g(t)). Эта фун-я наз-ся сложной фун-й или композицией ф-й f и g.
Обозначение: f
Пусть f и g – 2 фун-и (y=f(x), x=g(t)).
Подставив вместо х в фун-ю y x=g(t), получим новую фун-ю, в которой аргументом будет t: y=f(g(t)). Эта фун-я наз-ся сложной фун-й или композицией ф-й f и g.
Обозначение: f  g=f(g(t)).
2. Св-ва композиции фун-й
Пр. y1=x2, y2=
g=f(g(t)).
2. Св-ва композиции фун-й
Пр. y1=x2, y2= 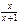 , y1
, y1  ; y2
; y2  y1
y1  D(g),то фун-я y=f(g(t)) не определена, т.к. чтобы вычислить y, надо найти g(t).
2 св-во: D(y)
D(g),то фун-я y=f(g(t)) не определена, т.к. чтобы вычислить y, надо найти g(t).
2 св-во: D(y)  D(g), g- внутр. фун-я
Пр. f(x)=
D(g), g- внутр. фун-я
Пр. f(x)=  g(t)=t2+1
D(g)=R
y=f(g(t))=
g(t)=t2+1
D(g)=R
y=f(g(t))=  D(y)=(-µ;1)
D(y)=(-µ;1)  (-1;1)
(-1;1) 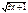 ∆x≠0, х+∆x
∆x≠0, х+∆x  D(y)
y(х+∆x)=
D(y)
y(х+∆x)=  ∆y=
∆y=  -
-  lim(∆x→0) ∆y/∆x=3/2*√3х+1
lim(∆x→0) ∆y/∆x=3/2*√3х+1

 2. Заполняем таблицу
2. Заполняем таблицу