1. Методика изучения многоугольников. Геометрия треугольника. Различные виды четырехугольников
Понятие треугольника вводится в 7 классе и используется на протяжении всего курса геометрии.
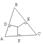
Треугольник – фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.
А, В, С – вершины; АВ, ВС, АС – стороны.
Обозначение: DАВС
Угол DАВС при вершине А – угол, образованный полупрямыми АВ и АС.
Высота – перпендикуляр, проведенный из данной вершины к прямой, содержащей противоположные стороны.
Биссектриса – отрезок биссектрисы угла треугольника, соединяющий данную вершину с точкой на противоположной стороне.
Медиана – отрезок, соединяющий данную вершину с серединой противоположной стороны.
Неравенство треугольника: каковы бы ни были три точки, расстояние между любыми двумя точками не больше суммы расстояний от них до третьей точки.
а£b+c; c£a+b; b£a+c
Равные отрезки – если имеют одинаковую длину.
Два угла называются равными, если они имеют одинаковую угловую меру.
DАВС =DА1В1С1 : АВ= А1В1, … и ÐА=Ð А1, …
Треугольники равны, если у них соответствующие стороны и углы равны.
Признаки равенства треугольников
1. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие равны.
2. Если сторона и прилежащие к ней углы одного треугольника равны стороне и прилежащим к ней углам другого треугольника…
3. Если три стороны одного треугольника равны трем сторонам другого треугольника…
Основные идеи доказательства признаков: (1) и (2) признаки – наложение одного треугольника на другой и доказательство их совмещения. (3) признак – свойства углов равнобедренного треугольника при соответствующих равных сторонах.
Равнобедренный треугольник:
Треугольник называется равнобедренным, если у него две стороны равны. Эти стороны – боковые, а третья – основание.
При изучении свойств и признаков равнобедренного треугольника целесообразно использовать прямую и обратную теоремы и следующую схему:
Условие ® Заключение
Условие 1 ® Заключение 1
| Признак (прямая Th)
| Свойство (обратная Th)
| | Дано: DАВС,
ÐА=Ð С
Док-ть: АВ=ВС
| Дано: DАВС,
АВ=ВС
Док-ть: ÐА=Ð С
| | Дано: DАВС,
BL – медиана и высота
Док-ть: АВ=ВС
| Дано: DАВС,
АВ=ВС,
BL- биссектриса
Док-ть: BL- медиана и высота
| | Дано: DАВС,
BL – медиана и биссектриса
Док-ть: АВ=ВС
| Дано: DАВС,
АВ=ВС
BL- высота
Док-ть: BL- биссектриса и медиана
| | Дано: DАВС,
BL – биссектриса и высота
Док-ть: АВ=ВС
| Дано: DАВС,
АВ=ВС
BL- медиана
Док-ть: BL- биссектриса и высота
| Метрические соотношения в треугольнике
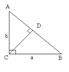
Синус Ða - оридината у т.М
Косинус Ða - абсцисса у т.М
0°£a£180°Þ0£sinx£1
-1£cosx£1

Тангенс Ða - отношение tga=  (a¹90°) (a¹90°)
Основное тригонометрическое тождество: sin2x+cos2x=1
Формулы приведения:
Sin(90-a)=cosa cos(90-a)=sina
Sin(180-a)=sina cos(180 -a)=-cosa
Теорема синусов: 
Теорема косинусов: a2=b2+c2-2bccosÐA
Теорема Пифагора – частный случай теоремы косинусов ÐА=90°Þ a2=b2+c2.
Решениетреугольников – нахождение элементов, определяющих треугольник.
Четырехугольники
Основные цели:
· Формирование у учащихся систематических сведений о четырехугольниках, их свойствах и признаках
· Формирование у учащихся первых представлений о фигурах, симметричных относительно точки и прямой.
Выпуклый четырехугольник – если он лежит по одну сторону от каждой прямой, проходящей через две соседние вершины.
| Выпуклый четырехугольник
2 пары ççсторон 1 пара çç нет çç сторон
      (парал-мы) (трапеции) (парал-мы) (трапеции)
Все стороны = все углы = общего вида
(ромб) (прамоуг.)
Равнобокие прямоугольные общего вида
1) Параллелограмм – четырехугольник, у которого противоположные стороны попарно параллельны.
| Признак (прямая Th)
| Свойство (обратная Th)
| | Дано: ABCD
AB=CD; BC=AD
Док-ть: AB||CD;DC||AD
| Дано: ABCD
AB||CD;DC||AD
Док-ть: AB=CD; BC=AD
| | Дано: ABCD
ÐА=Ð С
ÐB=Ð D
Док-ть: AB||CD;DC||AD
| Дано: ABCD
AB||CD;DC||AD
Док-ть: ÐА=Ð С
ÐB=Ð D
| | Дано: ABCD
AO=OC; OB=OD
Док-ть: AB||CD;DC||AD
| Дано: ABCD
AB||CD;DC||AD
Док-ть: AO=OC; OB=OD
|
2) Прямоугольник – четырехугольник, у которого все углы равны.
Из определения следует, что противоположные стороны параллельны, т.е. это параллелограмм.
Прямоугольник – параллелограмм, у которого один угол прямой.
Прямоугольник – параллелограмм, у которого диагонали равны.
3) Ромб – четырехугольник, у которого все стороны равны между собой.
По признаку параллелограмма следует, что ромб – параллелограмм.
Ромб – параллелограмм, у которого две смежные стороны равны.
Ромб – параллелограмм, у которого диагонали взаимно перпендикулярны.
Ромб – параллелограмм, у которого диагональ делит пополам каждый угол, через который она проходит.
4) Квадрат – четырехугольник, у которого все стороны равны между собой, и все углы прямые.
Значит, квадрат – частный вид прямоугольника и ромба.
5) Трапеция – четырехугольник, у которого две стороны параллельны, а две другие не параллельны.
Параллельные стороны – основания, непараллельные – боковые стороны.
Равнобокая трапеция – боковые стороны равны.
Прямоугольная трапеция – есть прямой угол.
В учебнике Погорелова трапеция рассматривается после параллелограммов и их частных видов. В учебнике Атанасяна – после параллелограммов.
Роль задач при изучении темы:
В задачный материал отнесено большое количество задач, которые можно отнести в теоретическую часть и обозначить за теорему. Нужно решить эти задачи, а результат использовать в дальнейшем.
1) Параллелограмм: Доказать, что биссектриса угла параллелограмма отделяет от него равнобедренный треугольник.
 Док-ть: АВ=ВС Док-ть: АВ=ВС
2) Ромб: Доказать, что если у параллелограмма диагонали перпендикулярны, то этот параллелограмм – ромб.
 Док-ть: АВ=АС Док-ть: АВ=АС
3) Прямоугольник: Прямоугольник вписан в равнобедренный прямоугольный треугольник
DАВС так, что прямой угол у них общий. Доказать, что периметр прямоугольника равен сумме катетов.
 Док-ть: 2АD+2AF=AB+AC Док-ть: 2АD+2AF=AB+AC
4) Трапеция: Доказать, что у равнобокой трапеции углы при основании равны.
 Док-ть: ÐА=Ð D Док-ть: ÐА=Ð D
| 2. Геометрия окружности
Данная тема изучается по частям на протяжении всего курса планиметрии (7-9 кл).
7 класс:
Впервые учащиеся знакомятся с окружностью при изучении геометрических построений.
Определение: Окружность – фигура, состоящая из всех точек плоскости, равноудаленных от данной точки. Эта точка называется центром окружности.
Элементы окружности: центр, радиус, хорда, диаметр.
· Окружность, описанная около треугольника
· Касательная к окружности (прямая, проходящая через точку окружности, перпендикулярно к радиусу)
· Окружность, вписанная в треугольник
· Задачи на построение (использование циркуля)
· Окружность – ГМТ, равноудаленных от данной точки.
8 класс:
· Уравнение окружности (х-а)2+(у-b)2=R2; O(a,b) – центр, R – радиус. x2+y2=R2 – окружность с центром в начале координат
· Взаимное расположение окружности и прямой x2+y2=R2 и x=d
R>d – 2 точки пересечения
R=d – 1 точка пересечения (прямая касается окружности)
R<d – нет точек пересечения - Æ
· Определение sin, cos, tg угла от 0° до 180° (используется окружность с центром (0;0) и радиусом R).
9 класс:
· Угол, вписанный в окружность, - угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Теорема: Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие1: Вписанные углы, опирающиеся на хорду (одну и ту же) и лежащие по одну сторону от нее, равны.
Следствие2: Углы, опирающиеся на диаметр, прямые.
· Пропорциональность отрезков хорд.
Теорема: Если хорды АВ и СD пересекаются в точке S, то AS×BS=CS×DS.
· Пропорциональность отрезков секущих
Теорема: если из точки Р к окружности провести 2 секущие, пересекающие окружность в точках A, B, C, D соответственно, то AP×BP=CP×DP.
· Теорема синусов
 , R – радиус, описанной около треугольника окружности.
· Теорема о свойстве вписанного четырехугольника (сумма противоположных углов равна 180°)
· Теорема о свойстве описанного четырехугольника (сумма длин противоположных сторон равна)
· Радиус окружности, описанной около правильного многоугольника: , R – радиус, описанной около треугольника окружности.
· Теорема о свойстве вписанного четырехугольника (сумма противоположных углов равна 180°)
· Теорема о свойстве описанного четырехугольника (сумма длин противоположных сторон равна)
· Радиус окружности, описанной около правильного многоугольника:
 · Радиус окружности, вписанной в правильный многоугольник:
· Радиус окружности, вписанной в правильный многоугольник:
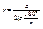 · Построение правильных многоугольников
· Длина окружности
Теорема: Отношение длины окружности С к ее диаметру D не зависит от окружности.
· Построение правильных многоугольников
· Длина окружности
Теорема: Отношение длины окружности С к ее диаметру D не зависит от окружности.
 Þ С=2pR=pD
· Радианная мера угла – отношение длины соответствующей дуги к радиусу окружности: Þ С=2pR=pD
· Радианная мера угла – отношение длины соответствующей дуги к радиусу окружности:  · Радиусы вписанной и описанной окружностей треугольника
· Радиусы вписанной и описанной окружностей треугольника
 ; ;  , S – площадь треугольника, a,b,c – стороны
· Круг – фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного.
Окружность-граница круга.
Теорема: Площадь круга Sкр= , S – площадь треугольника, a,b,c – стороны
· Круг – фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного.
Окружность-граница круга.
Теорема: Площадь круга Sкр=  · Scект.=
· Scект.=  (a-в радианах)
· Sсегм=Sсект-Sтреуг= (a-в радианах)
· Sсегм=Sсект-Sтреуг=  - -  = =  .
Замечание: поскольку материал, связанный с окружностью и кругом, распределен по программе, то целесообразно в конце 9 класса провести обобщенный урок для закрепления знаний учащихся.
3_2
2) a*b=b*a
3) (a+b)*c=ac+bc
Док-во: ac+bc =x1x3+y1y3+x2x3+y2y3=(x1+x2)x3+(y1+y2)y3
(a+b)c =(x1+x2)x3+(y1+y2)y3, след-но (a+b)c=ac+bc.
Решение геом. задач векторным методом состоит в следующем:
1) Условие и требование задачи переводится с геом. языка на векторный.
2) Средствами вект. алгебры условие задачи преобразуется так, чтобы получить соотношение, указанное в требовании задачи.
3) Полученное векторное соотношение истолковывается (интерпретируется) в исходных терминах.
Пр.
Док-ть, что отрезок, соединяющий середины диагоналей трапеции, паралл. основаниям и равен их полуразности. .
Замечание: поскольку материал, связанный с окружностью и кругом, распределен по программе, то целесообразно в конце 9 класса провести обобщенный урок для закрепления знаний учащихся.
3_2
2) a*b=b*a
3) (a+b)*c=ac+bc
Док-во: ac+bc =x1x3+y1y3+x2x3+y2y3=(x1+x2)x3+(y1+y2)y3
(a+b)c =(x1+x2)x3+(y1+y2)y3, след-но (a+b)c=ac+bc.
Решение геом. задач векторным методом состоит в следующем:
1) Условие и требование задачи переводится с геом. языка на векторный.
2) Средствами вект. алгебры условие задачи преобразуется так, чтобы получить соотношение, указанное в требовании задачи.
3) Полученное векторное соотношение истолковывается (интерпретируется) в исходных терминах.
Пр.
Док-ть, что отрезок, соединяющий середины диагоналей трапеции, паралл. основаниям и равен их полуразности.
 1) Дано: ◊АBCD, AD =
1) Дано: ◊АBCD, AD =  * BC, * BC,  >1
AK=KC, BN=ND.
Док-ть: MN =k* BC
│KN│= 1/2(│ AD │-│ BC │).
2) KN = AN - AK; AN =1/2(AB+AD); AK =1/2 AC.
KN =1/2(AB+AD-AC)=1/2(AD+CB)=1/2(AD-BC)
3) KN =1/2( >1
AK=KC, BN=ND.
Док-ть: MN =k* BC
│KN│= 1/2(│ AD │-│ BC │).
2) KN = AN - AK; AN =1/2(AB+AD); AK =1/2 AC.
KN =1/2(AB+AD-AC)=1/2(AD+CB)=1/2(AD-BC)
3) KN =1/2( BC-BC)= BC-BC)=  - ВС →KN|| BC
│ KN │=│1/2(AD-BC)│=1/2│ AD-BC │=1/2(│ AD│-
│BC │→KN=1/2(AD-BC). - ВС →KN|| BC
│ KN │=│1/2(AD-BC)│=1/2│ AD-BC │=1/2(│ AD│-
│BC │→KN=1/2(AD-BC).
| 3_1 Методика изучения темы «Векторы». Определение понятия вектора в различных школьных учебниках. Операции над векторами. Обучению векторному методу решения задач.
Во всех дейст-их учебниках есть материал по вект. алгебре. Эта тема важна как для шк. курса мат-ки, так и для межпредметных связей. Тема изуч-ся в 8-9 классе. Этого требует курс физики. Когда вводится понятие работы, уч-ся в курсе геометрии проходят скалярное произведение векторов (вектор силы на вектор перемещения).
Учебная цель: познакомить уч-ся с понятием вектора, основами вект. алгебры и научить применять вект. метод для реш-я задач.
Развивающая цель: развитие логич. мышления; раскрыть роль мат-ки через реш-е практич. задач из курса физики.
Материал излагается в 2-х частях:
1) 8 кл.: аффинные операции излагаются на геометрич. основе, т.е. «вектор- направленный отрезок».
2) 9 кл.: скалярное произв. векторов, основанное на координатах, т.е. «вектор- пара чисел».
Основное определение: «Вектор- направленный отрезок, т.е. отрезок, для которого указано, какой из его концов считается началом, а какой- концом».
Различ. подходы:
1) Вектор- напр. отрезок
2) Вектор- класс напр. отрезков, имеющих одинаковое направление и длину
3) Вектор- паралл. перенос.
При введении понятия вектора нужно идти от физич. примеров. В жизни мы встречаем вкличины, которые имеют своё значение (m,l,t и т. д). Но есть величины (V,S,a), которые характер. не только числ. значением, но и направлением. Эти величины наз-ся векторными.
 Два вектора коллинеарны, если онилежат на одной прямой или на паралл-х прямых.
Два вектора коллинеарны, если онилежат на одной прямой или на паралл-х прямых.
 
 a и b наз-ся равными, если 1) a ↑↑ b
2) │ a │=│ b │, (a и b -векторы).
Операции над векторами
1.Сложение векторов.
1) Пр-ло треуг-ка 2) Пр-ло параллелограмма
a и b наз-ся равными, если 1) a ↑↑ b
2) │ a │=│ b │, (a и b -векторы).
Операции над векторами
1.Сложение векторов.
1) Пр-ло треуг-ка 2) Пр-ло параллелограмма
  3) Коммутативность
a + b = b + a сим-ное постр-е пар-ма
3) Коммутативность
a + b = b + a сим-ное постр-е пар-ма
 4) Ассоциативность
(a + b)+ c = a +(b + c)
4) Ассоциативность
(a + b)+ c = a +(b + c)
  2. Вычитание векторов.
Вычесть из a вектор b - значит прибавить к a вектор, противоположный b, т.е. a-b=a+(-b).
2. Вычитание векторов.
Вычесть из a вектор b - значит прибавить к a вектор, противоположный b, т.е. a-b=a+(-b).
 3. Умножение вектора на число b=k*a.
1) k*(l* a)=(kl)* a
2) дистрибутивность относит. сложения чисел:
(k+l)* a =k* a +l* a
3) дистрибутивность относит. слож-я векторов:
k*(a + b)=k* a +k* b.
Докажем св-во 3)
1. случай: K>0. Выполним гомотетию (центр О; коэфф.k).
ОА| =k* ОА =k* a; ОВ| =k* ОВ =k* b
OC| = ОА| + ОВ| =k* OA +k* OB =k* a +k* b. (1).
Параллелограммы ОАСВ и ОА|B|C| подобны с коэфф. k, след-но, ∆ОАС~ ∆ОА|С| с коэф. k. по 2-му признаку подобия:
уголО-общий; угол ОАС=углу ОА|С|. Значит, ОС| = k* OC =k*(a + b) (2)
(1) и (2)следует k*(a+b)=k* a +k* b.
3. Умножение вектора на число b=k*a.
1) k*(l* a)=(kl)* a
2) дистрибутивность относит. сложения чисел:
(k+l)* a =k* a +l* a
3) дистрибутивность относит. слож-я векторов:
k*(a + b)=k* a +k* b.
Докажем св-во 3)
1. случай: K>0. Выполним гомотетию (центр О; коэфф.k).
ОА| =k* ОА =k* a; ОВ| =k* ОВ =k* b
OC| = ОА| + ОВ| =k* OA +k* OB =k* a +k* b. (1).
Параллелограммы ОАСВ и ОА|B|C| подобны с коэфф. k, след-но, ∆ОАС~ ∆ОА|С| с коэф. k. по 2-му признаку подобия:
уголО-общий; угол ОАС=углу ОА|С|. Значит, ОС| = k* OC =k*(a + b) (2)
(1) и (2)следует k*(a+b)=k* a +k* b.
 2-ой случай k<0. Аналогично.
2-ой случай k<0. Аналогично.
 4. Скалярное умножение:
a*b =│ a││b │*cos угла (a,b). В координатах: a (x1;y1); b =(x2;y2); c =(x3;y3).
a*b =x1*x2+y1*y2; a+b =(x1+x2; y1+y2)
1) a2=│a│2
4. Скалярное умножение:
a*b =│ a││b │*cos угла (a,b). В координатах: a (x1;y1); b =(x2;y2); c =(x3;y3).
a*b =x1*x2+y1*y2; a+b =(x1+x2; y1+y2)
1) a2=│a│2
|
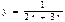 на отрезке [1; 8]
Знаменатель растет при росте аргумента Þ функция монотонно убывает.
Значит, у max =1/5 = y(1)
[ 1; 8]
Пр) Исследовать функцию и построить ее график
у = х – 3 +
на отрезке [1; 8]
Знаменатель растет при росте аргумента Þ функция монотонно убывает.
Значит, у max =1/5 = y(1)
[ 1; 8]
Пр) Исследовать функцию и построить ее график
у = х – 3 +  1.D(y) =
2.E(y) =
3.функция общего вида
4.непериодическая
5.
1.D(y) =
2.E(y) =
3.функция общего вида
4.непериодическая
5.  ;
;  D < 0 Þ нулей нет.
6. f(x) =
D < 0 Þ нулей нет.
6. f(x) =  x < 2 Þ f(x) < 0
7.x < 2, x ® 2 Þ f(x) ¯
x > 2, x ® 2 Þ f(x) ¯
x < 2 Þ f(x) < 0
7.x < 2, x ® 2 Þ f(x) ¯
x > 2, x ® 2 Þ f(x) ¯
 8.–
9.x ® 2, x < 2 Þ f(x) ® -¥
x ® 2, x > 2 Þ f(x) ® +¥ Þ x= 2 – вертик асимптота
10, 11. x ® +¥, х – 2® +¥ x ® -¥, х – 2® -¥
8.–
9.x ® 2, x < 2 Þ f(x) ® -¥
x ® 2, x > 2 Þ f(x) ® +¥ Þ x= 2 – вертик асимптота
10, 11. x ® +¥, х – 2® +¥ x ® -¥, х – 2® -¥
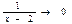
 х – 3 ® +¥ х – 3 ® -¥
f(x) > x - 3 f(x) < x - 3
х – 3 ® +¥ х – 3 ® -¥
f(x) > x - 3 f(x) < x - 3





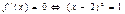


 (a¹90°)
(a¹90°)


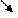





 (парал-мы) (трапеции)
(парал-мы) (трапеции) Док-ть: АВ=ВС
Док-ть: АВ=ВС Док-ть: АВ=АС
Док-ть: АВ=АС Док-ть: 2АD+2AF=AB+AC
Док-ть: 2АD+2AF=AB+AC Док-ть: ÐА=Ð D
Док-ть: ÐА=Ð D · Радиус окружности, вписанной в правильный многоугольник:
· Радиус окружности, вписанной в правильный многоугольник:
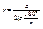 · Построение правильных многоугольников
· Длина окружности
Теорема: Отношение длины окружности С к ее диаметру D не зависит от окружности.
· Построение правильных многоугольников
· Длина окружности
Теорема: Отношение длины окружности С к ее диаметру D не зависит от окружности.
 Þ С=2pR=pD
· Радианная мера угла – отношение длины соответствующей дуги к радиусу окружности:
Þ С=2pR=pD
· Радианная мера угла – отношение длины соответствующей дуги к радиусу окружности:  · Радиусы вписанной и описанной окружностей треугольника
· Радиусы вписанной и описанной окружностей треугольника
 ;
;  , S – площадь треугольника, a,b,c – стороны
· Круг – фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного.
Окружность-граница круга.
Теорема: Площадь круга Sкр=
, S – площадь треугольника, a,b,c – стороны
· Круг – фигура, состоящая из всех точек плоскости, расстояние от которых до данной точки не больше данного.
Окружность-граница круга.
Теорема: Площадь круга Sкр=  · Scект.=
· Scект.=  (a-в радианах)
· Sсегм=Sсект-Sтреуг=
(a-в радианах)
· Sсегм=Sсект-Sтреуг=  =
=  .
Замечание: поскольку материал, связанный с окружностью и кругом, распределен по программе, то целесообразно в конце 9 класса провести обобщенный урок для закрепления знаний учащихся.
3_2
2) a*b=b*a
3) (a+b)*c=ac+bc
Док-во: ac+bc =x1x3+y1y3+x2x3+y2y3=(x1+x2)x3+(y1+y2)y3
(a+b)c =(x1+x2)x3+(y1+y2)y3, след-но (a+b)c=ac+bc.
Решение геом. задач векторным методом состоит в следующем:
1) Условие и требование задачи переводится с геом. языка на векторный.
2) Средствами вект. алгебры условие задачи преобразуется так, чтобы получить соотношение, указанное в требовании задачи.
3) Полученное векторное соотношение истолковывается (интерпретируется) в исходных терминах.
Пр.
Док-ть, что отрезок, соединяющий середины диагоналей трапеции, паралл. основаниям и равен их полуразности.
.
Замечание: поскольку материал, связанный с окружностью и кругом, распределен по программе, то целесообразно в конце 9 класса провести обобщенный урок для закрепления знаний учащихся.
3_2
2) a*b=b*a
3) (a+b)*c=ac+bc
Док-во: ac+bc =x1x3+y1y3+x2x3+y2y3=(x1+x2)x3+(y1+y2)y3
(a+b)c =(x1+x2)x3+(y1+y2)y3, след-но (a+b)c=ac+bc.
Решение геом. задач векторным методом состоит в следующем:
1) Условие и требование задачи переводится с геом. языка на векторный.
2) Средствами вект. алгебры условие задачи преобразуется так, чтобы получить соотношение, указанное в требовании задачи.
3) Полученное векторное соотношение истолковывается (интерпретируется) в исходных терминах.
Пр.
Док-ть, что отрезок, соединяющий середины диагоналей трапеции, паралл. основаниям и равен их полуразности.
 1) Дано: ◊АBCD, AD =
1) Дано: ◊АBCD, AD =  * BC,
* BC,  - ВС →KN|| BC
│ KN │=│1/2(AD-BC)│=1/2│ AD-BC │=1/2(│ AD│-
│BC │→KN=1/2(AD-BC).
- ВС →KN|| BC
│ KN │=│1/2(AD-BC)│=1/2│ AD-BC │=1/2(│ AD│-
│BC │→KN=1/2(AD-BC).
 Два вектора коллинеарны, если онилежат на одной прямой или на паралл-х прямых.
Два вектора коллинеарны, если онилежат на одной прямой или на паралл-х прямых.


 a и b наз-ся равными, если 1) a ↑↑ b
2) │ a │=│ b │, (a и b -векторы).
Операции над векторами
1.Сложение векторов.
1) Пр-ло треуг-ка 2) Пр-ло параллелограмма
a и b наз-ся равными, если 1) a ↑↑ b
2) │ a │=│ b │, (a и b -векторы).
Операции над векторами
1.Сложение векторов.
1) Пр-ло треуг-ка 2) Пр-ло параллелограмма

 3) Коммутативность
a + b = b + a сим-ное постр-е пар-ма
3) Коммутативность
a + b = b + a сим-ное постр-е пар-ма
 4) Ассоциативность
(a + b)+ c = a +(b + c)
4) Ассоциативность
(a + b)+ c = a +(b + c)

 2. Вычитание векторов.
Вычесть из a вектор b - значит прибавить к a вектор, противоположный b, т.е. a-b=a+(-b).
2. Вычитание векторов.
Вычесть из a вектор b - значит прибавить к a вектор, противоположный b, т.е. a-b=a+(-b).
 3. Умножение вектора на число b=k*a.
1) k*(l* a)=(kl)* a
2) дистрибутивность относит. сложения чисел:
(k+l)* a =k* a +l* a
3) дистрибутивность относит. слож-я векторов:
k*(a + b)=k* a +k* b.
Докажем св-во 3)
1. случай: K>0. Выполним гомотетию (центр О; коэфф.k).
ОА| =k* ОА =k* a; ОВ| =k* ОВ =k* b
OC| = ОА| + ОВ| =k* OA +k* OB =k* a +k* b. (1).
Параллелограммы ОАСВ и ОА|B|C| подобны с коэфф. k, след-но, ∆ОАС~ ∆ОА|С| с коэф. k. по 2-му признаку подобия:
уголО-общий; угол ОАС=углу ОА|С|. Значит, ОС| = k* OC =k*(a + b) (2)
(1) и (2)следует k*(a+b)=k* a +k* b.
3. Умножение вектора на число b=k*a.
1) k*(l* a)=(kl)* a
2) дистрибутивность относит. сложения чисел:
(k+l)* a =k* a +l* a
3) дистрибутивность относит. слож-я векторов:
k*(a + b)=k* a +k* b.
Докажем св-во 3)
1. случай: K>0. Выполним гомотетию (центр О; коэфф.k).
ОА| =k* ОА =k* a; ОВ| =k* ОВ =k* b
OC| = ОА| + ОВ| =k* OA +k* OB =k* a +k* b. (1).
Параллелограммы ОАСВ и ОА|B|C| подобны с коэфф. k, след-но, ∆ОАС~ ∆ОА|С| с коэф. k. по 2-му признаку подобия:
уголО-общий; угол ОАС=углу ОА|С|. Значит, ОС| = k* OC =k*(a + b) (2)
(1) и (2)следует k*(a+b)=k* a +k* b.
 2-ой случай k<0. Аналогично.
2-ой случай k<0. Аналогично.
 4. Скалярное умножение:
a*b =│ a││b │*cos угла (a,b). В координатах: a (x1;y1); b =(x2;y2); c =(x3;y3).
a*b =x1*x2+y1*y2; a+b =(x1+x2; y1+y2)
1) a2=│a│2
4. Скалярное умножение:
a*b =│ a││b │*cos угла (a,b). В координатах: a (x1;y1); b =(x2;y2); c =(x3;y3).
a*b =x1*x2+y1*y2; a+b =(x1+x2; y1+y2)
1) a2=│a│2
 Два вектора коллинеарны, если онилежат на одной прямой или на паралл-х прямых.
Два вектора коллинеарны, если онилежат на одной прямой или на паралл-х прямых.


 a и b наз-ся равными, если 1) a ↑↑ b
2) │ a │=│ b │, (a и b -векторы).
Операции над векторами
1.Сложение векторов.
1) Пр-ло треуг-ка 2) Пр-ло параллелограмма
a и b наз-ся равными, если 1) a ↑↑ b
2) │ a │=│ b │, (a и b -векторы).
Операции над векторами
1.Сложение векторов.
1) Пр-ло треуг-ка 2) Пр-ло параллелограмма
 3) Коммутативность
a + b = b + a сим-ное постр-е пар-ма
3) Коммутативность
a + b = b + a сим-ное постр-е пар-ма
 4) Ассоциативность
(a + b)+ c = a +(b + c)
4) Ассоциативность
(a + b)+ c = a +(b + c)
 2. Вычитание векторов.
Вычесть из a вектор b - значит прибавить к a вектор, противоположный b, т.е. a-b=a+(-b).
2. Вычитание векторов.
Вычесть из a вектор b - значит прибавить к a вектор, противоположный b, т.е. a-b=a+(-b).
 3. Умножение вектора на число b=k*a.
1) k*(l* a)=(kl)* a
2) дистрибутивность относит. сложения чисел:
(k+l)* a =k* a +l* a
3) дистрибутивность относит. слож-я векторов:
k*(a + b)=k* a +k* b.
Докажем св-во 3)
1. случай: K>0. Выполним гомотетию (центр О; коэфф.k).
ОА| =k* ОА =k* a; ОВ| =k* ОВ =k* b
OC| = ОА| + ОВ| =k* OA +k* OB =k* a +k* b. (1).
Параллелограммы ОАСВ и ОА|B|C| подобны с коэфф. k, след-но, ∆ОАС~ ∆ОА|С| с коэф. k. по 2-му признаку подобия:
уголО-общий; угол ОАС=углу ОА|С|. Значит, ОС| = k* OC =k*(a + b) (2)
(1) и (2)следует k*(a+b)=k* a +k* b.
3. Умножение вектора на число b=k*a.
1) k*(l* a)=(kl)* a
2) дистрибутивность относит. сложения чисел:
(k+l)* a =k* a +l* a
3) дистрибутивность относит. слож-я векторов:
k*(a + b)=k* a +k* b.
Докажем св-во 3)
1. случай: K>0. Выполним гомотетию (центр О; коэфф.k).
ОА| =k* ОА =k* a; ОВ| =k* ОВ =k* b
OC| = ОА| + ОВ| =k* OA +k* OB =k* a +k* b. (1).
Параллелограммы ОАСВ и ОА|B|C| подобны с коэфф. k, след-но, ∆ОАС~ ∆ОА|С| с коэф. k. по 2-му признаку подобия:
уголО-общий; угол ОАС=углу ОА|С|. Значит, ОС| = k* OC =k*(a + b) (2)
(1) и (2)следует k*(a+b)=k* a +k* b.
 2-ой случай k<0. Аналогично.
2-ой случай k<0. Аналогично.

 1) Дано: ◊АBCD, AD =
1) Дано: ◊АBCD, AD =  Понятие «ур-е линии» легче всего ввести на примере прямой у=х. Если х=у, то точка принадлежит линии, иначе – нет.
Опр.Урав-м линии в дек-ых корд-х наз-ся уравнение с 2мя переменными f(x,y)=0, удовлетворяющее след.-м условиям:
1) если точка имеет корд-ы, удовлет-е данному ур-ю, то она Î линии; 2) если точка имеет корд., не удовлет-е данному ур-ю, то она Ï линии.
Понятие «ур-ие линии» служит основой для вывода ур-я окруж. и пряиой.
Вывод ур-я окружности.
Понятие «ур-е линии» легче всего ввести на примере прямой у=х. Если х=у, то точка принадлежит линии, иначе – нет.
Опр.Урав-м линии в дек-ых корд-х наз-ся уравнение с 2мя переменными f(x,y)=0, удовлетворяющее след.-м условиям:
1) если точка имеет корд-ы, удовлет-е данному ур-ю, то она Î линии; 2) если точка имеет корд., не удовлет-е данному ур-ю, то она Ï линии.
Понятие «ур-ие линии» служит основой для вывода ур-я окруж. и пряиой.
Вывод ур-я окружности.
 Опр. Окр-ть – ГМТ, состоящее из всех точек пл-ти, удаленных на зад. расстоянии от фиксир-й точки.
Дано: w(О;R);O(х0;у0). Вывести ур-ие w.
"А(х,у)Îw, если ОА=R. (1)
Запишем (1) в корд-х:
ОА=
Опр. Окр-ть – ГМТ, состоящее из всех точек пл-ти, удаленных на зад. расстоянии от фиксир-й точки.
Дано: w(О;R);O(х0;у0). Вывести ур-ие w.
"А(х,у)Îw, если ОА=R. (1)
Запишем (1) в корд-х:
ОА=  (2)
(2)®(1) и возведем в квадрат:
(х-х0)+(у-у0)=R2. (3)
Получили ур-е с 2мя переем-ми®это ур-е линии.
т.АÎwÞее корд.удовл-т ур-ю (3)
т.N(x1,у1)ÏwÞее корд.не удовл-т ур-ю (3)
(x¢-x0)(y¢-y0)¹R2, т.к. ON¹R.
На основании опред-я «ур-е линии» делаем вывод, что (3)–это ур-е окр-ти с центром в т.О(х0,у0) и радиусом R.
Вопросы на понимание.
1)Как опред-ть,Î ли точка с дан-ми корд. данной линии, заданной ур-ем?
2)Какие данные нужны, чтобы зап-ть ур-е окр-ти?
3)укажите центр и рад-с окр-ти, заданной Ур-ем.
4)прочитать график и написать ур-е окр-ти.
5)изобр-ть окр-ть на корд-й пл-ти.
Пр-р(корд-й метод реш-я задач):
(2)
(2)®(1) и возведем в квадрат:
(х-х0)+(у-у0)=R2. (3)
Получили ур-е с 2мя переем-ми®это ур-е линии.
т.АÎwÞее корд.удовл-т ур-ю (3)
т.N(x1,у1)ÏwÞее корд.не удовл-т ур-ю (3)
(x¢-x0)(y¢-y0)¹R2, т.к. ON¹R.
На основании опред-я «ур-е линии» делаем вывод, что (3)–это ур-е окр-ти с центром в т.О(х0,у0) и радиусом R.
Вопросы на понимание.
1)Как опред-ть,Î ли точка с дан-ми корд. данной линии, заданной ур-ем?
2)Какие данные нужны, чтобы зап-ть ур-е окр-ти?
3)укажите центр и рад-с окр-ти, заданной Ур-ем.
4)прочитать график и написать ур-е окр-ти.
5)изобр-ть окр-ть на корд-й пл-ти.
Пр-р(корд-й метод реш-я задач):
 Найти: МА2+МВ2+МС2+MD2–?
М–точка Î окр-ти.
Реш-е: пусть М(х,у). Запишем треб-ие задачи в корд-ах:
МА2+МВ2+МС2+MD2=(-1-х)2+у2+(-1-х)2+(2-у)2+(1-х)2+(2-у)2+(1-х)2+у2=2(х+1)2+2(х-1)2+2(у-2)2+2у2=2х2+4х+2+2х2-4х+2+2у2-8у+8+2у2 = 4х2 + 4у2-8у+12. (1)
Ур-е окр-ти с центром О1(0;1) и радиусом 1: (х-0)2+(у-1)2=1; х2=1-(у-1)2Þх2=2у-у2. (2)
Подставили (2) в (1):
МА2+МВ2+МС2+MD2=4(2у-у2)+4у2-8у+12=12.
Ответ: 12.
Найти: МА2+МВ2+МС2+MD2–?
М–точка Î окр-ти.
Реш-е: пусть М(х,у). Запишем треб-ие задачи в корд-ах:
МА2+МВ2+МС2+MD2=(-1-х)2+у2+(-1-х)2+(2-у)2+(1-х)2+(2-у)2+(1-х)2+у2=2(х+1)2+2(х-1)2+2(у-2)2+2у2=2х2+4х+2+2х2-4х+2+2у2-8у+8+2у2 = 4х2 + 4у2-8у+12. (1)
Ур-е окр-ти с центром О1(0;1) и радиусом 1: (х-0)2+(у-1)2=1; х2=1-(у-1)2Þх2=2у-у2. (2)
Подставили (2) в (1):
МА2+МВ2+МС2+MD2=4(2у-у2)+4у2-8у+12=12.
Ответ: 12.
 – So=1 ед2
Св-ва 1-4 при этом подходе не док-ся, а вводятся как аксиомы.
Этот подход имеет недостаток: понятие площади опирается на понятие квардрир. Фигуры, а оно, в свою очередь, на понятие площади фигуры.
Полная формулировка понятие площади:
1)Площадь определяется как фун-я, обладающая св-вами 1-4 для многоугольной фигуры.
2)Определяется класс квадрир.фигур
3)Площадь – фун-я со св-вами 1-4 на классе квадрир. Ф-р.
При аксиоматич. подходе нужно док-ть теорему: Ф-ция со св-ваи 1-4 сущ-ет и единственна.
Все остальные св-ва площади док-ся на основе определения.
ПР:Если фигура Q содержится в фигуре R, то площадь Q меньше площади R, т.е. QÌRÞS(Q)<S(R) – св-во монотонности.
2.
– So=1 ед2
Св-ва 1-4 при этом подходе не док-ся, а вводятся как аксиомы.
Этот подход имеет недостаток: понятие площади опирается на понятие квардрир. Фигуры, а оно, в свою очередь, на понятие площади фигуры.
Полная формулировка понятие площади:
1)Площадь определяется как фун-я, обладающая св-вами 1-4 для многоугольной фигуры.
2)Определяется класс квадрир.фигур
3)Площадь – фун-я со св-вами 1-4 на классе квадрир. Ф-р.
При аксиоматич. подходе нужно док-ть теорему: Ф-ция со св-ваи 1-4 сущ-ет и единственна.
Все остальные св-ва площади док-ся на основе определения.
ПР:Если фигура Q содержится в фигуре R, то площадь Q меньше площади R, т.е. QÌRÞS(Q)<S(R) – св-во монотонности.
2.



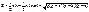








 Док-ть:
Док-ть:




 l || AB;
l || AB; SAC1B=SAC2B=SAC3B=…
SAC1B=SAC2B=SAC3B=…
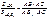

 Площ-дь круга. Чтобы выч-ть S круга, нужно допол-ть опред-е S фиг-ры. Фиг-ра Ф имеет пл-дь S, если $ сод-щие ее прост-е фигуры и сод-иеся в ней простые фигуры с площ-ми, как угодно мало отлич-ся от S.
Площ-дь круга. Чтобы выч-ть S круга, нужно допол-ть опред-е S фиг-ры. Фиг-ра Ф имеет пл-дь S, если $ сод-щие ее прост-е фигуры и сод-иеся в ней простые фигуры с площ-ми, как угодно мало отлич-ся от S.

 Если n®¥, p®C=2pR;
Если n®¥, p®C=2pR;  Значит, S1®pR2; S2®pR2;
По введённому определению площади получаем, что площадь круга Sкр=pR2
Площадь сектора
Значит, S1®pR2; S2®pR2;
По введённому определению площади получаем, что площадь круга Sкр=pR2
Площадь сектора