Интеграл Коши и интеграл типа Коши.

Представление любой голоморфной функции комплексного переменного в виде интеграла Коши по контуру сыграло важную роль в развитии теории аналитических функций.

Интеграл от функции комплексного переменного z=x+iy вдоль ориентированной спрямляемой кривой может быть определен формулой .

Напомним, кривая – это класс эквивалентных путей. Спрямляемый путь – такое непрерывное отображение отрезка в комплексную плоскость, что почти всюду на существует производная абсолютно интегрируемая по Лебегу, то есть существует интеграл Лебега – длина пути. По определению два пути и эквивалентны, если существует непрерывная возрастающая функция такая, что 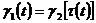для всех .

Центральное место в теории аналитических функций занимает интегральная теорема Коши: если – аналитическая функция в области D, то 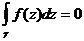для любой замкнутой кривой 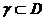, ограничивающей область, лежащую в D. Верно и обратное утверждение (теорема Мореры): если – непрерывна в D и для любой такой кривой , то – аналитическая функция в области D.

Интегральная теорема Коши позволяет получить интегральную формулу Коши, выражающую значения аналитической функции внутри области через её значения на границе этой области: , 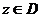; здесь D – область (открытое связное множество), граница которой состоит из конечного числа непересекающихся спрямляемых кривых (ориентация предполагается положительной относительно области D, то есть область остается слева при обходе границы), – функция, аналитическая в некоторой области 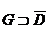. Эта формула позволяет, в частности, свести изучение многих вопросов, связанных с аналитическими функциями к соответствующим вопросам для простейшей функции – ядра Коши , , .

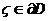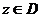Впервые интегральная формула Коши появилась применительно к частным случаям в его работе 1823 году. Правая часть этой формулы называется интегралом Коши. Интеграл Коши характеризуется двумя условиями:

1. Интеграл Коши берется по замкнутой гладкой или хотя бы кусочно-гладкой кривой .

2. Подынтегральная функция имеет вид , где , а –однозначная аналитическая функция на и внутри .

При этих условиях интеграл Коши 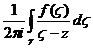задает аналитическую функцию переменного z во всей комплексной плоскости, кроме точек контура : 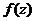внутри контура и этот интеграл равен нулю во внешности контора .

Если, с другой стороны, 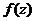является однозначной аналитической функцией в неограниченной области – внешности замкнутой кривой и на , имеет конечный , то справедлива интегральнаяформула Коши для неограниченной области: = (обход по-прежнему против часовой стрелки).

Пусть теперь – некоторая, не обязательно замкнутая, кусочно-гладкая кривая, расположенная в конечной плоскости, – непрерывная комплексная функция на и z – точка, не лежащая на . Интегралом типаКоши называется обобщение интеграла Коши в виде: , где . Функцию называют плотностью интеграла типа Коши.

Простейшие свойства интеграла типа Коши:

1. - однозначная аналитическая функция переменного z в С \ .

2. Производные выражаются формулами , ,

3. при .

4. При 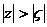– сумма бесконечно убывающей геометрической прогрессии. Поскольку кривая ограничена, , то при достаточно больших значениях справедливо разложение интеграла типа Коши , где .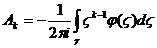

Пример. Пусть – простая кусочно-гладкая разомкнутая дуга ab, . Тогда для , где под понимается ветвь, голоморфная на разрезанной вдоль ab плоскости, исчезающая на бесконечности со скоростью : .

С точки зрения общей теории аналитических функций и применений к механике и физике основное значение имеет вопрос о существовании граничных значений интеграла типа Коши при приближении z к и об их аналитическом выражении.

Рассмотрим сначала предельные значения в точках контура интеграла Коши, то есть когда функция является аналитической на контуре и внутри него. В этом случае, очевидны предельные значения: и .

Далее будем использовать для предельных значений функции обозначения – изнутри и – извне контура . Итак, для интеграла Коши = 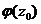– непрерывная функция на , =0 – тоже непрерывная на функция.

Для интеграла типа Коши общего вида дело обстоит несколько сложнее. Пусть кривая задана уравнением , – длина её дуги, отсчитываемая от какой-либо фиксированной точки, – произвольная фиксированная точка на и – часть кривой , которая остается от после удаления из дуги с концами и . Если существует конечный предел 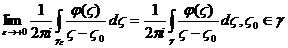, то он называется сингулярным интегралом. Фактически это интеграл в смысле главного значения. Доказано, что он существует, если кривая гладкая в окрестности точки 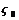, точка не является концом , а функция удовлетворяет условию Гёльдера в окрестности .

Определение. Функция удовлетворяет условию Гёльдера порядка на множестве M, если существуют две положительные константы С и такие, что для всех .

Оказывается, если в окрестности неконцевой точки выполнены указанные условия на кривую и функцию , то существуют предельные граничные значения интеграла типа Коши, которые выражаются формулами Сохоцкого-Племеля:

.

При этом функции и непрерывны в окрестности соответственно изнутри и извне контура .

В случае интеграла Коши сингулярный интеграл в точке контура 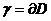равен , так как формулы Сохоцкого-Племеля в этом случае имеют вид

и, в то же время для интеграла Коши мы знаем предельные значения: , .

Формулы Сохоцкого-Племеля для интеграла типа Коши иногда записывают в эквивалентной форме:

,

, .

Формулы Сохоцкого-Племеля имеют основное значение при решении граничных задач в теории аналитических функций, сингулярных интегральных уравнений, связанных с интегралом типа Коши, а также при решении ряда задач гидродинамики, теории упругости и других разделов теоретической и прикладной математики.

Значение интеграла типа Коши на линии интегрирования [5].

Пусть , удовлетворяет условию Гёльдера в окрестности точки на . Покажем, что в этом случае главное значение интеграла типа Коши существует и найдём его выражение через интеграл в обычном смысле. Считаем, что дуга = ab разомкнута. Рассмотрим

.

Поскольку вблизи справедлива оценка , , то предел первого интеграла справа существует и равен несобственному интегралу в обычном смысле . Вычислим предел при второго интеграла. Для этот интеграл вычисляется в конечном виде. Чтобы точно определить значения логарифмических членов, которые появятся при этом вычислении, поступим следующим образом. Опишем из , как из центра, дугу окружности радиуса 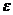, проходящую через точки и , расположенную справа от :

Пусть обозначает простую дугу , а – дугу окружности. Тогда

. Теперь не лежит на , поэтому согласно рассмотренному примеру

– значение, принимаемое в точке той ветвью функции , которая голоморфна на разрезанной вдоль плоскости и исчезает на бесконечности. Это равносильно значению, принимаемому слева от в точке той ветвью, которая голоморфна на разрезанной вдоль плоскости и исчезает на бесконечности.

Дале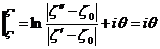е, = , где – изменение аргумента 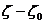при перемещении из положения в положение вдоль дуги . Очевидно, что .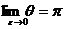

Итак, все пределы при существуют, что доказывает существование интеграла в смысле главного значения для . Это главное значение даётся формулой

,

где – значение, принимаемое слева от функцией , голоморфной на разрезанной вдоль = ab плоскости и исчезающей на бесконечности. В частности, .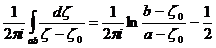

В приложениях часто – отрезок вещественной оси 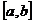. Выберем в этом случае ветви

и

так, чтобы в плоскости с вырезанным отрезком 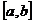функция исчезала на бесконечности.

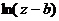Возьмём и . При таком выборе аргументов обе функции и 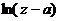голоморфны и однозначны на всей комплексной плоскости с разрезом , а их разность однозначна на плоскости с вырезанным отрезком 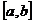, так как на луче разность имеет одинаковые предельные значения по обоим берегам разреза. На верхнем берегу разреза вдоль отрезка 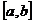имеем , , поэтому здесь . На нижнем берегу разреза вдоль отрезка 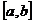, , поэтому здесь .

Покажем, что при указанном выборе аргументов функция исчезает при . Очевидно, что вещественная часть этой функции при . Покажем, что при .

Пусть , , .

при ,

что легко показать с помощью теоремы косинусов:

при .

Пусть теперь , ,

. .

С учётом теоремы косинусов при .

Итак, для отрезка вещественной оси 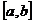ветви логарифмов выбраны так, что при . При этом в точке значение этой функции, принимаемое слева, то есть сверху от отрезка , равно . Подставим это значение в полученное представление :

.

Здесь слагаемое 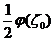сократилось.

Для гладкой части кривой справедлива

Теорема[5]. Если плотность удовлетворяет условию Гёльдера на некоторой гладкой части линии , то интеграл типа Коши определяет функцию, непрерывно продолжимую слева и справа на эту часть за исключением, быть может, её концов. Предельные значения имеют вид

слева от ,

справа от ,

где понимается в прежнем смысле.

Эти формулы для предельных значений интеграла типа Коши неудобны тем, что непосредственно применимы лишь к случаю, когда – простая разомкнутая дуга. Если же рассматривать главное значение интеграла типа Коши, то эти формулы приводятся к более простому виду, притом пригодному для любой кусочно-гладкой линии интегрирования:

.

.

Это формулы Сохоцкого-Племеля, справедливые для любой кусочно-гладкой линии, при условии, что точка отлична от узлов (в том числе концов), а удовлетворяет условию Гёльдера в окрестности .

Эти формулы обобщаются для разности предельных значений

в случае, когда в точке всего лишь непрерывна, но предел здесь понимается в следующем смысле. Через точку проводится произвольная прямая , не являющаяся касательной к кривой в точке . На этой прямой берутся две точки и соответственно слева и справа на равных расстояниях от . Здесь полагают по определению .