4.1. Несобственные интегралы первого рода (с бесконечными пределами)
Пусть дан интеграл с фиксированным нижним пределом интегри-рования а
.
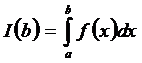Рассмотрим его поведение при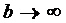 
.
Определение 1. Если существует конечный предел 
, то этот предел называется несобственным интегралом первого рода от функции 
на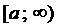 
и обозначается
(1)
В этом случае интеграл называется сходящимся. Если же предел (1) не существует или равен бесконечности, то такой интеграл называется расходящимся.
Аналогично определяются несобственные интегралы и для других бесконечных интервалов:
.
Если известна первообразная функции , то
(2)
Пример 1. Исследовать сходимость интеграла 
.
По формуле (2) получаем
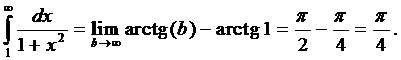
Пример 2. Исследовать сходимость интеграла 
Согласно определению несобственного интеграла из таблицы неопре-делённых интегралов получим
Таким образом, интеграл сходится, если степень 
и расходится, если 
.
Если первообразная функции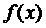 
не известна, то при исследовании несобственного интеграла на сходимость применяют признаки сравнения:
Теорема 1. Пусть 
, тогда
- если 
сходится, то сходится и 
,
- если расходится, то расходится и .
В силу свойства определённого интеграла, интегрируя данное нера-венство, получаем
.
Переходя к пределу при 
, приходим к неравенству
Аналогично доказывается вторая часть теоремы.
Пример 3. Исследовать на сходимость 
.
Таким образом, интеграл сходится. Неравенство было получено с использованием свойства 7 об оценке интеграла.
Теорема 2. Если 
.
Доказательство аналогичное.
В этом случае интеграл называется абсолютно сходящимся. Если 
, а 
расходится, то интеграл называется условно сходящимся.
Например, интеграл 
является абсолютно сходящимся, так как
Интеграл 
- условно сходящийся.
4.2. Несобственные интегралы второго рода (от разрывных функций)
Если функция на 
имеет конечное число точек разрыва первого рода, то вычисление интеграла от такой функции трудности не представляет. Например, если 
- точка разрыва первого рода, тогда
Если же функция имеет бесконечный разрыв, то в этом случае интеграл называется несобственным второго рода. Тогда, если 
- точка разрыва второго рода, то интеграл определяется следующим образом
Аналогично определяются несобственные интегралы от функций с разрывами в точках 
и :
Если для несобственного интеграла от разрывной функции в точке известна первообразная 
, то его сходимость зависит от существования значения 
.
Пример 4. Исследовать сходимость 
.
Таким образом, интеграл сходится, если степень 
и расходится, если 
.
Если же первообразная функции не известна, то для исследования сходимости, как и для несобственных интегралов первого рода, исполь-зуются аналогичные признаки сравнения.
Пример 5. Исследовать на сходимость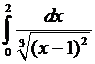 
.
Замечаем, что в точке 
подынтегральная функция имеет разрыв второго рода и тогда
Интеграл сходится.