МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО СПЕЦИАЛЬНОГО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
ТАШКЕНТСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ
УНИВЕРСИТЕТ имени НИЗАМИ
Решение неравенств
(методические рекомендации для учителей)
БАКИРОВА А.Ю.
НОРМАТОВ А.А.
Ташкент 2004
Решение неравенств один из самых трудных для понимания и усвоения разделов в курсе школьной алгебры. Вообще для решения неравенств существует множество различных методов, как-то: метод системосовокупностей (с.с.), метод интервалов, графический метод, а также нестандартные методы.
В школе, в лучшем случае, делается попытка научить учащихся решать неравенства методом с.с, что в силу сложности этого метода, очень редко удается. Среди учителей встречается неправильное мнение о том, что неравенства можно решать подобно уравнениям, учитывая при этом область допустимых значений (ОДЗ).
В школьном курсе математики рассматривается метод интервалов для дробно-рациональных неравенств, графический метод рассматривается недостаточно. А о нестандартных методах говорить не приходится. При этом обучение строится по принципу «правило-пример», для выполнения упражнений учащимся достаточно знаний некоторых правил и образца показанного учителем. Такой подход отучает от самостоятельного мышления, не способствует развитию математической деятельности.
Учитывая эти недостатки средней школы, рассмотрим методический подход изучения темы «Неравенства» на более высоком уровне в академических лицеях математического и естественного направления.
Предлагаемый подход позволяет освободить учащихся от необходимости держать постоянно в памяти большое количество второстепенных формул, теорем, методов и тем самым предоставит им возможность для активного восприятия материала, для формирования своей индивидуальной системы знаний.
ОПИСАНИЕ МЕТОДОВ РЕШЕНИЯ НЕРАВЕНСТВ
Метод системосовокупностей
Метод системосовокупностей один из самых распространенных и универсальных методов решения неравенств любого типа, т.к. метод системосовокупностей (с.с.) подчинен законам теории множеств.
Однако бывают и исключения, которые объясняются лишь тем, что какие-то неравенства нельзя решить методами курса математики лицея.
Например,

В дальнейшем будем показано, что такие неравенства решаются методом интервалов.
Системосовокупностью будем называть любое множество уравнений и неравенств с неизвестными  связанных между собой логическими знаками
связанных между собой логическими знаками  (система) и
(система) и  (совокупность). В дальнейшем будем обозначать с.с. большими латинскими буквами
(совокупность). В дальнейшем будем обозначать с.с. большими латинскими буквами  .
.
Решением с.с.  называется множество
называется множество  всех таких наборов действительных чисел
всех таких наборов действительных чисел  , каждый из которых удовлетворяет с.с.
, каждый из которых удовлетворяет с.с.  . Набор
. Набор  удовлетворяет с.с.
удовлетворяет с.с.  тогда и только тогда, когда он удовлетворяет хотя бы одной из с.с.
тогда и только тогда, когда он удовлетворяет хотя бы одной из с.с.  и
и  . Таким образом, записи
. Таким образом, записи 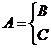 и
и  , а также
, а также  и
и  имеют одинаковый смысл.
имеют одинаковый смысл.
Далее, записи  (
( равносильно или эквивалентно
равносильно или эквивалентно  ) и
) и  (
( влечет
влечет  или из
или из  следует
следует  ) означают соответственно, что
) означают соответственно, что  или
или  .
.
Отметим некоторые правила преобразования с.с.
1.1  ;
;
1.2  ;
;
1.3.  где
где  - логический знак отрицания.
- логический знак отрицания.
1.4.  ;
;
1.5. 
которые основаны соответственно на следующих соотношениях теории множеств:

где  - дополнение к
- дополнение к  .
.
Отметим также, что если  , т.е.
, т.е.  , то
, то  и
и  , т.к. прим этом
, т.к. прим этом  и
и  .
.
Разберем пример.
1. 
Для решения этого неравенства используем правило (1.3.).
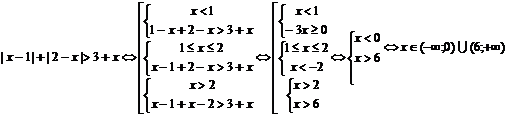
При решении неравенств методом с.с. исходное неравенство заменяем на равносильную ему с.с., учитывая при этом теоретико-множественные правила, а также функциональное строение неравенства.
Приведем несколько наиболее употребимых переходов от неравенств к эквивалентным с.с.
Начнем с неравенств содержащих знак абсолютной величины.
2.1  ;
;
2.2. а)  ;
;
2.2 б)  ;
;
Решим несколько примеров.
2. 
Ответ: 
3.

Ответ: 
Рассмотрим простейшие иррациональные неравенства.
При решении иррациональных неравенств методом с.с. исходное неравенство сводится к равносильной с.с. рациональных неравенств.
3.1.  ;
;
3.2.  ;
;
3.3.  ;
;
3.4.  ;
;
3.5.  ;
;
3.6.  .
.
Примеры.
4. 
(т.к. 
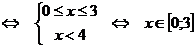 .
.
Ответ:  .
.
5.  .
.
Ответ:  .
.
Показательно-степенные неравенства.
В силу монотонности показательной функции переход от неравенства к с.с. будет следующим.
4.1. 
Возможны частные случаи, когда  и
и 
4.1.а) 
4.1.б) 
Примеры.
6.  .
.
Ответ:  .
.
7. 
 .
.
Ответ:  .
.
Логарифмические неравенства.
5.1 
Возможны частные случаи, когда
 .
.
5.1.а)

5.1.б)

5.1.в)

Примеры.
8. 
 .
.
Ответ:  .
.
9.  .
.
Ответ:  .
.
10. 
 .
.
Ответ:  .
.
11. 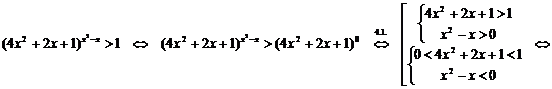
 .
.
Ответ:  .
.
12.  .
.
Ответ:  .
.
Метод интервалов
Метод интервалов также принадлежит к числу наиболее употребимых методов.
В школьном курсе математики этот метод рассматривается только для дробно-рациональных функций.
Рассмотрим обобщенный метод интервалов – его теорию и применение.
Пусть  , где
, где  - функции из
- функции из  с областями определения
с областями определения  в
в  соответственно.
соответственно.
Тогда  .
.
Обозначим также  и положим
и положим  . Пусть
. Пусть  , где
, где  - множество попарно непересекающихся интервалов, причем такое, что для всякого
- множество попарно непересекающихся интервалов, причем такое, что для всякого  интервал
интервал 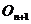 расположен на оси
расположен на оси  правее интервала
правее интервала  . Кроме того, предполагаем, что каждая из функций
. Кроме того, предполагаем, что каждая из функций  сохраняет постоянный знак на каждом интервале из
сохраняет постоянный знак на каждом интервале из  . Это обеспечивается, например, условием непрерывности этих функций на
. Это обеспечивается, например, условием непрерывности этих функций на  .
.
Идея излагаемого метода основывается на следующих двух положениях:
1) Функция сохраняет постоянный знак на каждом интервале из  .
.
2) при переходе от интервала  к интервалу
к интервалу 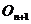 функция
функция  сохраняет (меняет) свой знак, если четное (нечетное) число функций из
сохраняет (меняет) свой знак, если четное (нечетное) число функций из  меняет свой знак при переходе.
меняет свой знак при переходе.
В самом деле, знак  на интервале
на интервале  определяется количеством функций из
определяется количеством функций из  , которые отрицательны на
, которые отрицательны на  и, очевидно, совпадает (противоположен) знаку
и, очевидно, совпадает (противоположен) знаку  на интервале
на интервале 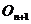 , если это количество изменяется на четное (нечетное) число при переходе от
, если это количество изменяется на четное (нечетное) число при переходе от  к
к 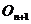 .
.
Таким образом, решение неравенства  , где
, где  означает один из знаков
означает один из знаков  , сводится к нахождению множества
, сводится к нахождению множества 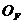 , т.е. хотя бы на одном из интервалов
, т.е. хотя бы на одном из интервалов  , и к применению описанной процедуры рассмотрения знаков на все оставшиеся интервалы. Заметим только, что если
, и к применению описанной процедуры рассмотрения знаков на все оставшиеся интервалы. Заметим только, что если  совпадает с одним из знаков
совпадает с одним из знаков  или
или  , то объединение соответствующих интервалов необходимо пополнить множеством
, то объединение соответствующих интервалов необходимо пополнить множеством 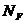 .
.
Итак, применение изложенного метода позволяет, фактически, свести решение неравенства  к нахождению областей определения функций
к нахождению областей определения функций  и к решению уравнений
и к решению уравнений  . Также этот метод позволяет, с одной стороны, значительно расширить круг неравенств, поддающихся простому решению, а с другой – упростить решение многих неравенств. Так, например, когда в рассмотренном произведении стоит всего одна функция, удается избавиться от необходимости соблюдать равносильность в процессе решения соответствующих неравенств, что, в свою очередь, позволяет избежать большого числа распространенных ошибок. В случае, когда в произведении стоит более двух функций, применение обобщенного метода интервалов наиболее эффективно тогда, когда выяснение знаков функций в произведении, стоящих в левой части рассматриваемого неравенства, не составляет труда.
. Также этот метод позволяет, с одной стороны, значительно расширить круг неравенств, поддающихся простому решению, а с другой – упростить решение многих неравенств. Так, например, когда в рассмотренном произведении стоит всего одна функция, удается избавиться от необходимости соблюдать равносильность в процессе решения соответствующих неравенств, что, в свою очередь, позволяет избежать большого числа распространенных ошибок. В случае, когда в произведении стоит более двух функций, применение обобщенного метода интервалов наиболее эффективно тогда, когда выяснение знаков функций в произведении, стоящих в левой части рассматриваемого неравенства, не составляет труда.
Прейдем к разбору примеров:
13. 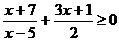
Приведем к общему знаменателю, тогда исходное неравенство примет вид


После проверки: 



Ответ: 
Отметим, что метод интервалов рассматриваемый в школьном курсе математики является частным случаем рассмотренного выше обобщенного метода интервалов.
Рассмотрим пример:
14. 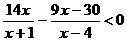
Приведем к общему знаменателю, тогда наше неравенство примет вид:

На числовой прямой отмечаем нули числителя и знаменателя
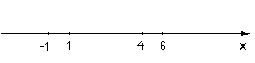
на одном из полученных интервалов определяем знак

Затем расставляем знаки на интервалах, учитывая при этом кратность нулей.

Таким образом, решением нашего неравенства будем:  .
.
Ответ:  .
.
Также отметим, что в дальнейшем рациональные неравенства будем решать по этой упрощенной схеме.
Необходимо также заметить, что если в рациональном неравенстве поставить вместо переменной какую-либо монотонную функцию от этой переменной, то можно решать неравенство методом интервалов по рассмотренной выше упрощенной схеме.
Например:
15. 
Найдем нули


Ответ:  .
.
16. 


Проверим являются ли  и
и  нулями
нулями  .
.
 .
.
После проверки нулем  является
является  .
.

Ответ:  .
.
17.  (*)
(*)
 ,
, 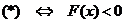

после проверки:  .
.


 .
.
Ответ:  .
.
18. 
Решение:

f(x) = sin3x, f2(x) =  , f3(x) =
, f3(x) = 
F(x) = f(x) f2(x) f3(x) Df = R

x1, x2 – нули функции, x3 – точки разрыва функции: k, n, l  Z
Z
т.к. F(x) > 0, когда 0 < x <  , то для F(x) на [0;
, то для F(x) на [0;  ] имеем
] имеем

Ответ:
