Теорема о существовании корня непрерывной функции.

Замечание.

Предел функции f(x) при 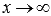бесконечен, если для любой бесконечно большой последовательности аргументов функции (бесконечно большой положительной или отрицательной), последовательность значений этой функции является бесконечно большой положительной или бесконечно большой отрицательной. Обозначается .

Вычисление пределов с помощью правила Лопиталя

Все вышеперечисленные пределы не использовали аппарат дифференциального исчисления. Однако, если необходимо найти

и при обе эти функции бесконечно малые или обе бесконечно большие, то их отношение не определено в точке и, следовательно, представляет собой неопределенность типа или соответственно. Поскольку это отношение в точке может иметь предел, конечный или бесконечный, то нахождение этого предела называется раскрытием неопределенности (правило Лопиталя Бернули),

и имеет место следующее равенство:

, если и .

1. (здесь имеет место неопределенность типа )=

= .

Аналогичное правило имеет место, если и , т.е. .

2. (неопределенность типа )

=

= .

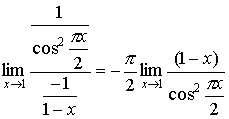
Правило Лопиталя позволяет также раскрывать неопределенности типа и . Для вычисления , где - бесконечно малая, а - бесконечно большая при (раскрытие неопределенности типа ) следует преобразовать произведение к виду

(неопределенность типа ) или к виду (неопределенность типа ) и далее использовать правило Лопиталя.

(проще см. лекцию)

13. Непрерывность функции в точке и на множестве. Непрерывность суммы, произведения и частного непрерывных функций; непрерывность сложной функции.

F(x) называется непрерывной в точке х₀ если выполняются три условия:

1) Она определена в точке х₀

2) Она имеет конечный предел в точке х₀

3) Lim f(x) = f(х₀) (x-- х₀₎

Функция , определённая на множестве 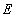, называется непрерывной на этом множестве, если она непрерывна в любой точке этого множества.

Теорема:

Сумма, произведение и частное двух непрерывных функций – непрерывны.

Доказательство:

Докажем для произведения.

Пусть 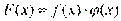. Тогда, по теореме о пределе произведения:

.

Теорема:

Пусть функция непрерывна в точке , а функция непрерывна в точке . Тогда сложная функция , состоящая из непрерывных функций, непрерывна в точке .

Доказательство:

Т.к. 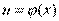- непрерывна, то , т.е. при имеем . Поэтом (т.к. - непрерывна) имеем: .

14. Точка разрыва функции; классификация точек разрыва.

Точка, в которой нарушается непрерывность функции, называется точкой разрыва этой функции.

Если хотя бы одно из равенств нарушается, говорят о разрыве в точке . Если и односторонние пределы конечны, то разрыв в точке называется устранимым. Если и оба односторонние пределы конечны, то говорят о скачке функции в точке . Устранимый разрыв и скачок называются разрывами первого рода. Если один из односторонних пределов бесконечен или не существует, то разрыв называется разрывом второго рода. Так же, как для предела и непрерывности, говорят о разрыве слева и разрыве справа.

15. Основные свойства непрерывных функций на отрезке.

теорема Вейерштрасса: если функция непрерывна на замкнутом промежутке [а, b], то она достигает на нём свои наименьшее и наибольшее значения. Искать эти значения надо либо на концах промежутка, либо в экстремальных (внутренних) точках.

Правило отыскания наибольшего и наименьшего значений функции f (х) на отрезке [ а, b ]:

1. Найти первую производную и все критические точки x_i, принадлежащие [ а, b ].
2. Вычислить значения f (x_i).
3. Вычислить значения функции на концах промежутка.
4. Сравнить все полученные значения функции f (x_i), f (a), f (b) и выбрать среди них самое большое и самое малое.

Теорема о существовании корня непрерывной функции.

Если функция непрерывна на отрезке и принимает на его концах значения разных знаков, то на этом отрезке существует по крайней мере один корень уравнения.

Теорема Коши (о промежуточных значениях непрерывной функции) пусть функция f(x) непрерывна на отрезке [a,b] и на концах этого отрезка принимает значения разных знаков, тогда найдется такая точка , в которой значение функции равно нулю.

(об ограниченности непрерывной функции) Пусть функция непрерывна на отрезке . Тогда ограничена на , то есть существует такая постоянная , что при всех .