Матрица линейного отображения

 

Определение

Определение 1. Пусть и — конечномерные векторные пространства над полем с базисами и соответственно. Рассмотрим линейное отображение . Тогда можно представить в виде для некоторых . Матрица называется матрицей линейного отображения ¹⁾ в базисах и . Столбцами этой матрицы являются координаты векторов в базисе .

Пусть произвольный вектор имеет следующие координаты в разложении по базису , , тогда его образ из пространства в базисе имеет разложение , где . То есть
.

Предложение 1. Существует взаимно однозначное отображение между множеством всех линейных отображений из -мерного векторного пространства в -мерное векторное пространство с фиксированными базисами и множеством матриц размера .

Определение 2. Матрица линейного оператора ²⁾ — это матрица линейного отображения в случае, когда .

Пример 1. Пусть — базис -мерного векторного пространства . Рассмотрим тождественный³⁾ линейный оператор . Так как , то матрица — это в точности единичная матрица
.

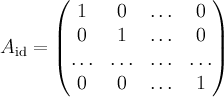Предложение 2. Пусть — конечномерные векторные пространства, и — линейные отображения. Тогда .

Умножением двух линейных операторов и 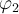на пространстве будем считать их композицию: . Тогда справедливо

Предложение 3. Пространство линейных операторов является ассоциативной алгеброй над полем . В случае, если пространство конечномерно, алгебра изоморфна алгебре всех матриц порядка над полем . Изоморфизм задается отображением .

 

4) Лине́йное отображе́ние, лине́йный опера́тор — обобщение линейной числовой функции (точнее, функции y = kx) на случай более общего множества аргументов и значений. Линейные операторы, в отличие от нелинейных, достаточно хорошо исследованы, что позволяет успешно применять результаты общей теории, так как их свойства не зависят от природы величин.

Лине́йным отображе́нием векторного пространства L_K над полем K в векторное пространство M_K (лине́йным опера́тором из L_K в M_K) над тем же полем K называется отображение

,

удовлетворяющее условию линейности

f (x + y) = f (x) + f (y),

f (α x) = α f (x).

для всех и .

 

Если определить операции сложения и умножения на скаляр из основного поля K как

§

§

множество всех линейных отображений из L_K в M_K превращается в векторное пространство, которое обычно обозначается как

[править]Важные частные случаи

§ Линейный функционал — линейный оператор, для которого M = K:

§ Эндоморфизм — линейный оператор, для которого L = M:

§ Тождественный оператор — оператор , отображающий каждый элемент пространства в себя.

§ Нулевой оператор — оператор, переводящий каждый элемент L_K в нулевой элемент M_K.

§ Проектор - оператор сопоставляющий каждому x его проекцию на подпространство.

§ Сопряжённый оператор к оператору — оператор A ^* на V ^*, заданный соотношением (A ^* f, x): = (f, Ax).

§ Самосопряжённый оператор — оператор, совпадающий со своим сопряжённым оператором. Иногда такие операторы называют гипермаксимальными эрмитовыми.

§ Эрмитов (или симметрический) оператор — такой оператор A, что (Ax, y) = (x, Ay) для всех пар x, y из области определения A. Для всюду определённых операторов совпадает с самосопряжённым.

§ Положительно определённый оператор. Пусть L_K, M_K - гильбертовы пространства. Тогда линейный оператор называется положительным, если .

[править]Связанные понятия

§ Образом подмножества^[1] относительно линейного отображения A называется множество .

§ Ядром линейного отображения называются подмножество A, которое отображается в нуль:

Ядро линейного отображения образует подпространство в линейном пространстве A.

§ Образом линейного отображения f называется следующее подмножество B:

Образ линейного отображения образует подпространство в линейном пространстве B.

§ Отображение прямого произведения линейных пространств A и B в линейное пространство C называется билинейным

, если оно линейно по обоим своим аргументам. Отображение прямого произведения большего числа линейных пространств называется полилинейным, если оно линейно по всем своим аргументам.

§ Оператор называется линейным неоднородным (или афинным), если он имеет вид

где L — линейный оператор, а v — вектор.

§ Пусть . Подпространство называется инвариантным относительно линейного отображения, если ^[2].

Критерий инвариантности. Пусть — подпространство,такое что X разлагается в прямую сумму: . Тогда M инвариантно относительно линейного отображения A тогда и только тогда, когда P_MAP_M = AP_M, где P_M - проектор на подпространство M.

§ Фактор-операторы ^[3]. Пусть — линейный оператор и пусть M — некоторое инвариантное относительно этого оператора подпространство. Образуем фактор-пространство по подпространству M. Тогда фактор-оператором называется оператор A ⁺ действующий на по правилу: , где [ Ax ] -- класс из фактор-пространства, содержащий Ax.

[править]Примеры

Примеры линейных однородных операторов:

§ оператор дифференцирования: ;

§ оператор интегрирования: ;

§ оператор умножения на определённую функцию φ(t): y (t) = φ(t) x (t);

§ оператор интегрирования с заданным «весом»

§ оператор взятия значения функции f в конкретной точке x ₀: L { f } = f (x ₀)^[4];

§ оператор умножения вектора на матрицу: b = Ax;

§ оператор поворота вектора.

Примеры линейных неоднородных операторов:

§ Любое аффинное преобразование;

§ ;

§ ;

§ y (t) = φ₁(t) x (t) + φ₂(t);

где φ(t), φ₁(t), φ₂(t) — вполне определённые функции, а x (t) — преобразуемая оператором функция.

 

5) Норма вектора.
Для векторов есть мерило их отличия друг от друга. Это - норма (модуль) разности векторов.
Норму вектора определяют многими разными способами. В рамках нашей теории все они должны обладать следующими свойствами:
	(5.01)
Здесь в первом свойстве фигурируют норма (модуль) вектора X и абсолютная величина (модуль) числа a. Третье свойство называют неравенством треугольника за его геометрический смысл (длина стороны треугольника не превосходит суммы длин двух других сторон). На втором свойстве держится возможность определить предел X последовательности векторов Xn не покоординатным способом(т.е. координаты предельного вектора определять как пределы координат векторов Xn), а с помощью рассмотрения нормы разницы между векторами Xn и предельным вектором X:
	(5.02)
Самые популярные способы определить норму вектора, - это следующие два:
	(5.03)
	(5.04)
В (5.03) нормой вектора объявляют наибольший из модулей его координат. Формулу |X-Y| расстояния между точками X и Y (у нас столбцы X,Y можно по необходимости рассматривать либо как точки либо как радиус-векторы), построенную на основе такой нормы, называют равномерной метрикой. Поэтому и эту норму мы будем называть равномерной нормой.
	У читателя наверняка возникнет вопрос о происхождении названия. Разумеется, оно связано с понятием равномерной сходимости последовательности функций, знакомое студенту из математического анализа. Если рассмотреть координаты векторов Xn как функции двух аргументов x (k, n) (здесь n - номер вектора, k - номер его координаты), то сходимость (5.02) по равномерной норме (5.03) означает сходимость последовательности функций f n(k) = x (k, n) к функции x (k), равномерную по аргументу k. Почему это так? Потому что неравенство
	равносильно требованию, чтобы неравенства
	выполнялись сразу для всех k, то есть равномерно по k.
	Важно заметить, что в равномерной норме окрестность точки X0 радиуса R (т.е.множество точек X удаленных от X0 на расстояние, меньшее R) имеет форму n-мерного куба с центром в точке X0 и ребрами длиной 2R, параллельными осям координат. В частности, в двумерном пространстве это квадрат. Сфера радиуса R в этой норме является поверхностью куба (в двумерном случае - границей квадрата).
Вторая норма (5.04) порождена известной всем теоремой Пифагора. Обычно эту норму называют Евклидовой, потому что, задавшись ею как средством измерения расстояния между "бесконечно"близкими точками пространства (в дифференциальной геометрии), мы получим в качестве кратчайших путей Евклидовы прямые; получим также и все факты Евклидовой геометрии. Иногда эту норму называют энергетической, когда в прикладных задачах она связана с энергией (например, потенциальная энергия малой деформации нескольких пружин выражается через сумму квадратов их удлинений).
Возникает естественный вопрос: какая из норм лучше?
Для конечномерных векторов X эти нормы топологически эквивалентны в следующем смысле: для окрестности {X: |X-X0| < R} любого радиуса R любой точки X0 построенной на основе одной из норм, можно построить вписанную в нее и описанную вокруг нее окрестности, построенные на основе другой нормы (разумеется, другого радиуса). Рисунок показывает, что нормы (5.02) и (5.03) в двумерном пространстве таким свойством обладают.
Эквивалентность норм дает нам следующее. Если на основе определения (5.02), используя одну из этих норм, удалось установить, что lim Xn = X, то то же самое можно доказать и с использованием другой, эквивалентной ей нормы.
В нашем случае норм (5.03), (5.04) это означает, что в конечномерном пространстве сходимость по энергетической норме равноценна равномерной сходимости, то есть покоординатной. Поэтому мы можем для предельных переходов в теоремах выбирать ту из этих двух норм, в которой выкладки проще.
	Мы должны заметить, что для бесконечномерных векторов нет эквивалентности этих норм. Действительно: диагональ единичного куба, вычисленная по формуле (5.04) с бесконечным числом слагаемых, является бесконечно большой. Поэтому вокруг такого куба описать Евклидову сферу невозможно. В результате получается, что равномерная норма оказывается сильнее. Из сходимости в равномерной норме следует сходимость в энергетической, обратное неверно (обратное верно в конечномерном случае). Поскольку функции f(x) в математике часто рассматривают как бесконечномерные векторы, сказанное в полной мере относится к последовательностям функций.